CMPT 225 Binary Search Trees Trees l A

CMPT 225 Binary Search Trees

Trees l A set of nodes with a single starting point l l l Each node is connected by an edge to some other node A tree is a connected graph l l There is a path to every node in the tree There are no cycles in the tree. l l called the root It can be proved by MI that a tree has one less edge than the number of nodes. Usually depicted with the root at the top

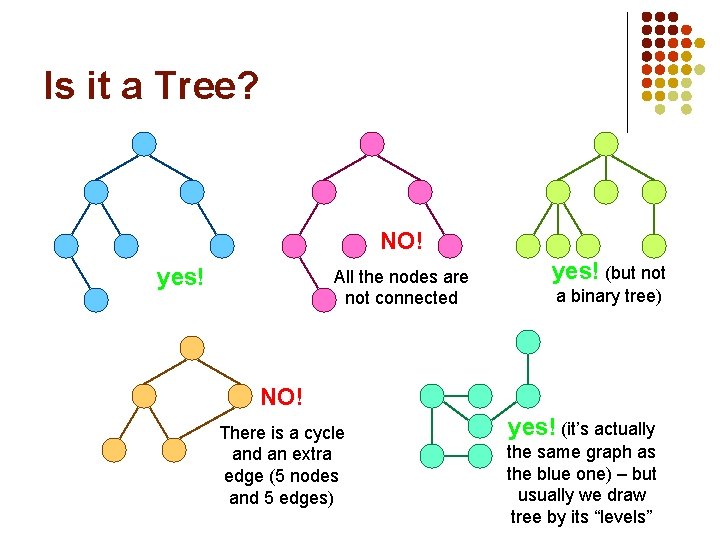
Is it a Tree? NO! yes! All the nodes are not connected yes! (but not a binary tree) NO! There is a cycle and an extra edge (5 nodes and 5 edges) yes! (it’s actually the same graph as the blue one) – but usually we draw tree by its “levels”

Examples of trees l l directory structure family trees: l l all descendants of a particular person all ancestors born after year 1800 of a particular person evolutionary tress (also called phylogenetic trees) albegraic expressions

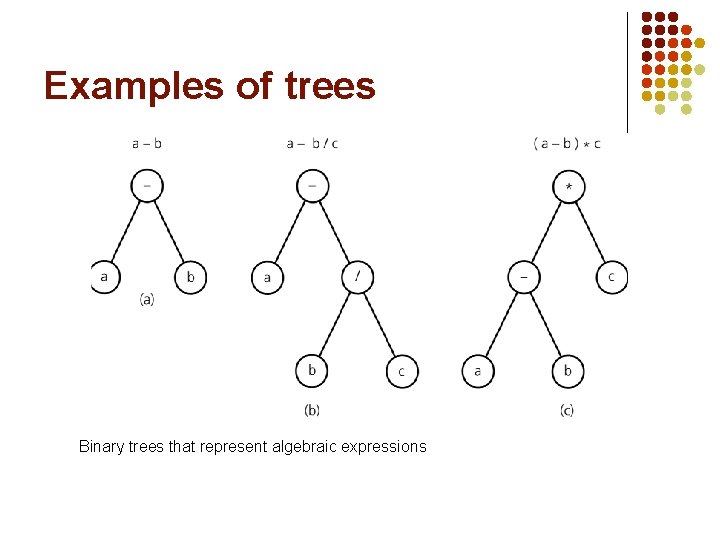
Examples of trees Binary trees that represent algebraic expressions

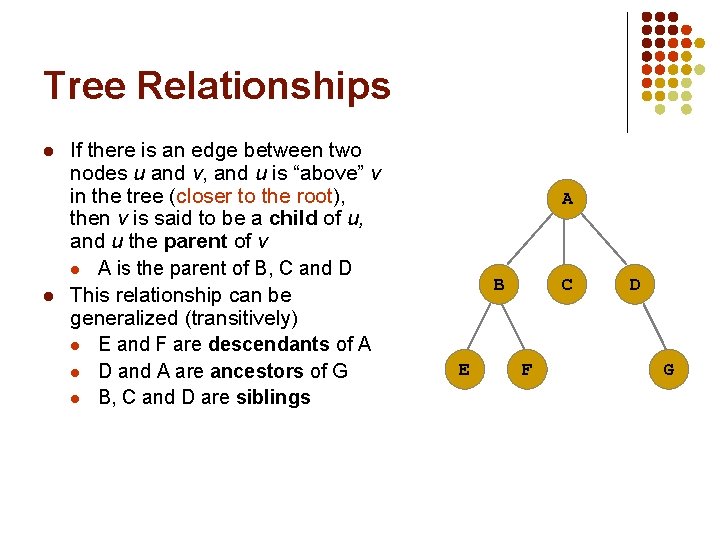
Tree Relationships l l If there is an edge between two nodes u and v, and u is “above” v in the tree (closer to the root), then v is said to be a child of u, and u the parent of v l A is the parent of B, C and D This relationship can be generalized (transitively) l E and F are descendants of A l D and A are ancestors of G l B, C and D are siblings A B E C F D G

More Tree Terminology l l A leaf is a node with no children A path [a branch] is a sequence of nodes v 1 … vn l l l where vi is a parent of vi+1 (1 i n-1) [and v 1 is a root and vn is a leaf] A subtree is any node in the tree along with all of its descendants A binary tree is a tree with at most two children per node l l The children are referred to as left and right (i. e. , children are usually ordered) We can also refer to left and right subtrees of a node

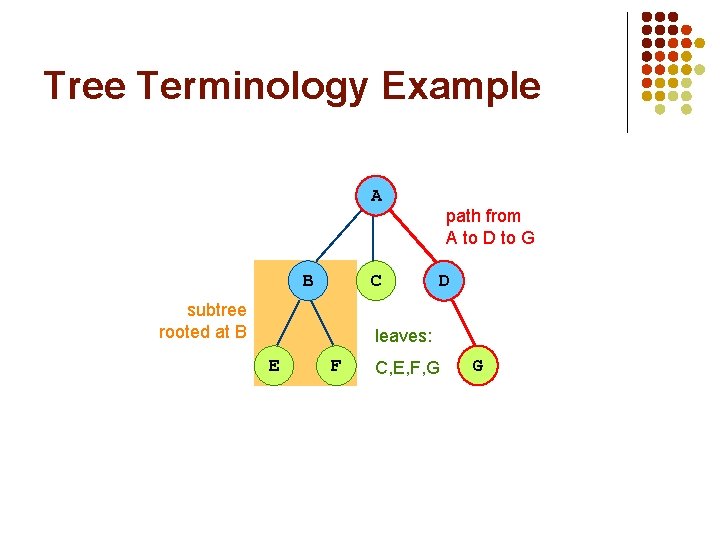
Tree Terminology Example A C B subtree rooted at B path from A to D to G D leaves: E F C, E, F, G G

Binary Tree A B left subtree of A D C right child of A E F G right subtree of C H I J

Measuring Trees l The height of a node v is the number of nodes on the longest path from v to a leaf l l The depth of a node v is the number of nodes on the path from the root to v l l The height of the tree is the height of the root, which is the number of nodes on the longest path from the root to a leaf This is also referred to as the level of a node Note that there are slightly different formulations of the height of a tree l Where the height of a tree is said to be the length (the number of edges) on the longest path from node to a leaf

Height of a Binary Tree A height of node B is 3 D height of the tree is 4 B C E F level 2 G level 3 depth of node E is 3 H I J level 4

Representation of binary trees public class Tree. Node<T> { private T item; private Tree. Node<T> left. Child; private Tree. Node<T> right. Child; public Tree. Node(T new. Item) { // Initializes tree node with item and no children (a leaf). item = new. Item; left. Child = null; right. Child = null; } // end constructor public Tree. Node(T new. Item, Tree. Node<T> left, Tree. Node<T> right) { // Initializes tree node with item and // the left and right children references. item = new. Item; left. Child = left; right. Child = right; } // end constructor public T get. Item() { // Returns the item field. return item; } // end get. Item

public void set. Item(T new. Item) { // Sets the item field to the new value new. Item. item = new. Item; } // end set. Item public Tree. Node<T> get. Left() { // Returns the reference to the left child. return left. Child; } // end get. Left public void set. Left(Tree. Node<T> left) { // Sets the left child reference to left. Child = left; } // end set. Left public Tree. Node<T> get. Right() { // Returns the reference to the right child. return right. Child; } // end get. Right public void set. Right(Tree. Node<T> right) { // Sets the right child reference to right. Child = right; } // end set. Right } // end Tree. Node

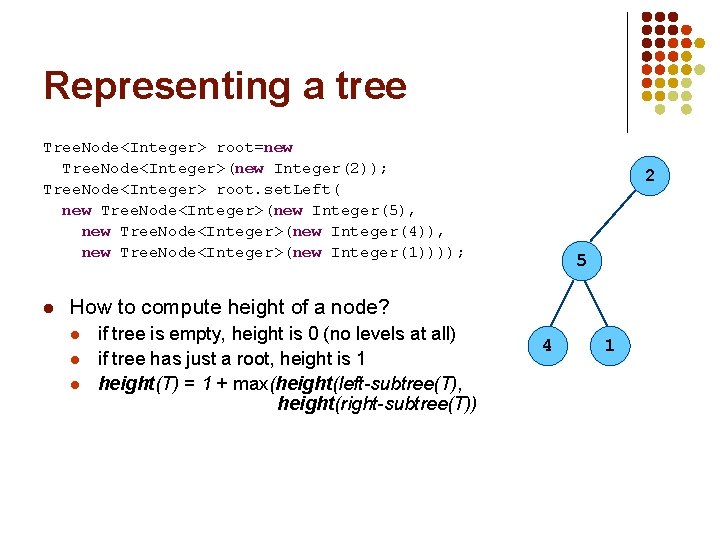
Representing a tree Tree. Node<Integer> root=new Tree. Node<Integer>(new Integer(2)); Tree. Node<Integer> root. set. Left( new Tree. Node<Integer>(new Integer(5), new Tree. Node<Integer>(new Integer(4)), new Tree. Node<Integer>(new Integer(1)))); l 2 5 How to compute height of a node? l l l if tree is empty, height is 0 (no levels at all) if tree has just a root, height is 1 height(T) = 1 + max(height(left-subtree(T), height(right-subtree(T)) 4 1

Special types of Binary Trees l A binary tree is full if no node has only one child and if all the leaves have the same depth l l A complete binary tree is one where l l A full binary tree of height h has (2 h – 1) nodes, of which 2 h-1 are leaves The leaves are on at most two different levels, The second to bottom level is filled in and The leaves on the bottom level are as far to the left as possible. A balanced binary tree is one where l No leaf is more than a certain amount farther from the root than any other leaf, this is sometimes stated more specifically as: l l The height of any node’s right subtree is at most one different from the height of its left subtree A balanced tree’s height is sometime specified in terms of its relation to the number of nodes in the tree (see red-black trees)

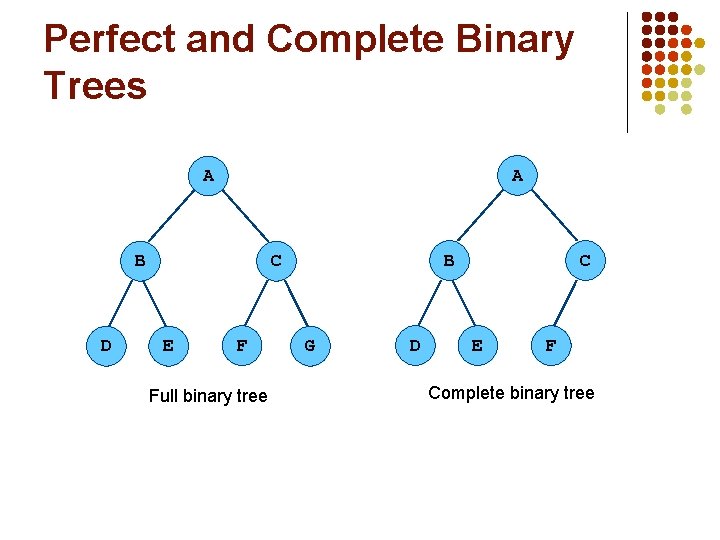
Perfect and Complete Binary Trees A A B D B C E F Full binary tree G D C E F Complete binary tree

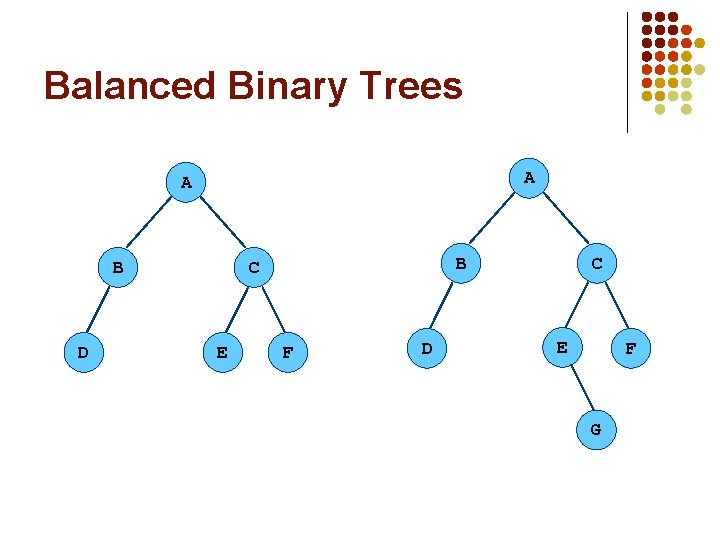
Balanced Binary Trees A A B D B C E F D C E F G

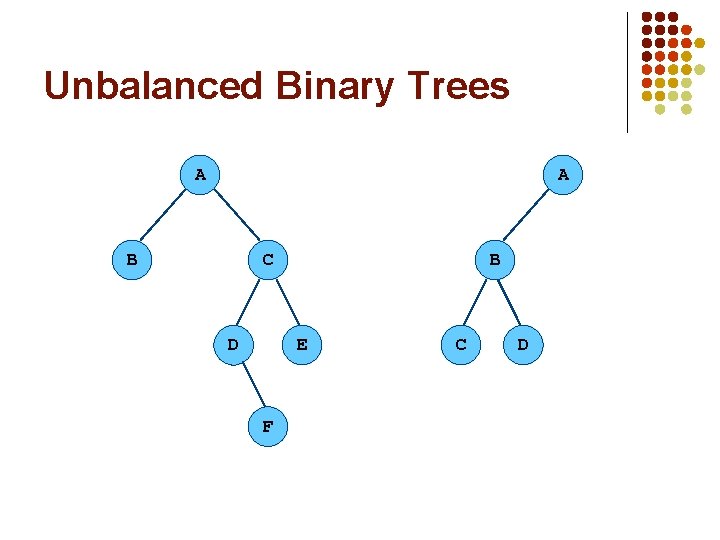
Unbalanced Binary Trees A A B C B E D F C D

Binary Tree Traversals l A traversal algorithm for a binary tree visits each node in the tree l l l and, typically, does something while visiting each node! Traversal algorithms are naturally recursive There are three traversal methods l l l Inorder Preorder Postorder

In. Order Traversal Algorithm // In. Order traversal algorithm in. Order(Tree. Node<T> n) { if (n != null) { in. Order(n. get. Left()); visit(n) in. Order(n. get. Right()); } }

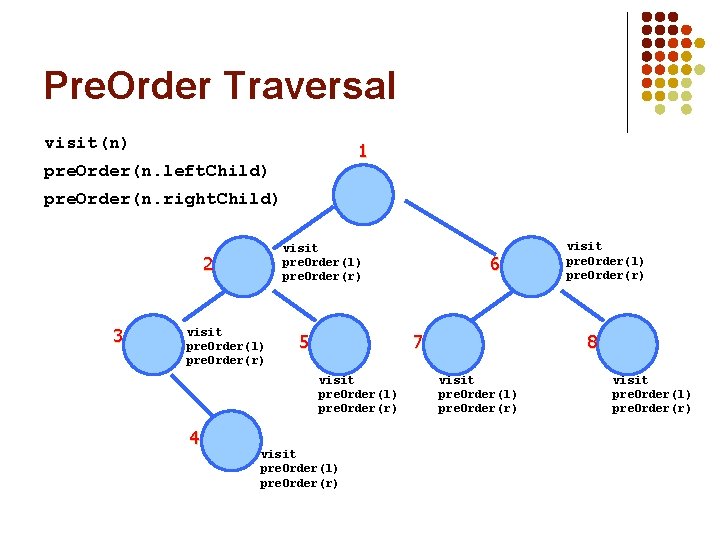
Pre. Order Traversal visit(n) 1 pre. Order(n. left. Child) 17 pre. Order(n. right. Child) 2 3 9 13 visit pre. Order(l) pre. Order(r) 5 16 visit pre. Order(l) pre. Order(r) 4 11 visit pre. Order(l) pre. Order(r) 6 7 20 visit pre. Order(l) pre. Order(r) 27 visit pre. Order(l) pre. Order(r) 8 39 visit pre. Order(l) pre. Order(r)

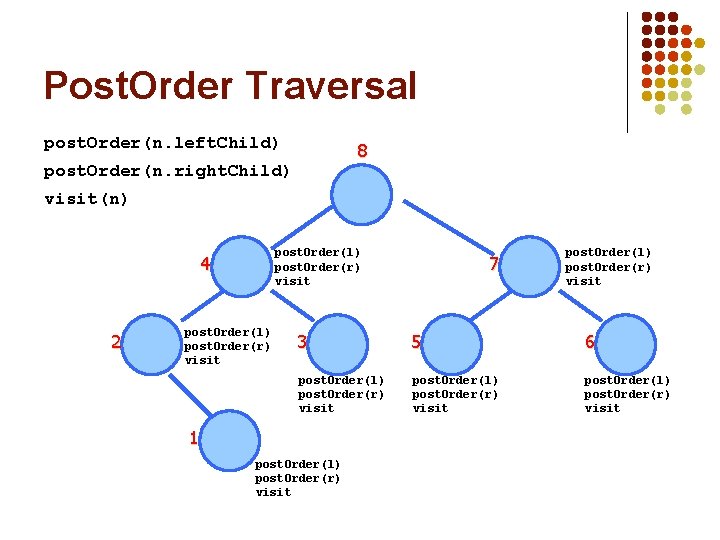
Post. Order Traversal post. Order(n. left. Child) 8 post. Order(n. right. Child) 17 visit(n) 4 2 9 13 post. Order(l) post. Order(r) visit 3 16 post. Order(l) post. Order(r) visit 1 11 post. Order(l) post. Order(r) visit 7 5 20 post. Order(l) post. Order(r) visit 27 post. Order(l) post. Order(r) visit 6 39 post. Order(l) post. Order(r) visit