CMPS 256 Advanced Algorithms and Data Structures Growth

CMPS 256: Advanced Algorithms and Data Structures Growth of Functions

Credits Slides based on: • Monica Nicolescu @ UNR • F. Abu Salem, J. Boulos, W. Keyrouz, & George Turkiyyah @ AUB 2

Algorithm Analysis • The amount of resources used by the algorithm – Space – Computational time • Running time: – The number of primitive operations (steps) executed before termination • Order of growth – The leading term of a formula – Expresses the behavior of a function toward infinity 3

Runtime Analysis • In this course, we will typically use T(n) to refer to worst-case running time, unless otherwise noted • It is difficult to determine T(n) experimentally – Too many possible inputs – Don’t know a priori which input leads to worst-case behavior • We will instead determine T(n) theoretically- by analyzing/counting number of primitive operations in algorithm pseudocode 4

Order of growth • Alg. : MIN (a[1], …, a[n]) m ← a[1]; for i ← 2 to n if a[i] < m then m ← a[i]; • Running time: T(n) =1 [first step] + (n) [for loop] + (n-1) [if condition] + (n-1) [the assignment in then] = 3 n - 1 • Order (rate) of growth: – The leading term of the formula – Gives a simple characterization of the algorithm’s efficiency – Expresses the asymptotic behavior of the algorithm • T(n) grows like n 5

Analyzing Code • Conditional statements if C then S 1 else S 2 time(C) + Max( time(S 1), time(S 2)) • Loops for i a 1 to a 2 do S time(Si) for all i 6

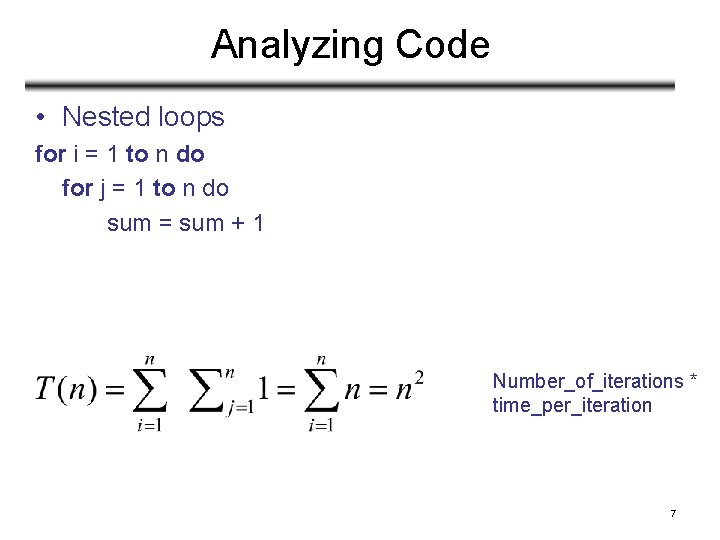
Analyzing Code • Nested loops for i = 1 to n do for j = 1 to n do sum = sum + 1 Number_of_iterations * time_per_iteration 7

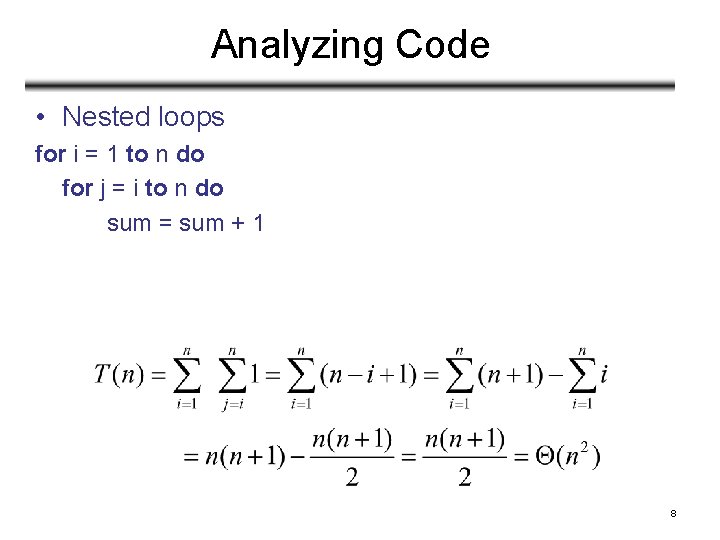
Analyzing Code • Nested loops for i = 1 to n do for j = i to n do sum = sum + 1 8

Exercise • A more complicated example for ( i=0; i<=n 2; i++) for ( j=i; j>=1; j= j/5 ) sum = sum + 1 T(n) = ? 9

Typical Running Time Functions • 1 (constant running time): – Instructions are executed once or a few times • log. N (logarithmic) – A big problem is solved by cutting the original problem in smaller sizes, by a constant fraction at each step • N (linear) – A small amount of processing is done on each input element • N log. N (log-linear)s – A problem is solved by dividing it into smaller problems, solving them independently and combining the solution 10

Typical Running Time Functions • N(1+c) where c is a constant satisfying 0 < c < 1 (super-linear) • N 2 (quadratic) – Typical for algorithms that process all pairs of data items (double nested loops) • N 3 (cubic) – Processing of triples of data (triple nested loops) • NK (polynomial) • k. N (exponential) – Few exponential algorithms are appropriate for practical use 11

Logarithms • In algorithm analysis we often use the notation “log n” without specifying the base Binary logarithm Natural logarithm 12

Some Common Functions • Floors and ceilings – x : the greatest integer less than or equal to x – x : the least integer greater than or equal to x – 1 < x ≤ x < x + 1 13

Some Simple Summation Formulas • Arithmetic series: • Geometric series: – Special case: x < 1: • Harmonic series: • Other important formulae: 14

Mathematical Induction • Used to prove a sequence of statements (S(1), S(2), … S(n)) indexed by positive integers • Proof: – Basis step: prove that the statement is true for n = 1 – Inductive step: assume that S(n) is true and prove that S(n+1) is true for all n ≥ 1 • The key to mathematical induction is to find case n “within” case n+1 15

Example • Prove that: 2 n + 1 ≤ 2 n for all n ≥ 3 • Basis step: – n = 3: • 2 3 + 1 ≤ 23 7 ≤ 8 TRUE Inductive step: – Assume inequality is true for n, and prove it for (n+1): 2 n + 1 ≤ 2 n must prove: 2(n + 1) + 1 ≤ 2 n+1 2(n + 1) + 1 = (2 n + 1 ) + 2 ≤ 2 n + 2 (by induction) 2 n + 2 n = 2 n+1 (2 ≤ 2 n for n ≥ 1) 16

Another Example • Prove that: • Basis step: – n = 1: • Inductive step: – Assume inequality is true for n, and prove it is true for (n+1): – Assume and prove: 17

Asymptotic Notations • A way to describe behavior of functions in the limit – How we indicate running times of algorithms – Describe the running time of an algorithm as n grows to • O notation: asymptotic “less than”: f(n) “≤” g(n) • notation: asymptotic “greater than”: f(n) “≥” g(n) • notation: asymptotic “equality”: f(n) “=” g(n) 18

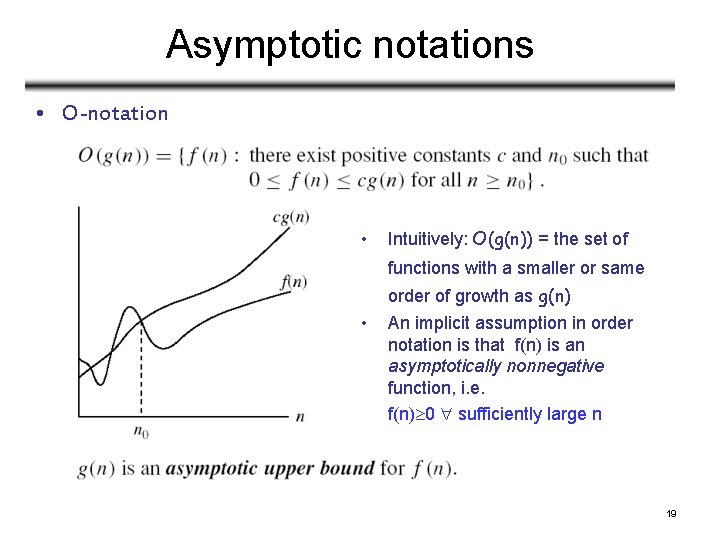
Asymptotic notations • O-notation • Intuitively: O(g(n)) = the set of functions with a smaller or same order of growth as g(n) • An implicit assumption in order notation is that f(n) is an asymptotically nonnegative function, i. e. f(n) 0 sufficiently large n 19

Examples – 2 n 2 = O(n 3): 2 n 2 ≤ cn 3 2 ≤ cn possibly c = 1 and n 0= 2 – n 2 = O(n 2): n 2 ≤ cn 2 c ≥ 1 possibly c = 1 and n 0= 1 – 1000 n 2+1000 n = O(n 2): 1000 n 2+1000 n ≤ cn 2+ 1000 n possibly c=1001 and n 0 = 1000 2 – n = O(n 2): n ≤ cn ≥ 1 possibly c = 1 and n 0= 1 20

Examples • E. g. : prove that n 2 ≠ O(n) – Assume c & n 0 such that: n≥ n 0: n 2 ≤ cn – Choose n = max (n 0, c) – n 2 = n n ≥ n c n 2 ≥ cn contradiction!!! 21

Comments • Our textbook uses “asymptotic notation” and “order notation” interchangeably • Order notation can be interpreted in terms of set membership, for e. g. , – T(n) = O(f(n)) is equivalent to T(n) O(f(n)) – O(f(n)) is said to be “the set of all functions for which f(n) is an upper bound” 22

Asymptotic notations (cont. ) • - notation • Intuitively: (g(n)) = the set of functions with a larger or same order of growth as g(n) 23

Examples – 5 n 2 = (n) 2 c, n 0 such that: 0 cn 5 n 2 Possibly c = 1 and n 0 = 1 – 100 n + 5 ≠ (n 2) Spse c, n 0 such that: 0 cn 2 100 n + 5 n ( n 1) = 105 n cn 2 105 n n(cn – 105) 0 Since n is positive cn – 105 0 n 105/c contradiction: n cannot be smaller than a constant – n = (2 n), n 3 = (n 2), n = (logn) 24

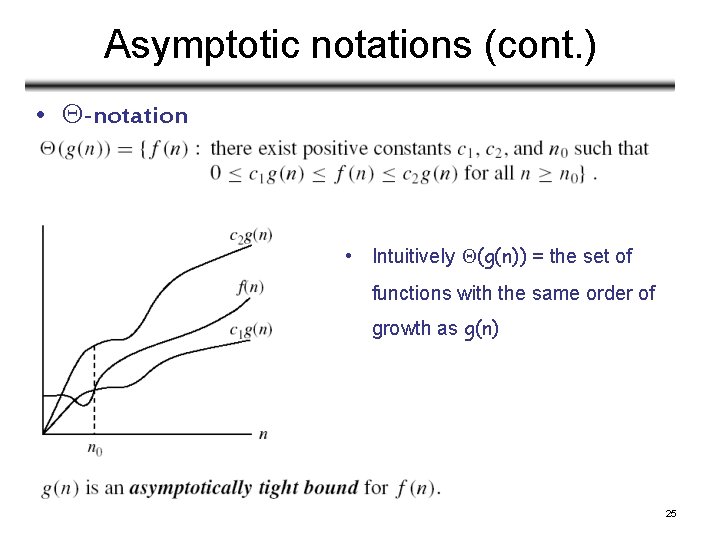
Asymptotic notations (cont. ) • -notation • Intuitively (g(n)) = the set of functions with the same order of growth as g(n) 25

Examples – n 2/2 –n/2 = (n 2) • ½ n 2 - ½ n ≤ ½ n 2 n ≥ 0 c 2= ½ • ½ n 2 - ½ n ≥ ½ n 2 - ½ n * ½ n ( n ≥ 2 ) = ¼ n 2 c 1= ¼ – n ≠ (n 2): c 1 n 2 ≤ n ≤ c 2 n 2 only holds for: n ≤ 1/c 1 – 6 n 3 ≠ (n 2): c 1 n 2 ≤ 6 n 3 ≤ c 2 n 2 only holds for: n ≤ c 2 /6 – n ≠ (logn): c 1 logn ≤ c 2 logn c 2 ≥ n/logn, n≥ n 0 – impossible 26

More on Asymptotic Notations • There is no unique set of values for n 0 and c in proving the asymptotic bounds • Prove that 100 n + 5 = O(n 2) – 100 n + 5 ≤ 100 n + n = 101 n ≤ 101 n 2 for all n ≥ 5 n 0 = 5 and c = 101 is a solution – 100 n + 5 ≤ 100 n + 5 n = 105 n ≤ 105 n 2 for all n ≥ 1 n 0 = 1 and c = 105 is also a solution Must find SOME constants c and n 0 that satisfy the asymptotic notation relation 27

Asymptotic Notations - Examples • notation – n 2/2 – n/2 = (n 2) – (6 n 3 + 1)lgn/(n + 1) = (n 2 lgn) – n vs. n 2 n ≠ (n 2) • notation • O notation – n vs. 2 n n = (2 n) – 2 n 2 vs. n 3 2 n 2 = O(n 3) – n 3 vs. n 2 n 3 = (n 2) – n 2 vs. n 2 = O(n 2) – n vs. logn n = (logn) – n 3 vs. nlogn n 3 O(nlgn) – n vs. n 2 n (n 2) 28

Comparisons of Functions • Theorem: f(n) = (g(n)) f = O(g(n)) and f = (g(n)) • Transitivity: – f(n) = (g(n)) and g(n) = (h(n)) f(n) = (h(n)) – Same for O and • Reflexivity: – f(n) = (f(n)) – Same for O and • Symmetry: – f(n) = (g(n)) if and only if g(n) = (f(n)) • Transpose symmetry: – f(n) = O(g(n)) if and only if g(n) = (f(n)) 29

Asymptotic Notations - Examples • For each of the following pairs of functions, either f(n) is O(g(n)), f(n) is Ω(g(n)), or f(n) = Θ(g(n)). Determine which relationship is correct. f(n) = (g(n)) – f(n) = log n 2; g(n) = log n + 5 – f(n) = n; g(n) = log n 2 f(n) = (g(n)) – f(n) = log n; g(n) = log n f(n) = O(g(n)) – f(n) = n; g(n) = log 2 n f(n) = (g(n)) – f(n) = n log n + n; g(n) = log n f(n) = (g(n)) – f(n) = 10; g(n) = log 10 f(n) = (g(n)) – f(n) = 2 n; g(n) = 10 n 2 f(n) = (g(n)) – f(n) = 2 n; g(n) = 3 n f(n) = O(g(n)) 30

Asymptotic Notations in Equations • On the right-hand side – (n 2) stands for some anonymous function in (n 2) 2 n 2 + 3 n + 1 = 2 n 2 + (n) means: There exists a function f(n) with the desired properties such that 2 n 2 + 3 n + 1 = 2 n 2 + f(n) • On the left-hand side 2 n 2 + (n) = (n 2) No matter how the anonymous function is chosen on the left-hand side, there is a way to choose the anonymous function on the right-hand side to make the equation valid. 31

Limits and Comparisons of Functions Using limits for comparing orders of growth: • compare ½ n (n-1) and n 2 32

Limits and Comparisons of Functions L’Hopital rule: • compare lgn and 33

Some Common Functions • Factorials Stirling’s approximation 34

Exercises • Is this true: f(n)=O(g(n)) f(n)+g(n)= (f(n)) If so, give a proof that uses formal definition of O, , and • Order these functions asymptotically from slowest to fastest: 35