CMOS SwitchedCapacitor Circuits for BioMedical and RF Applications

CMOS Switched-Capacitor Circuits for Bio-Medical and RF Applications David J. Allstot Mackay Professor of EECS University of California Berkeley, CA 94720

Origin of Switched-Capacitors? James C. Maxwell, A Treatise on Electricity and Magnetism Oxford: Clarendon Press, 1873, vol. 2, pp. 374 -375. 2

MOS Switched Capacitors - 1972 • David L. Fried, “Analog Sample-Data Filters, ” IEEE J. Solid-State Circuits, pp. 302 -304, Aug. 1972. – MOS SC “resistor” concept and SC n-path filter Early MOS data converters and switched-capacitor filters for the perchannel voice-to-PCM interface of digital telephony – UC Berkeley Paul R. Gray • J. L. Mc. Creary and P. R. Gray, “All-MOS charge redistribution analog-todigital conversion techniques: Part I, ” IEEE JSSC, Dec. 1975. • R. E. Suarez, P. R. Gray and D. A. Hodges, “All-MOS charge redistribution analog-to-digital conversion techniques: Part II, ” IEEE JSSC, Dec. 1975. • Y. P. Tsividis and P. R. Gray, “An integrated NMOS operational amplifier with internal compensation, ” IEEE JSSC, Dec. 1976. David A. Hodges • I. A. Young, D. A. Hodges and P. R. Gray, “Analog NMOS sampled-data recursive filter, ” IEEE ISSCC, Feb. 1977. • D. J. Allstot, R. W. Brodersen and P. R. Gray, “MOS switched-capacitor ladder filters, ” IEEE JSSC, Dec. 1978. Key Paper on n-path filter analysis: • Robert W. Brodersen B. D. Smith, “Analysis of commutated networks, ” IRE Trans. on Aerospace and Navigational Electronics, pp. 21 -26, 1953. 3

Future Research Topics N-Path Filters: Blocker-tolerant front ends Switched Capacitor: High-efficiency, high-power transmitters; Converters Time-to-Digital Converter: Ring-oscillator amplifiers; Analog-to-digital converters Golden Age for RF-CMOS Design! *Courtesy of Prof. James Buckwalter, UC Santa Barbara 4

Outline § Challenges in CMOS Radio Design § Switched-Capacitor N-path Filters § Analog-domain Compressed Sensing for Bio-signal Acquisition 5

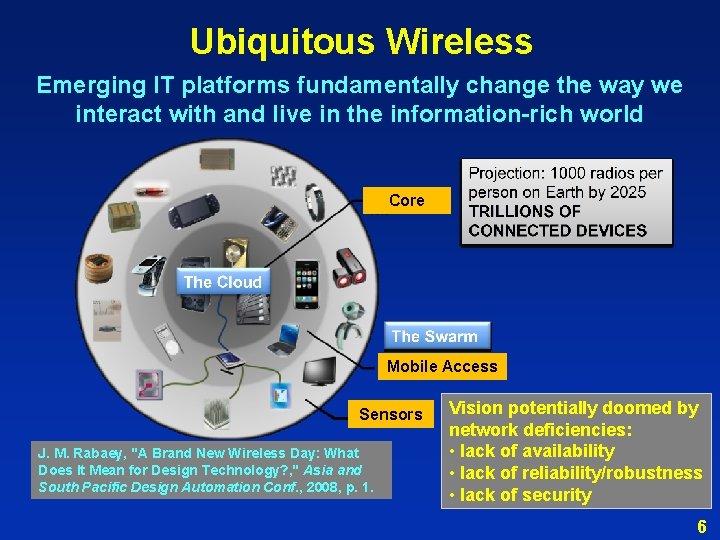
Ubiquitous Wireless Emerging IT platforms fundamentally change the way we interact with and live in the information-rich world Core Mobile Access Sensors J. M. Rabaey, "A Brand New Wireless Day: What Does It Mean for Design Technology? , " Asia and South Pacific Design Automation Conf. , 2008, p. 1. Vision potentially doomed by network deficiencies: • lack of availability • lack of reliability/robustness • lack of security 6

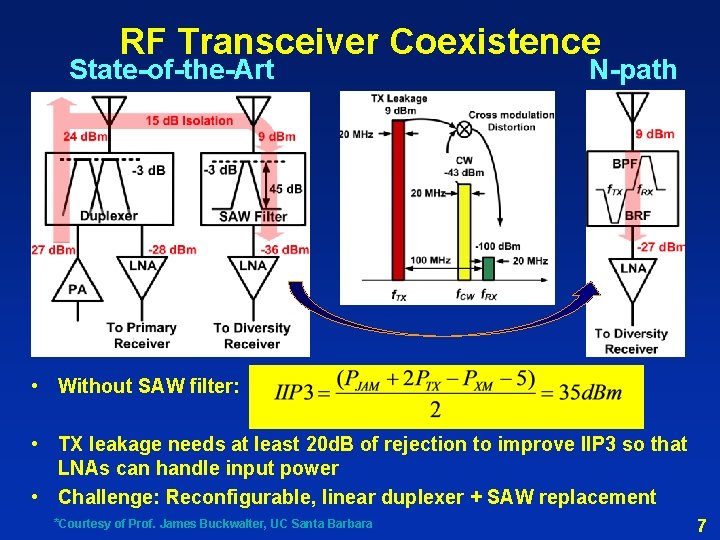
RF Transceiver Coexistence State-of-the-Art N-path • Without SAW filter: • TX leakage needs at least 20 d. B of rejection to improve IIP 3 so that LNAs can handle input power • Challenge: Reconfigurable, linear duplexer + SAW replacement *Courtesy of Prof. James Buckwalter, UC Santa Barbara 7

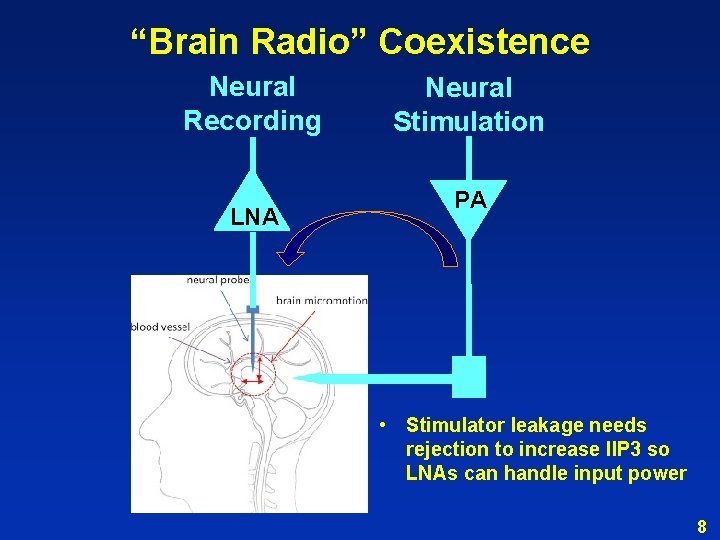
“Brain Radio” Coexistence Neural Recording LNA Neural Stimulation PA • Stimulator leakage needs rejection to increase IIP 3 so LNAs can handle input power 8

Universal Receiver – Blocker Rejection • Low Cost - No Inductors - No Off-Chip Filters • • Low Noise Figure • • High Linearity • • Low Power Diss. • • High Blocker Tolerance • • Wide Frequency Range GSM Example *Courtesy of Prof. Behzad Razavi, UCLA, 2015 ISCAS Keynote Presentation 9

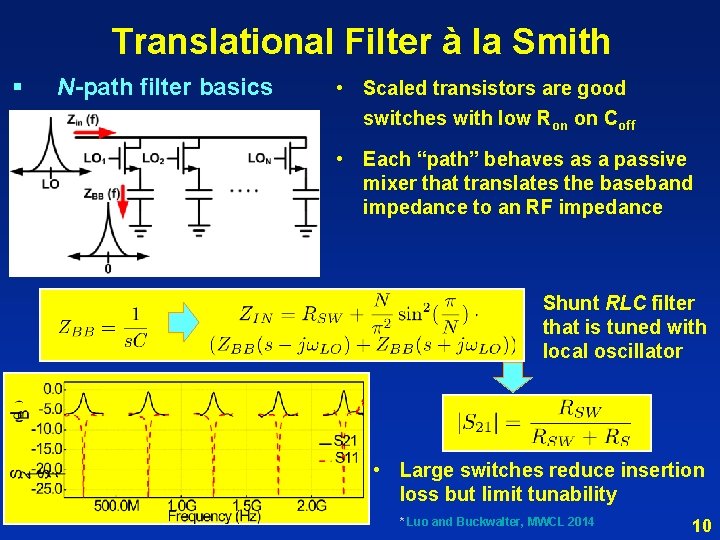
Translational Filter à la Smith § N-path filter basics • Scaled transistors are good switches with low Ron on Coff • Each “path” behaves as a passive mixer that translates the baseband impedance to an RF impedance Shunt RLC filter that is tuned with local oscillator • Large switches reduce insertion loss but limit tunability * Luo and Buckwalter, MWCL 2014 10

Shunt vs. Series N-path Filters • Shunt filter: Bandpass response • Series filter: Bandreject response • compatible with digital CMOS • Benefits from faster switches (e. g. , CMOS SOI process) * Luo and Buckwalter, MWCL 2014 11

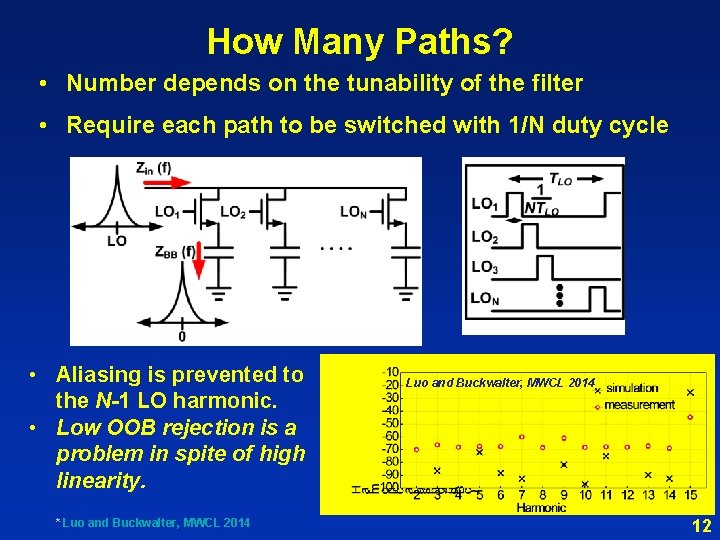
How Many Paths? • Number depends on the tunability of the filter • Require each path to be switched with 1/N duty cycle • Aliasing is prevented to the N-1 LO harmonic. • Low OOB rejection is a problem in spite of high linearity. * Luo and Buckwalter, MWCL 2014 12

Can We Filter at the Antenna? § N-path filter basics • For BW = 200 k. Hz: Ctot = 28 n. F • For 20 -d. B rejection: Rsw = 5 W • Switch linearity with 0 -d. Bm blocker? *Courtesy of Prof. Behzad Razavi, UCLA, 2015 ISCAS Keynote Presentation 13

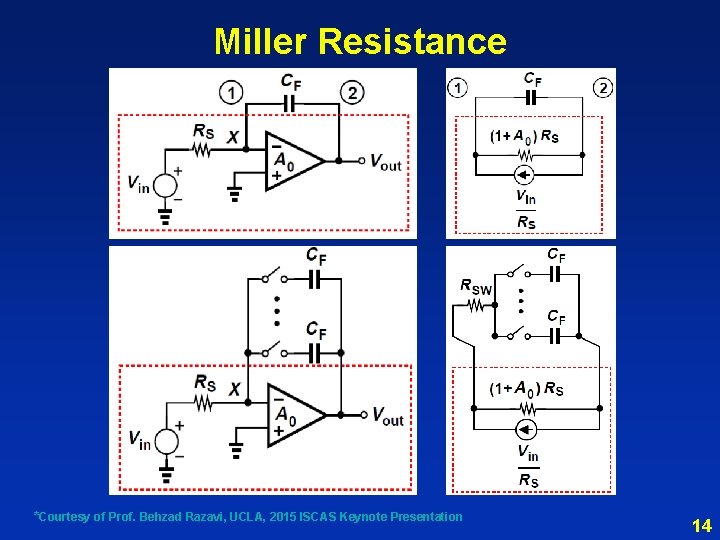
Miller Resistance *Courtesy of Prof. Behzad Razavi, UCLA, 2015 ISCAS Keynote Presentation 14

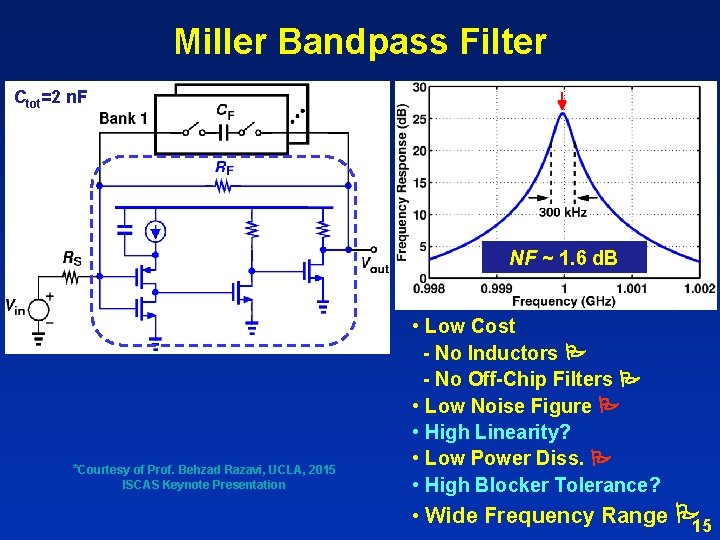
Miller Bandpass Filter Ctot=2 n. F NF ~ 1. 6 d. B *Courtesy of Prof. Behzad Razavi, UCLA, 2015 ISCAS Keynote Presentation • Low Cost - No Inductors - No Off-Chip Filters • Low Noise Figure • High Linearity? • Low Power Diss. • High Blocker Tolerance? • Wide Frequency Range 15

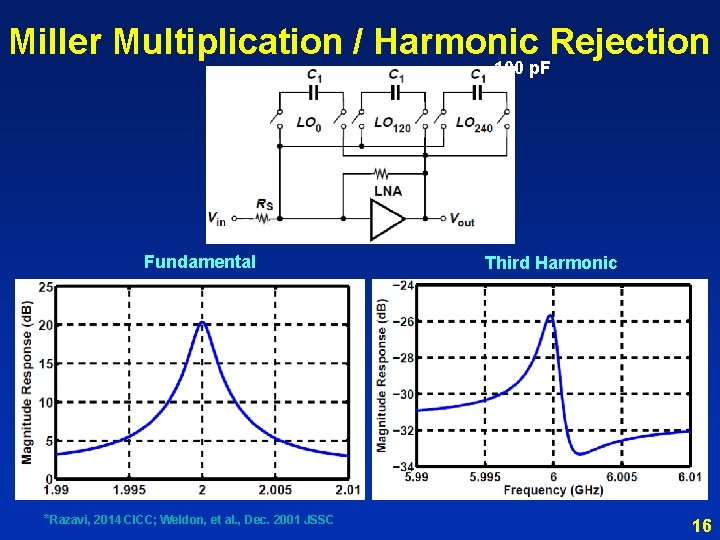
Miller Multiplication / Harmonic Rejection 100 p. F 50 W Fundamental *Razavi, 2014 CICC; Weldon, et al. , Dec. 2001 JSSC Third Harmonic 16

Outline for Compressed Sensing § Motivation for Compressive Sampling § Intuition and Key Ideas § Reconstruction § Experimental Results 17

Motivation for Compressive Sampling § (Medical) Body Area Networks v Many wireless sensors linked to Smartphone, nearby IPAD, etc. v Personal mobile units linked to Dr. via internet/cellular network v Dr. feedback for real-time control of detail vs. energy efficiency § Reduce data rates to increase sensor lifetime and energy efficiency 18

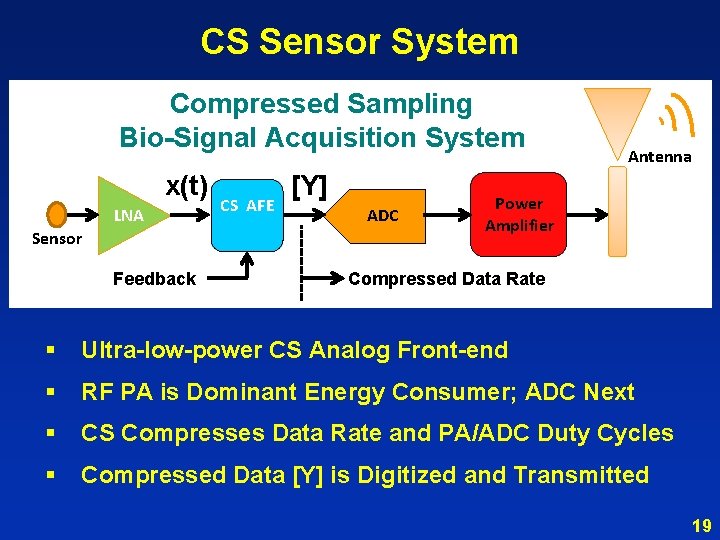
CS Sensor System Compressed Sampling Bio-Signal Acquisition System x(t) Electrode Sensor LNA Feedback CS AFE [Y] ADC Antenna Power Amplifier Compressed Data Rate § Ultra-low-power CS Analog Front-end § RF PA is Dominant Energy Consumer; ADC Next § CS Compresses Data Rate and PA/ADC Duty Cycles § Compressed Data [Y] is Digitized and Transmitted 19

Conventional Sampling § 12 Ball Problem: 11 Light Balls (1 g); 1 Heavy Ball (100 g) § Goal: Identify Heavy Ball in Fewest Measurements § Conventional Sampling requires 12 measurements 20

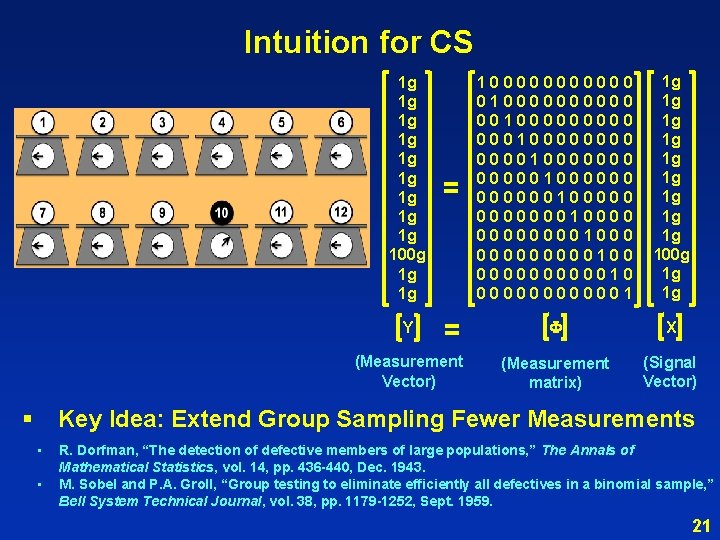
Intuition for CS 1 g 1 g 1 g 100 g 1 g 1 g Y = 1000000 0100000 00100000 0001000010000000100000010000000100001000 00000100 0000010 0000001 1 g 1 g 1 g 100 g 1 g 1 g = F X (Measurement matrix) (Signal Vector) (Measurement Vector) § Key Idea: Extend Group Sampling Fewer Measurements • • R. Dorfman, “The detection of defective members of large populations, ” The Annals of Mathematical Statistics, vol. 14, pp. 436 -440, Dec. 1943. M. Sobel and P. A. Groll, “Group testing to eliminate efficiently all defectives in a binomial sample, ” Bell System Technical Journal, vol. 38, pp. 1179 -1252, Sept. 1959. 21

Random Sampling – 1 102 g = 000000010110 1 g 1 g 1 g 100 g 1 g 1 g § Random Sample to Find Y 11 § Use 1 -b Random Numbers (e. g. , Bernoulli, Toeplitz, Circulant, etc. ) Incoherent Between Rows 22

Random Sampling – 2 102 g 5 g = 000000010110 100011100010 1 g 1 g 1 g 100 g 1 g 1 g § Random Sample to Find Y 21 § Use 1 -b Random Numbers (e. g. , Bernoulli, Toeplitz, Circulant, etc. ) Incoherent Between Rows 23

Random Sampling – 3 102 g 5 g 105 g = 000000010110 100011100010 101100001101 § Random Sample to Find Y 31 § Reconstruction: Two Heavy Measurements—Only #10 Common § Fewer Measurements (e. g. , 3) § CS Works for Sparse Signals 1 g 1 g 1 g 100 g 1 g 1 g § Other (unlikely) Possibilities: § Solution in 1 Measurement § No Solution in M Measurements 24

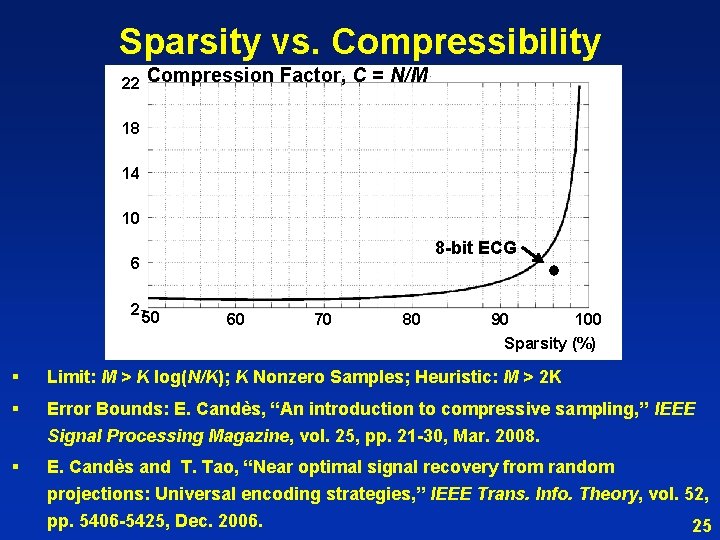
Sparsity vs. Compressibility 22 Compression Factor, C = N/M 18 14 10 8 -bit ECG 6 2 50 60 70 80 90 100 Sparsity (%) § Limit: M > K log(N/K); K Nonzero Samples; Heuristic: M > 2 K § Error Bounds: E. Candès, “An introduction to compressive sampling, ” IEEE Signal Processing Magazine, vol. 25, pp. 21 -30, Mar. 2008. § E. Candès and T. Tao, “Near optimal signal recovery from random projections: Universal encoding strategies, ” IEEE Trans. Info. Theory, vol. 52, pp. 5406 -5425, Dec. 2006. 25

Compressed Sampling - I … [F]MXN = [F 11, …, F 1 N ] ] [ [FM 1, …, FMN ] [Y]MX 1 = [Y 11, …, YM 1] [Y] = [Φ][X] [X]NX 1 = [X 11, …, XN 1] K=3 § [X]16 X 1; [F]8 X 16; [Y]8 X 1; C = 2 § [F] is Gaussian, Uniform, Bernoulli, Toeplitz, etc. § Multiply and sum for each Yij is a Random Linear Projection § [Y] is compressed analog signal with global information § K < M < N for sparse signal such as ECG, EMG, etc. 26

Compressed Sampling - II [X] [Y] § [X]1024 X 1: Analog ECG samples § [Y]256 X 1: Compressed analog output § [F]256 X 1024: Measurement Matrix § C = 4 X 27

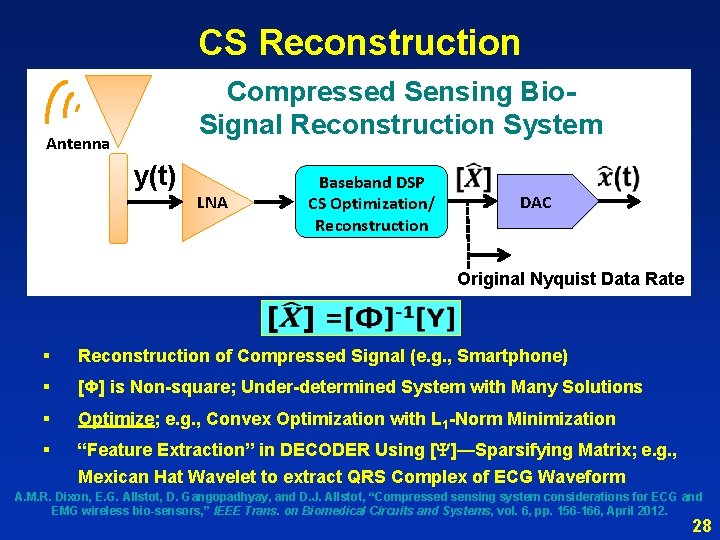
CS Reconstruction Compressed Sensing Bio. Signal Reconstruction System Antenna y(t) LNA Baseband DSP CS Optimization/ Reconstruction DAC Original Nyquist Data Rate § Reconstruction of Compressed Signal (e. g. , Smartphone) § [Φ] is Non-square; Under-determined System with Many Solutions § Optimize; e. g. , Convex Optimization with L 1 -Norm Minimization § “Feature Extraction” in DECODER Using [Y]—Sparsifying Matrix; e. g. , Mexican Hat Wavelet to extract QRS Complex of ECG Waveform A. M. R. Dixon, E. G. Allstot, D. Gangopadhyay, and D. J. Allstot, “Compressed sensing system considerations for ECG and EMG wireless bio-sensors, ” IEEE Trans. on Biomedical Circuits and Systems, vol. 6, pp. 156 -166, April 2012. 28

CS Reconstruction - II [X] [Y] § Accuracy depends on: v Compression Factor, C = N/M v PDF of random coefficients and # bits v Algorithm—Convex Optimization with L 1 Norm 29

Switched-capacitor CS CODER § Electr ode Structure Matrix operations so that input is pipelined. CSADC Eliminates many explicit S/H circuits CSAD C 30

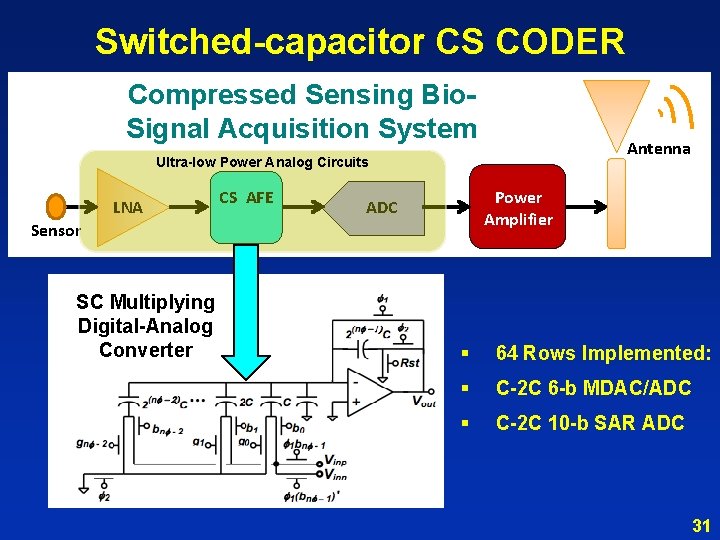
Switched-capacitor CS CODER Compressed Sensing Bio. Signal Acquisition System Ultra-low Power Analog Circuits Electrode Sensor LNA SC Multiplying Digital-Analog Converter CS AFE ADC Antenna [Y]Power = [Φ][X] Amplifier § 64 Rows Implemented: § C-2 C 6 -b MDAC/ADC § C-2 C 10 -b SAR ADC 31

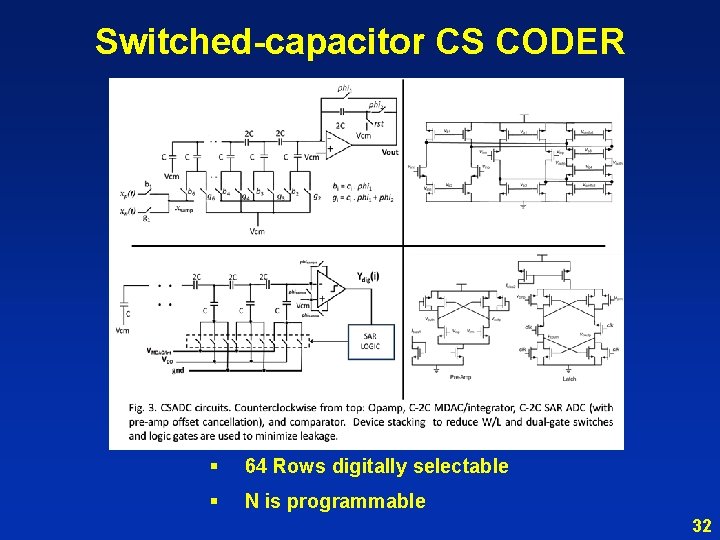
Switched-capacitor CS CODER § 64 Rows digitally selectable § N is programmable 32

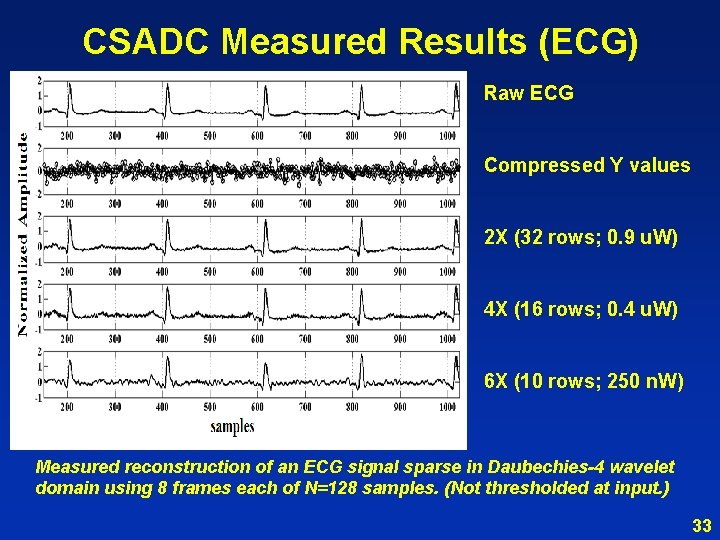
CSADC Measured Results (ECG) Raw ECG Compressed Y values 2 X (32 rows; 0. 9 u. W) 4 X (16 rows; 0. 4 u. W) 6 X (10 rows; 250 n. W) Measured reconstruction of an ECG signal sparse in Daubechies-4 wavelet domain using 8 frames each of N=128 samples. (Not thresholded at input. ) 33

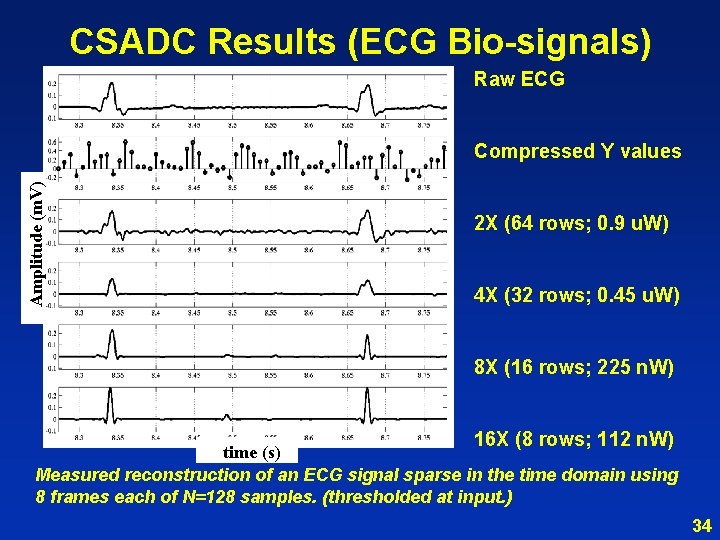
CSADC Results (ECG Bio-signals) Raw ECG Amplitude (m. V) Compressed Y values 2 X (64 rows; 0. 9 u. W) 4 X (32 rows; 0. 45 u. W) 8 X (16 rows; 225 n. W) 16 X (8 rows; 112 n. W) time (s) Measured reconstruction of an ECG signal sparse in the time domain using 8 frames each of N=128 samples. (thresholded at input. ) 34

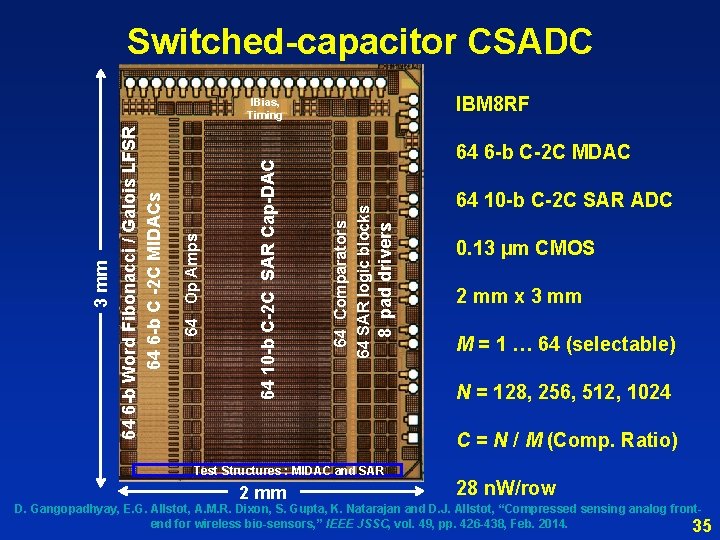
Switched-capacitor CSADC IBM 8 RF 64 6 -b C-2 C MDAC 64 10 -b C-2 C SAR ADC 8 pad drivers 64 Comparators 64 SAR logic blocks 64 10 -b C-2 C SAR Cap-DAC 64 Op Amps 64 6 -b Word Fibonacci / Galois LFSR 64 6 -b C -2 C MIDACs 3 mm IBias, Timing 0. 13 µm CMOS 2 mm x 3 mm M = 1 … 64 (selectable) N = 128, 256, 512, 1024 C = N / M (Comp. Ratio) Test Structures : MIDAC and SAR 2 mm 28 n. W/row D. Gangopadhyay, E. G. Allstot, A. M. R. Dixon, S. Gupta, K. Natarajan and D. J. Allstot, “Compressed sensing analog frontend for wireless bio-sensors, ” IEEE JSSC, vol. 49, pp. 426 -438, Feb. 2014. 35

Future Research Topics N-Path Filters: Blockertolerant front ends Switched Capacitor: High-efficiency, high-power transmitters; Converters Time-to-Digital Converters; Converter: Ring-oscillator amplifiers; Analog-to-Digital Analog-to-digital Converters converters Open Area of Research for Wireless and Biomedical! *Courtesy of Prof. James Buckwalter, UC Santa Barbara 36

Mulţumesc 37