CMOS OpAmp Power Optimization in All Regions of

CMOS Op-Amp Power Optimization in All Regions of Inversion Using Geometric Programming Pablo Aguirre and Fernando Silveira IIE – FING Universidad de la República Montevideo, Uruguay. paguirre@fing. edu. uy

Outline Introduction Geometric Programming (GP) and the gm/ID ratio Relaxed GP Proof of concept: The intrinsic Amplifier Design Example: The Miller Amplifier Conclusions SBCCI 2008 Pablo Aguirre - Fernando Silveira 2

Introduction Automatic analog circuit synthesis: since 1980's Broad classification of techniques: Simulation-based or Equation-based. Optimization methods: we want to assure a global optimum. Three main methods: Branch and bound (B&B), Simulated annealing (SA) and Convex optimization B&B and SA: slow, computational effort grows exponentially with problem size. SA does not guarantee global optimum in practice. Convex optimization: SBCCI 2008 Pros: extremely efficient, can cope with 100’s of vars. and 1000’s of constraints in seconds. Cons: Eqs. must be formulated in posynomial form. Pablo Aguirre - Fernando Silveira 3

GP and the gm/ID ratio GP Problem: Monomials: Posynomials: x: vector real positive vars c, ck: ≥ 0; aik real SBCCI 2008 GP problems can be cast into convex form. Therefore, convex optimization methods guarantee a global solution or will unambiguosly detect that the GP problem is unfeasible. Pablo Aguirre - Fernando Silveira 4

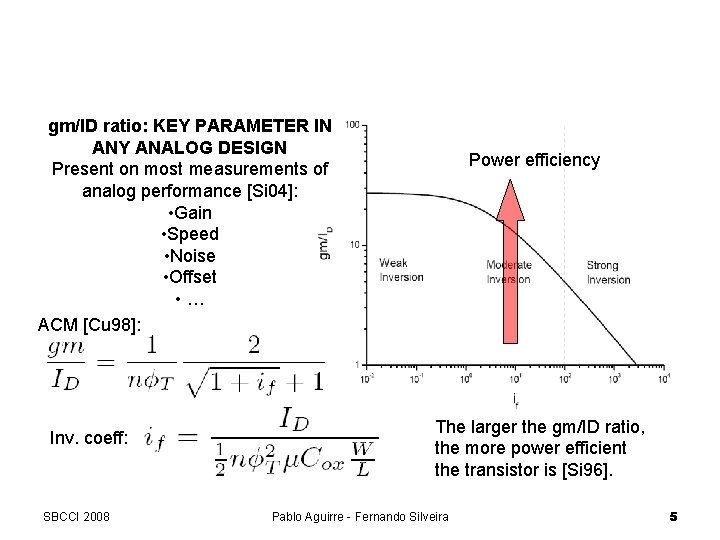
GP and the gm/ID ratio: KEY PARAMETER IN ANY ANALOG DESIGN Present on most measurements of analog performance [Si 04]: • Gain • Speed • Noise • Offset • … ACM [Cu 98]: Inv. coeff: SBCCI 2008 Power efficiency The larger the gm/ID ratio, the more power efficient the transistor is [Si 96]. Pablo Aguirre - Fernando Silveira 5

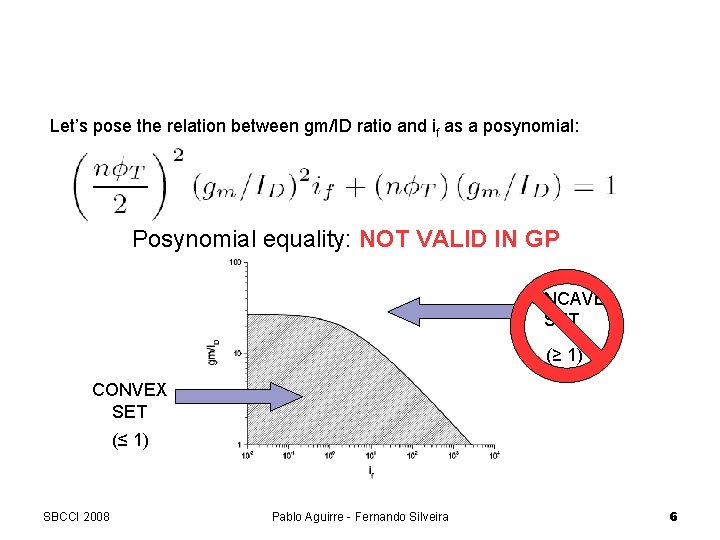
GP and the gm/ID ratio Let’s pose the relation between gm/ID ratio and if as a posynomial: Posynomial equality: NOT VALID IN GP CONCAVE SET (≥ 1) CONVEX SET (≤ 1) SBCCI 2008 Pablo Aguirre - Fernando Silveira 6

Where are we? Where are we heading? Prior ART: Hershenson et al. [He 01] and Mandal et al. [Ma 01]: First report on GP applied to analog CMOS design. STRONG INVERSION ONLY MODELS, therefore not true global optimum. Brodersen et al. [Va 04]: GP on all regions. Uses branch and bound algorithm on top of GP. Looses the computational efficiency of GP. This work: We look for an efficient solution to the posynomial equality of the gm/ID ratio in the case of POWER OPTIMIZATION. This problem is intrinsic to the physics of the MOS transistor. Does not depends on the model used.

Relaxed GP: Original Problem: posynomials monomials Not valid Valid if hi(xs)=1 for all i, then xs is also an optimum for the original GP SBCCI 2008 Pablo Aguirre - Fernando Silveira Global optimum: xs 8

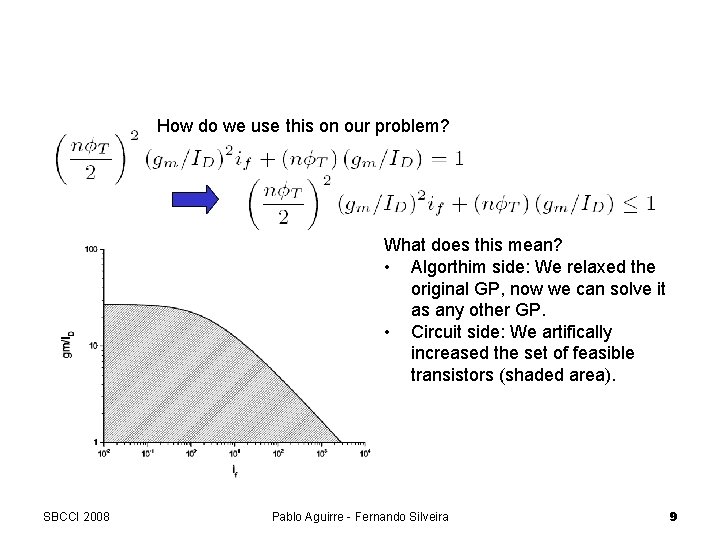
Relaxed GP How do we use this on our problem? What does this mean? • Algorthim side: We relaxed the original GP, now we can solve it as any other GP. • Circuit side: We artifically increased the set of feasible transistors (shaded area). SBCCI 2008 Pablo Aguirre - Fernando Silveira 9

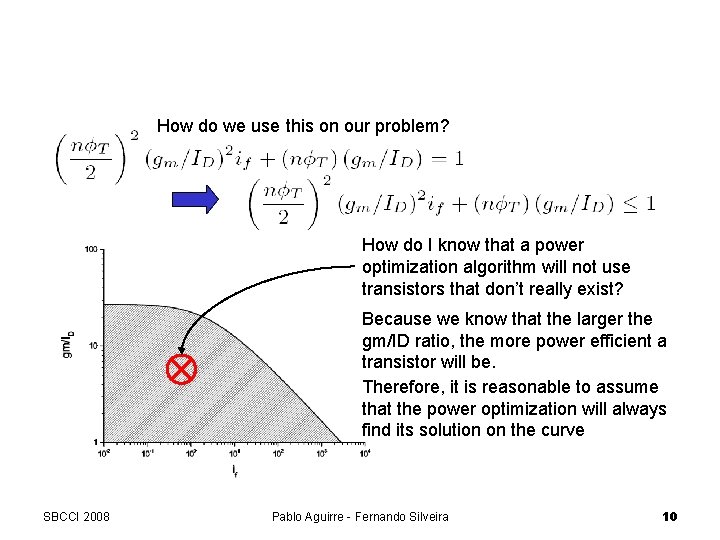
Relaxed GP How do we use this on our problem? How do I know that a power optimization algorithm will not use transistors that don’t really exist? Because we know that the larger the gm/ID ratio, the more power efficient a transistor will be. Therefore, it is reasonable to assume that the power optimization will always find its solution on the curve SBCCI 2008 Pablo Aguirre - Fernando Silveira 10

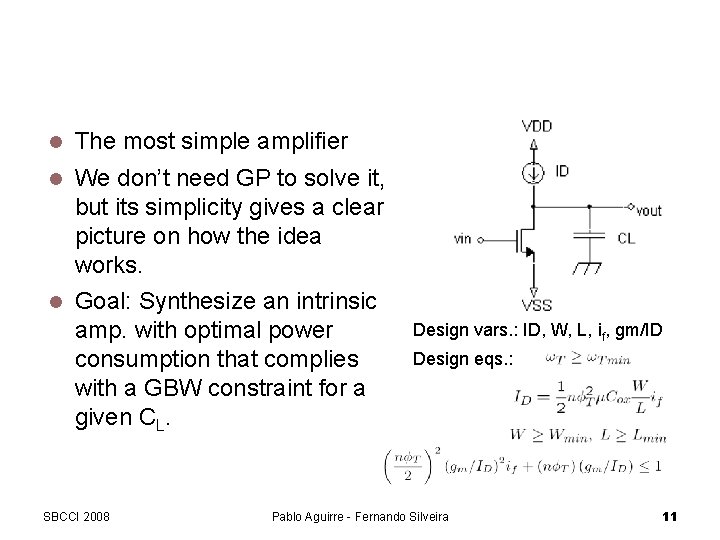
Proof of Concept: The Intrinsic Amplifier The most simple amplifier We don’t need GP to solve it, but its simplicity gives a clear picture on how the idea works. Goal: Synthesize an intrinsic amp. with optimal power consumption that complies with a GBW constraint for a given CL. SBCCI 2008 Design vars. : ID, W, L, if, gm/ID Design eqs. : Pablo Aguirre - Fernando Silveira 11

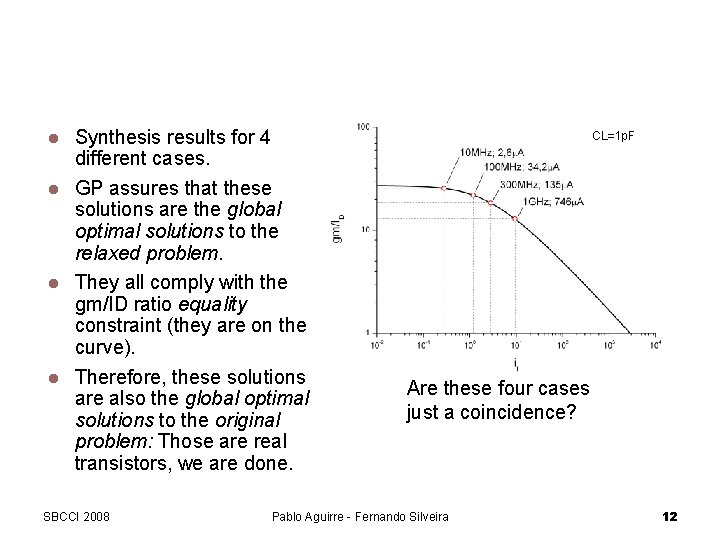
Proof of Concept: The Intrinsic Amplifier Synthesis results for 4 different cases. GP assures that these solutions are the global optimal solutions to the relaxed problem. They all comply with the gm/ID ratio equality constraint (they are on the curve). Therefore, these solutions are also the global optimal solutions to the original problem: Those are real transistors, we are done. CL=1 p. F SBCCI 2008 Are these four cases just a coincidence? Pablo Aguirre - Fernando Silveira 12

The Intrinsic Amplifier: Method Scope Are these four cases just a coincidence? Which is the scope of this approach? Power consumption dictated by gm requirements. Out of scope example: No, formal proof on the paper. Consumption imposed by Slew-rate In these cases: The exception is easily noticed. Increasing the computational effort and complexity around the initial non-valid solution, we can find a valid global optimum. Ex. : Branch and bound [Va 04], Tightening [Bo 05].

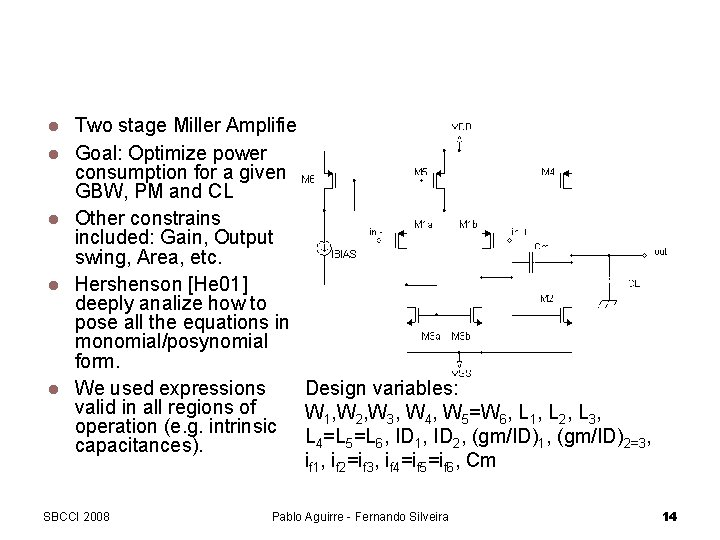
Design Example: The Miller Amplifier Two stage Miller Amplifier Goal: Optimize power consumption for a given GBW, PM and CL Other constrains included: Gain, Output swing, Area, etc. Hershenson [He 01] deeply analize how to pose all the equations in monomial/posynomial form. We used expressions Design variables: valid in all regions of W 1, W 2, W 3, W 4, W 5=W 6, L 1, L 2, L 3, operation (e. g. intrinsic L =L =L , ID , (gm/ID) , 4 5 6 1 2=3 capacitances). if 1, if 2=if 3, if 4=if 5=if 6, Cm SBCCI 2008 Pablo Aguirre - Fernando Silveira 14

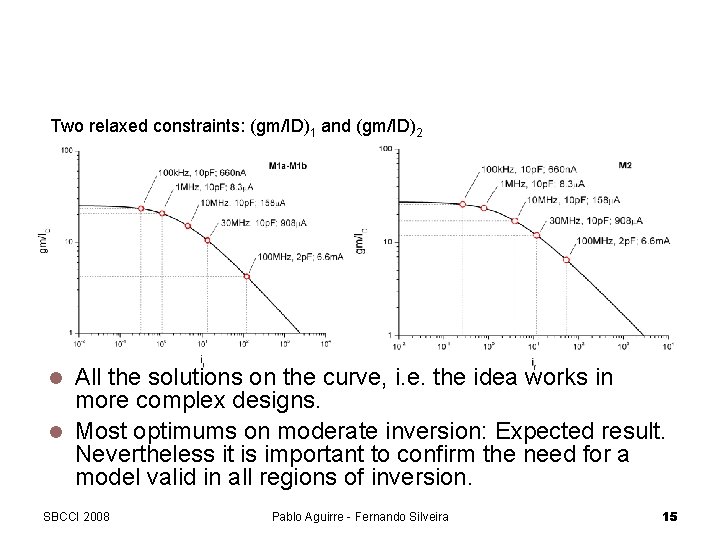
Design Example: The Miller Amplifier Two relaxed constraints: (gm/ID)1 and (gm/ID)2 All the solutions on the curve, i. e. the idea works in more complex designs. Most optimums on moderate inversion: Expected result. Nevertheless it is important to confirm the need for a model valid in all regions of inversion. SBCCI 2008 Pablo Aguirre - Fernando Silveira 15

Conclusions GP applied in CMOS power optimization with true (all regions) global optimum. Posynomial characteristic of the gm/ID curve efficiently handled. This work confirms that power optimums usually lie on moderate inversion region. Future work: Work on the exceptions to handle them efficiently. Inclusion of short channel effects (this work: long channel models only). SBCCI 2008 Pablo Aguirre - Fernando Silveira 16

Acknowledgments PDT - Programa de Desarrollo Tecnológico - Uruguay SBCCI 2008 Pablo Aguirre - Fernando Silveira 17

References [He 01] M. Hershenson, S. Boyd, and T. Lee, “Optimal design of a cmos op-amp via geometric programming, " IEEE Trans. Comput. -Aided Design Integr. Circuits Syst. , vol. 20, no. 1, pp. 121, Jan. 2001. [Ma 01] P. Mandal and V. Visvanathan, “Cmos op-amp sizing using a geometric programming formulation, " IEEE Trans. Comput. -Aided Design Integr. Circuits Syst. , vol. 20, no. 1, pp. 2238, Jan. 2001. [Va 04] J. Vanderhaegen and R. Brodersen, “Automated design of operational transconductance ampliers using reversed geometric programming, " in Proceedings on 41 st Design Automation Conference, vol. I, Jun. 2004, pp. 133 -138. [Si 96] F. Silveira, D. Flandre, and P. G. Jespers, “A (gm/ID) based methodology for the design of cmos analog ircuits and its application to the synthesis of a silicon-on-insulator micropower OTA, " IEEE J. Solid-State Circuits, vol. 31, no. 9, pp. 1314 -1319, Sep. 1996. [Cu 98] A. Cunha, M. Schneider, and C. Galup-Montoro, “An MOS transisotr model for analog circuit design, " IEEE J. Solid-State Circuits, vol. 33, no. 10, pp. 1510 -1519, Oct. 1998. [Bo 05] S. Boyd, S. J. Kim, L. Vandenberghe, and A. Hassibi, “A tutorial on geometric programming, " Stanford University and University of California Los Angeles, Tech. Rep. , 2005. [Online]. Available: http: //www. stanford. edu/~boyd/gptutorial. html [Si 04] F. Silveira and D. Flandre, Low Power Analog CMOS for Cardiac Pacemakers Design and Optimization in Bulk and SOI Technologies, ser. The Kluwer International Series In Engineering And Computer Science. Boston: Kluwer Academic Publishers, Jan. 2004, vol. 758, ISBN 1 -4020 -7719 -X.

CMOS Op-Amp Power Optimization in All Regions of Inversion Using Geometric Programming Pablo Aguirre and Fernando Silveira IIE – FING Universidad de la República Montevideo, Uruguay. paguirre@fing. edu. uy