Cmlap mg mindig termodinamika Carnot s gpek az

Címlap (még mindig) termodinamika Carnot és gépek az axiómák alapján + statisztikus termodinamika Keszei Ernő ELTE Fizikai Kémiai Tanszék http: //keszei. chem. elte. hu/entropia

Miről lesz szó? • ismétlés: a termodinamika axiómái • hogyan lehet alkalmazni őket • hogyan működnek a hőerőgépek, hűtőgépek • statisztikus termodinamika (molekulák világa) • entrópiaszámítások statisztikus módszerrel • az entrópia és a „rendezetlenség” • összefoglalás

A termodinamika alapjai: az axiómák Az axiómákat olyan anyagi testekre mondjuk ki, amelyek homogének és izotrópok, valamint környezetükkel kizárólag (térfogatváltozással járó) mechanikai, termikus, és kémiai kölcsönhatásokban vehetnek részt. („egyszerű rendszerek”) Első axióma 1. Létezik egyensúlyi állapot 2. Az egyensúlyi állapot egyértelműen meghatározott 3. Az egyensúlyi állapot K + 2 szabadsági fokú (egyszerű rendszerekben!) 2. Az egyensúlyi állapot nem függhet a rendszer „előéletétől” 3. Az U, V és n 1, n 2, … n. K állapotváltozók rögzítik az állapotot; ezek f(U, V, n 1, n 2, … n. K) függvényei állapotfüggvények.

A termodinamika alapjai: az axiómák Definíció: összetett rendszer: legalább két részből áll a két alrendszert egy fal (kényszerfeltétel) választja el Második axióma 1. Az entrópia csak egyensúlyi állapotra van értelmezve 2. Az izolált összetett rendszer egyensúlya abban az állapotban valósul meg, ahol az entrópia maximális. Harmadik axióma 1. Az S (U, V, n 1, n 2, … n. K ) extenzív függvény, és matematikai szempontból „jól viselkedik”; az energiára nézve invertálható: az U (S, V, n 1, n 2, … n. K ) az entrópiafüggvény belőle kiszámítható. 2. Ha az entrópiafüggvényt ismerjük, minden egyensúlyi állapotot meg tudunk határozni belőle: az S = S (U, V, n 1, n 2, … n. K ) fundamentális egyenlet. Ezzel egyenértékű az U = U (S, V, n 1, n 2, … n. K ) egyenlet is; azaz fundamentális egyenlet.

A termodinamika alapjai: az axiómák Negyedik axióma Ahol a értéke zérus, azaz zérus hőmérsékleten az entrópia pontosan zérus. (abszolút zérus, azaz 273, 16 °C) Az entrópia skálája – az energiaskálával ellentétben – jól meghatározott. (Ezért tudunk pl. kémiai egyensúlyi állandót számítani. ) („Maradék entrópia”: nincs egyensúly!!)

Összefoglalva az axiómákat: Az (egyszerű) termodinamikai rendszerek leírhatók K + 2 extenzív változóval. Ezek extenzív függvényei változóikban homogén lineárisak. E függvények deriváltjai változóikban homogén nulladrendűek. A termodinamikai feladatok többváltozós függvények differenciál- és integrálszámításaira vezethetők vissza. Az egyensúlyok számítása a fundamentális egyenletek ismeretében szélsőérték-feladatokra vezethető vissza. Az axiómák és a fundamentális egyenletek ismeretében minden termodinamikai feladat megoldható.

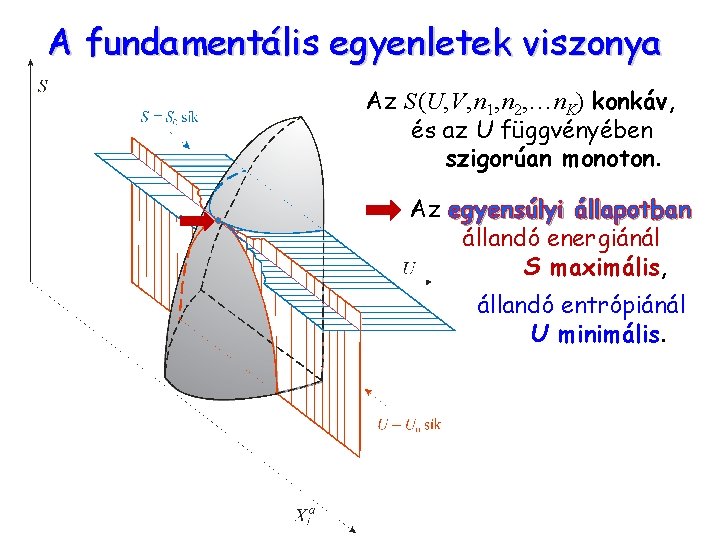
A fundamentális egyenletek viszonya Az S (U, V, n 1, n 2, … n. K) konkáv, és az U függvényében szigorúan monoton. Az egyensúlyi állapotban állandó energiánál S maximális, állandó entrópiánál U minimális.

A fundamentális egyenletek viszonya Egyensúly állandó energiánál (izolált rendszerben): az S (U, V, n 1, n 2, … n. K) függvény maximuma. Egyensúly állandó entrópiánál (izentropikus rendszerben): az U (S, V, n 1, n 2, … n. K) függvény minimuma. (Egyszerű rendszerben izentropikus = adiabatikus) A szélsőérték-feladatok megoldásához az elsőrendű differenciálok zérus értékét keressük:

A deriváltak azonosítása Tudjuk: állandó S és n mellett (zárt, adiabatikus rendszerben) (Ez a térfogati munka. ) Hasonlóan: állandó V és n mellett (zárt, merev falú rendszerben) (Ez a rendszerrel közölt hő. ) A derivált tulajdonságai később igazolják: Állandó S és V mellett (merev, adiabatikus rendszerben) (Ez az energiaváltozás anyagtranszport hatására. ) Ezt a deriváltat nevezzük el kémiai potenciálnak:

A deriváltak azonosítása a nyomás, a hőmérséklet, pedig a kémiai potenciál. Ezek felhasználásával a teljes differenciál átírható az egyszerűbb alakba.

Fundamentális egyenletek és állapotegyenletek Energia-alapú fundamentális egyenlet: U = U(S, V, n) Differenciális alakja: Állapotegyenletek: Entrópia-alapú fundamentális egyenlet: S = S(U, V, n) Differenciális alakja: Állapotegyenletek:

Egyensúlyi feltételek Intenzív változókkal: az adott kölcsönhatásra jellemző változók azonossága: Termikus egyensúly: T φ T , Mechanikai egyensúly: P φ P , Kémiai egyensúly: μ φ μi , i Kémiai egyensúly esetén komponensenként külön feltétel írható fel; minden olyan komponensre, amely szabadon átjárhat az összetett rendszer alrendszerei között. Egyszerűen kiterjeszthető más kölcsönhatásra jellemző változókra is: Pl. elektromos egyensúly: Ψ φ Ψ ,

Egyensúlyi feltételek Extenzív változókkal: a megfelelő potenciálfüggvények extrémuma: körülmények az egyensúly feltétele U és V állandó S (U, V, n) maximuma S és V állandó U (S, V, n) minimuma S és P állandó H (S, P, n) minimuma T és V állandó F (T, V, n) minimuma T és P állandó G (T, P, n) minimuma feltételi egyenlet stabilitási feltétel Szükség esetén további (entrópiajellegű) potenciálfüggvények is alkalmazhatók.

Néhány szó a tankönyvről 1. Bevezetés 2. A termodinamika axiómái 3. Termodinamikai egyensúly izolált és állandó entrópiájú rendszerekben 4. Termodinamikai egyensúly egyéb feltételek esetén 5. Termodinamikai folyamatok és gépek 9– 80 oldal 6. Elegyek (többkomponensű rendszerek) termodinamikai leírása 7. Fázisegyensúlyok 8. Kémiai reakciók egyensúlya 9. A termodinamikai leírás kiterjesztése további kölcsönhatásokra 10. A statisztikus termodinamika alapjai 252– 288 oldal 11. Egyensúly előtt – a traszportfolyamatok elemei Függelék

Néhány szó a tankönyvről Függelék F 1. Többváltozós függvényekre vonatkozó néhány összefüggés F 2. Extenzív változók cseréje intenzív változókra: A Legendre-transzformáció F 3. A klasszikus termodinamika főtételei

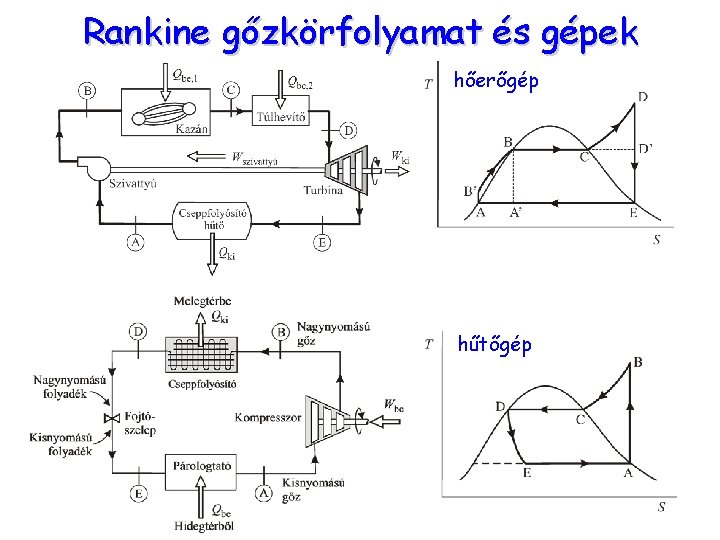
Rankine gőzkörfolyamat és gépek hőerőgép hűtőgép

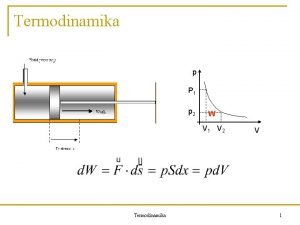
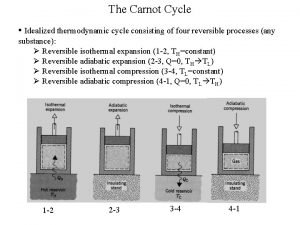
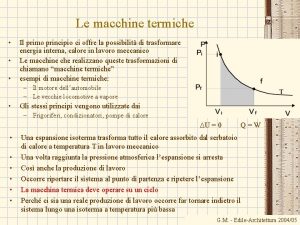
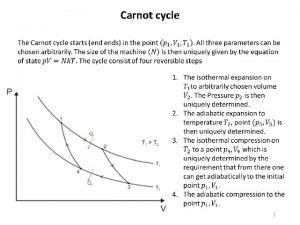
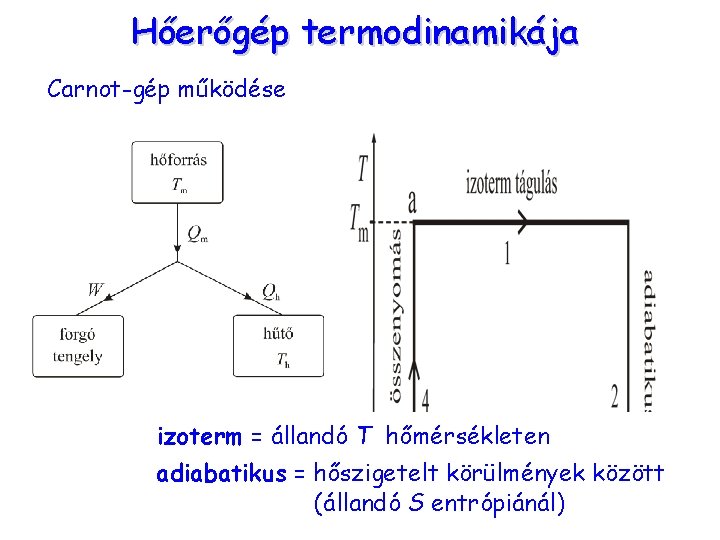
Hőerőgép termodinamikája Carnot-gép működése izoterm = állandó T hőmérsékleten adiabatikus = hőszigetelt körülmények között (állandó S entrópiánál)

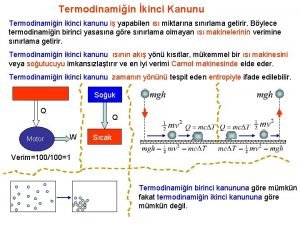
Hőerőgép termodinamikája Carnot körfolyamat Körfolyamat: visszatér a kiindulási állapotba a végén S is, U is ugyanaz, mint az elején: ΔS = 0 és ΔU =0 ΔU = Wbe - Wki + Q be - Q ki = 0 Wki - Wbe = Q be - Q ki A Carnot körfolyamat Q = T ΔS η hatásfoka:

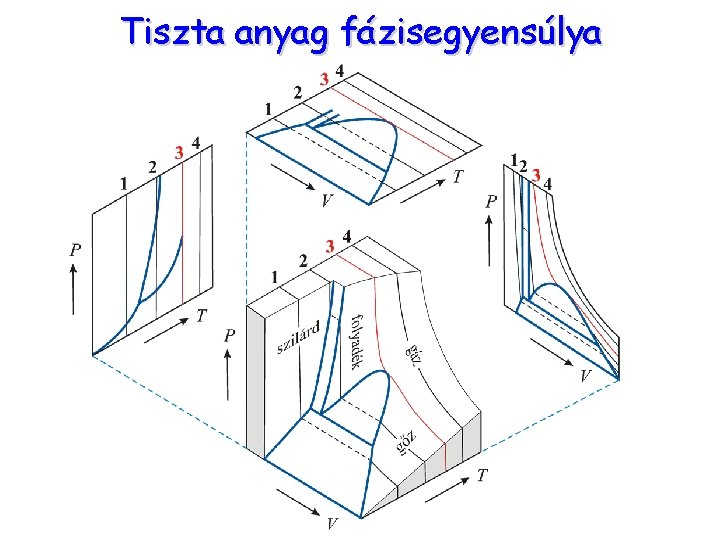
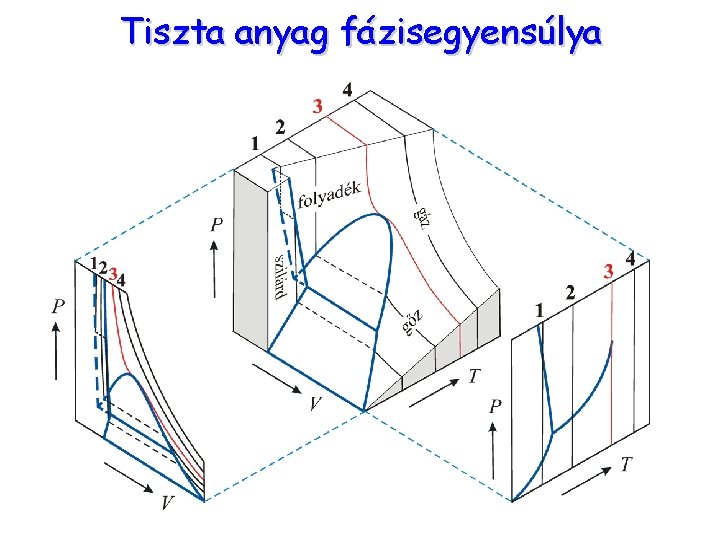
Tiszta anyag fázisegyensúlya

Tiszta anyag fázisegyensúlya

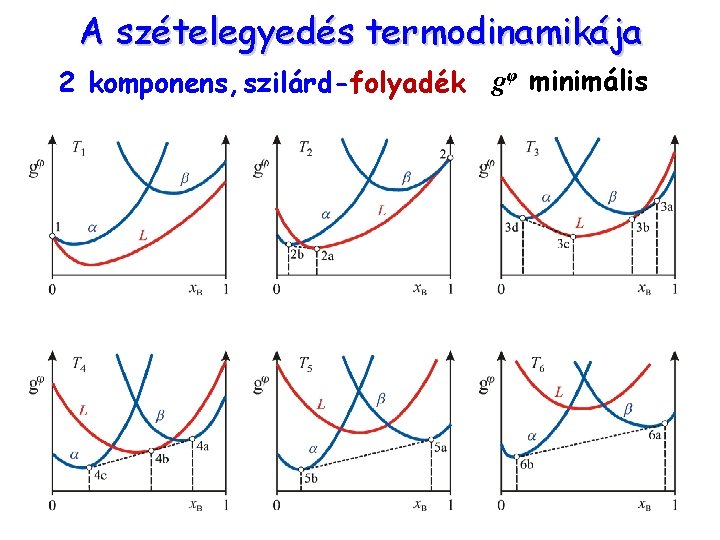
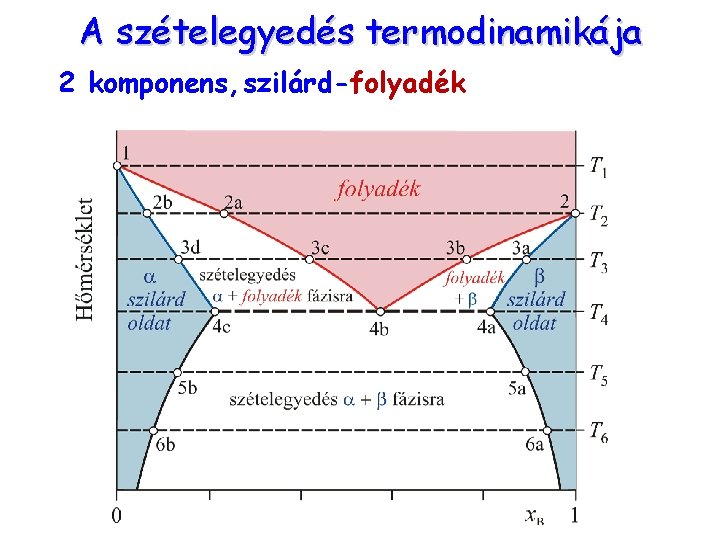
A szételegyedés termodinamikája 2 komponens, szilárd-folyadék gφ minimális

A szételegyedés termodinamikája 2 komponens, szilárd-folyadék

Bevezetés 1 (innen) Statisztikus termodinamika A termodinamikában használt alapmennyiségek (U, S, V, ni , T, P, stb. . . ) között csak egy van, amelyet újként kellett a megtanulni: az entrópia. (A többi új mennyiség ebből már származtatható. ) A termodinamikából azt is tudjuk, hogy ha ismerjük egy adott rendszer fundamentális egyenletét, akkor összes lehetséges állapotát ismerjük. A fundamentális egyenlet alakja lehet pl. S = S (U, V, n ) A STATISZTIKUS TERMODINAMIKA fő célja: a rendszert alkotó részecskék (molekulák) egyszerű fizikai tulajdonságaiból meghatározni a fundamentális egyenletet. Ezzel egyúttal közelebbről meghatározzuk az entrópiát is: Értelmezzük az entrópiát a molekulák sokaságának tulajdonságai alapján.

Bevezetés 2 A STATISZTIKUS TERMODINAMIKAI LEÍRÁST (mint ahogy a klasszikus termodinamikában is tettük) egy EGYSZERŰ, IZOLÁLT rendszerrel kezdjük. EGYSZERŰ rendszer: makroszkopikusan homogén, izotróp, (elektromosan) töltetlen, (kémiailag) inert, (térfogatához képest) kis felületű, elektromos, mágneses és gravitációs tértől mentes. IZOLÁLT rendszer: U, V, és n állandó. Az EGYSZERŰ, IZOLÁLT rendszer legyen EGYKOMPONENSŰ is. Az n mólszám (ez persze a IUPAC kedvéért anyagmennyiség) helyett használjuk a molekulák (részecskék) N számát. Egy ilyen rendszer modelljét nevezzük mikrokanonikus sokaságnak.

MIKROKANONIKUS SOKASÁG 1 Tekintsük az EGYSZERŰ, IZOLÁLT (EGYKOMPONENSŰ) rendszert. Egy ilyen rendszer modelljét nevezzük mikrokanonikus sokaságnak. MIKROKANONIKUS SOKASÁG: N részecske E összenergiával V térfogatban Mit jelent itt a sokaság (populáció) ? Mi is az pontosan? A KVANTUMMECHANIKA szerint nagy részecskeszám (N 1020) esetén a rendszernek igen sok olyan kvantumállapota lehet, amely az előírt N, E, V értékekkel összeegyeztethető – ezek alkotják a sokaságot.

Mikrokanonikus sokaság 2 kis kvantummechanika, ami azért nem fog fájni Most egy (csak két igen egyszerű dolgot kell belőle ismerni): Tegyük fel, hogy a rendszer éppen egy adott kvantumállapotban van. Ez az állapot azonban nem változatlan: a kvantummechanika szerint még egyetlen részecske különböző állapotai között is van véges átmeneti valószínűség. 1020 nagyságrendű részecskeszám esetén a rendszer kvantumállapotai nagyon sűrűn helyezkednek el, és az állapotok között igen nagy valószínűséggel, gyorsan történnek átmenetek. Ezeket az átmeneteket véletlen folyamatok váltják ki, ezért várható, hogy a részecskerendszer bármely állapotból bármely másikba átmehet. Ezt fejezi ki a statisztikus fizika egyetlen alapfeltevése (axiómája): Mikrokanonikus sokaságban az állandó E, V, N feltétellel összeegyeztethető minden egyes kvantumállapot ugyanakkora valószínűséggel fordul elő, ha a sokaság a rendszer egyensúlyát reprezentálja.

Az időtengely megfordíthatatlan A mikrokanonikus sokaság állapotai tehát egyensúlyban egyenletes eloszlásúak az eseményteret alkotó kvantumállapotok fölött. Mit jelent ez? Ha az (E, V, N ) mikrokanonikus sokaságnak megfelelő rendszert egy adott kvantumállapotból indítjuk, egyensúly akkor lehet, ha a rendszer az összes lehetséges állapotot – tehát az elérhető állapotok maximumát – azonos valószínűséggel járja be. Ez egyrészt emlékeztet a termodinamika 2. axiómájára: egyensúly esetén (izolált rendszerben) az entrópia maximális. Ez megnyugtató. Másrészt azonban van egy érdekes következménye: a rendszer véletlenszerűen (egyenletesen) bejárja az összes lehetséges állapotot. Ha a rendszert „időben visszafelé” indítjuk, akkor a mechanika törvényei szerint vissza kellene jutni a kiindulási állapotba (ahonnan először indult). Ezt viszont nem teszi meg, hanem ekkor is véletlenszerűen (egyenletesen) járja be az állapotokat. Hová tűnt az időtengely megfordíthatósága? ? (Ez már kevésbé megnyugtató. ) Válasz: az időtengely megfordíthatósága pontosan a véletlen perturbációk (azaz a kvantummechanika érvényessége) miatt tűnt el: Adott kezdeti állapot „újra-előfordulásának” valószínűsége csak akkora lesz, mint bármely másik állapoté. (Ez már valamivel megnyugtatóbb. )

Mikrokanonikus entrópia 1 Vizsgáljuk meg az analógiát az állapotok maximumának bejárása és az izolált rendszerek entrópiája között. Osszunk ketté gondolatban egy adott (E, V, N ) mikrokanonikus sokaságnak megfelelő termodinamikai rendszert: E 1 , V 1 , N 1 E 2 , V 2 , N 2 (Ez megfelel egy gondolatban két alrendszerre osztott izolált rendszernek. ) Erre felírhatjuk az E = E 1 + E 2 V = V 1 + V 2 N = N 1 + N 2 összefüggéseket. Tudjuk, hogy a két alrendszer fölött az entrópia is additív: S (E, V, N ) = S 1 (E 1 , V 1 , N 1 ) + S 2 (E 2 , V 2 , N 2 )

Mikrokanonikus entrópia 2 Az állapotok számáról viszont azt tudjuk, hogy a teljes rendszerben a két rendszer állapotainak száma összeszorzódik: (E, V, N ) = 1 (E 1 , V 1 , N 1 ) 2 (E 2 , V 2 , N 2 ) Az egyesített rendszerben az S = S 1 + S 2 additivitás is fennáll. A kettő egyszerre csak akkor lehet igaz, ha fennáll az alábbi összefüggés: S ( E, V, N ) = k ln ( E, V, N )

Mikrokanonikus entrópia 3 S ( E, V, N ) = k ln ( E, V, N ) Vegyük észre, hogy ez az entrópia kifejezése a mikrokanonikus rendszer összes lehetséges állapotának számával. Ez akkor lesz összhangban a termodinamikában használt Kelvin-féle hőmérsékleti skálával, ha a k együttható éppen a Boltzmann konstans: k = 1. 3807 · 10– 23 J / K (A konstans mindössze egy skálafaktor, ami az entrópiát skálázza. ) k értékének ilyen megválasztása mellett a termodinamikából jól ismert deriváltra éppen a Kelvin hőmérséklet reciprokát kapjuk.

Boltzmann S ( E, V, N ) = k ln ( E, V, N ) Wien, Zentralfriedhof (Simmering) Johannes Borromäus templom

A MIKROKANONIKUS FORMALIZMUS ÖSSZEFOGLALÁSA A sokaság állapotainak valószínűségi sűrűségfüggvénye: N részecske E összenergiával V térfogatban Az mennyiség neve: állapotösszeg, vagy partíciós függvény. (Zustandssumme) (partition function) A statisztikus termodinamika mikrokanonikus formalizmusa az entrópia-bázisú fundamentális egyenlethez vezet, melynek alakja: S ( E, V, N ) = k ln ( E, V, N ) A mikrokanonikus „recept” tehát nagyon egyszerű: Számoljuk össze a lehetséges állapotokat, és abból egyszerűen kiszámíthatjuk az entrópiafüggvényt. Ezzel egyúttal meghatároztuk a termodinamikai rendszer minden lehetséges makroszkopikus állapotát is.

KANONIKUS SOKASÁG 1 Az izolált rendszer nem igazán érdekes. Nézzünk ezért egy másikat. KANONIKUS SOKASÁG: N részecske V térfogatban T hőmérsékleten A rendszer, amit ez a sokaság modellez, már lehetőséget ad változásokra: N részecske V térfogatban, amely belemerül egy T hőmérsékletű hőtartályba (fala pedig hővezető). (A termodinamikából egyébként tudjuk, hogy ez az egyensúly az F szabadenergiával (Helmholtz potenciállal) jellemezhető könnyen. ) Ebben az esetben az energia a sokaságban nincs lerögzítve, így bármely E energia elérhető a sokaság számára. A különböző állapotok azonban ebben a sokaságban nem azonos valószínűségűek.

Kanonikus sokaság 2 Az állapotok feletti eloszlás kiszámításához a rendszert és a hőtartályt egyetlen izolált összetett rendszernek tekintjük. (Így jártunk el a termodinamikában is. ) Tekintsünk egy analógiát! Legyen egy piros és dobókockánk. (A fehér kockák jelentik a tartályt. ) Nézzük először azt, mekkora a valószínűsége a három kocka egy adott „konfigurációjának”. Nyilván minden konfiguráció valószínűsége azonos. (1 / 63 = 1 / 216) Ha csak a piros kockát dobjuk egyedül, ott is azonos minden szám valószínűsége. Így az 1, 2, 3, 4, 5, 6 számok mindegyike 1/6 valószínűséggel fordul elő. Számítsuk ki, mekkora a piros kockán az 1, 2, 3, 4, 5, 6 számok előfordulásának feltételes valószínűsége, ha a három kocka dobásakor csak azokat az eseteket vesszük figyelembe, ahol a dobott számok összege 12. (Az „összenergia” megfelelője az egyesített rendszerben. )

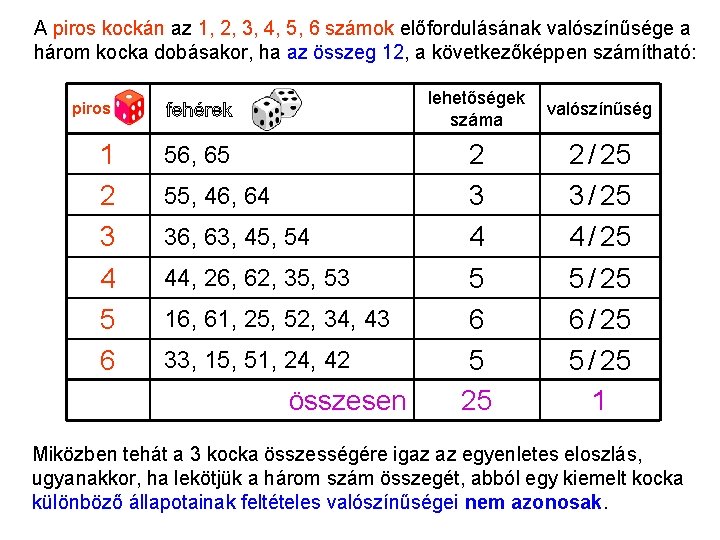
Kanonikus sokaság 3 A piros kockán az 1, 2, 3, 4, 5, 6 számok előfordulásának valószínűsége a három kocka dobásakor, ha az összeg 12, a következőképpen számítható: piros 1 2 3 56, 65 4 5 6 44, 26, 62, 35, 53 55, 46, 64 36, 63, 45, 54 16, 61, 25, 52, 34, 43 33, 15, 51, 24, 42 összesen lehetőségek száma valószínűség 2 3 4 2 / 25 3 / 25 4 / 25 5 6 5 25 5 / 25 6 / 25 5 / 25 1 Miközben tehát a 3 kocka összességére igaz az egyenletes eloszlás, ugyanakkor, ha lekötjük a három szám összegét, abból egy kiemelt kocka különböző állapotainak feltételes valószínűségei nem azonosak.

Kanonikus sokaság 4 Az előbbi analógia alapján levonhatjuk az alábbi következtetést: A termosztált alrendszer adott i állapotának valószínűsége kiszámítható az alrendszer Ei energiájával összeegyeztethető tartály-állapotok számának és a teljes rendszer (tartály + alrendszer) összes állapotai számának hányadosaként: Etot : az összenergia Ei : a termosztált rendszer energiája res (Etot – Ei ) : az elérhető állapotok száma a tartályban, ha a termosztált rendszer energiája Ei tot (Etot) : az egyesített rendszer összes elérhető állapotának száma

Kanonikus sokaság 5 A kifejezésbe írjuk be az állapotok számának helyébe annak entrópiával kifejezett értékét a megfelelő mikrokanonikus összefüggés alapján: Ha S ( E, V, N ) = k ln ( E, V, N ) , akkor ( E, V, N ) a logaritmusfüggvény inverzével adható meg: Ez ugyan már a kanonikus eloszlás sűrűségfüggvénye, de ebben az alakban még nem megfelelő…

……………kissé fáradtságos számolások után: KANONIKUS SOKASÁG: N részecske V térfogatban T hőmérsékleten a sokaság i állapotainak valószínűségi sűrűségfüggvénye a kanonikus állapotösszeg, vagy kanonikus partíciós függvény A statisztikus termodinamika kanonikus formalizmusa a szabadenergia-bázisú fundamentális egyenlethez vezet, melynek alakja: A kanonikus „recept” tehát a következő: számítsuk ki az állapotösszeget, és abból a szabadenergia-függvényt.

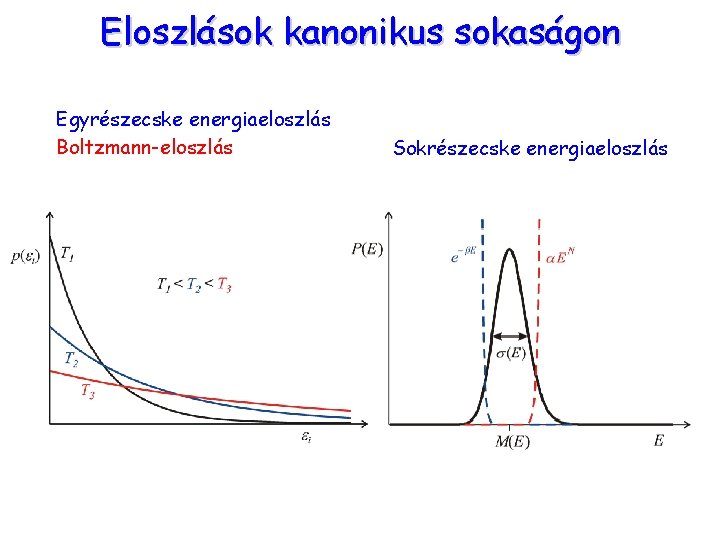
Eloszlások kanonikus sokaságon Egyrészecske energiaeloszlás Boltzmann-eloszlás Sokrészecske energiaeloszlás

Az entrópia mint rendezetlenség 1 Az entrópia általános értelmezéséről Könnyen belátható, hogy az entrópia éppen a sűrűségfüggvény logaritmusának az alakban felírható várható értéke. Mikrokanonikus esetben ugyanis , és ekkor

Az entrópia mint rendezetlenség 3 Milyen értelemben nevezhető „rendezetlenségnek” az 1) Ha a pi sűrűségfüggvényben valamelyik i-hez 1 tartozik (az összes többi zérus), akkor A rendezetlenség S = – k · 1 · ln 1 = 0 mértéke zérus 2) A rendezetlenség maximuma az egyenletes eloszláshoz tartozik – ha a lehetőségek közül egy sincs kitüntetve. (véletlenszerű bejárás). 3) A rendezetlenség maximuma monoton nő, ha az egyenletes eloszlásban a lehetőségek száma ( ) nő. 4) A rendezetlenség additív a részrendszerek felett: Az entrópiára a „rendezetlenség” kifejezést tehát (csak) a fenti értelemben – azaz körültekintően – lehet alkalmazni.

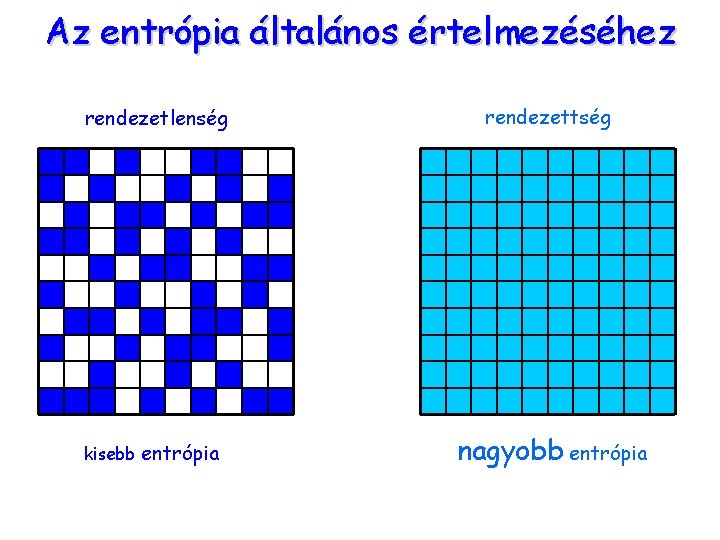
Az entrópia általános értelmezéséhez rendezetlenség rendezettség kisebb entrópia nagyobb entrópia

Összefoglalás • ismétlés: a termodinamika axiómái • axiómák alkalmazása • hőerőgépek működése, hatásfoka • statisztikus termodinamika (molekulák világa) • entrópiaszámítások statisztikus módszerrel • az entrópia és a „rendezetlenség”

Összefoglalás Köszönöm a figyelmüket!