Clustershell Competition in Light Nuclei N Itagaki University

Cluster-shell Competition in Light Nuclei N. Itagaki, University of Tokyo S. Aoyama, Kitami Institute of Technology K. Ikeda, RIKEN S. Okabe, Hokkaido University

Purpose of the present study • Construction of an unified model which can express both shell and cluster structures • To show that the cluster structure becomes more important in neutron-rich nuclei （weakly bound systems）

The first step of the construction of the Unified model is to establish the description of excess nucleons around clusters Molecular-Orbit is a bridge from Cluster model to Unified model α α 8 Be（α-α) - core case We can make a connection from the cluster physics to the physics of Neutron-rich nuclei

The MO approach in nuclear physics “Molecular Viewpoints in Nuclear Structure” J. A. Wheeler, Physical Review 52 (1937) Applied to 9 Be in 1973 Y. Abe, J. Hiura, and H. Tanaka, P. T. P. 49 (application of LCAO-SCF method to nuclear systems) Systematic Analyses of the Be isotopes M. Seya, M. Kohno, and S. Nagata, P. T. P. 65 (1981) π- and σ-orbits are described as linear combination of p-orbits (Gaussian around each α-cluster with zero distance)

Hamiltonian 2 -body effective interaction

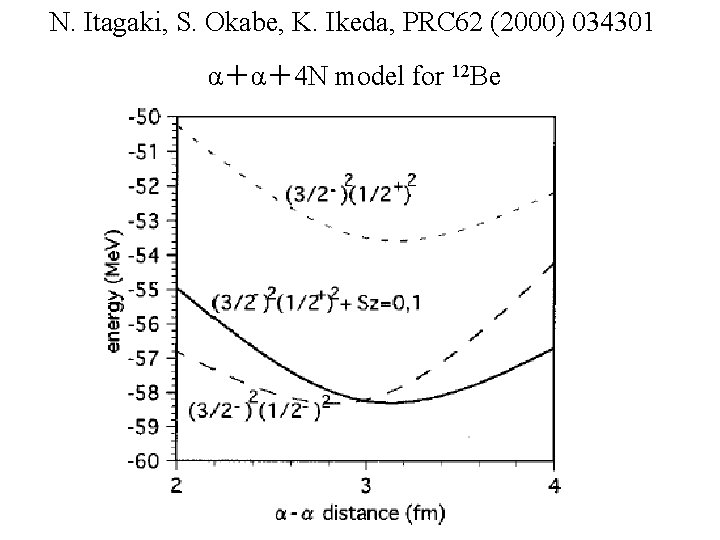
N. Itagaki, S. Okabe, K. Ikeda, PRC 62 (2000) 034301 α＋α＋4 N model for 12 Be

The significance of present analysis on Be isotopes • The application of MO to nuclear systems has been done on a large-scale (the idea itself has existed for a long time). • It is shown once again that cluster physics is closely related to the physics of unstable nuclei （importance of cluster structure in neutron-rich nuclei） • Now the research is extended to more exotic clusters with excess neutrons

Significance of the present analysis on C isotopes • We have re-realized the difference between atomic physics and nuclear physics. In general, it is difficult to stabilize the linearchain configuration of 3α 　 But there is possibilities when excess neutrons rotate around the core • Experiments have been done, and some candidates are already observed.

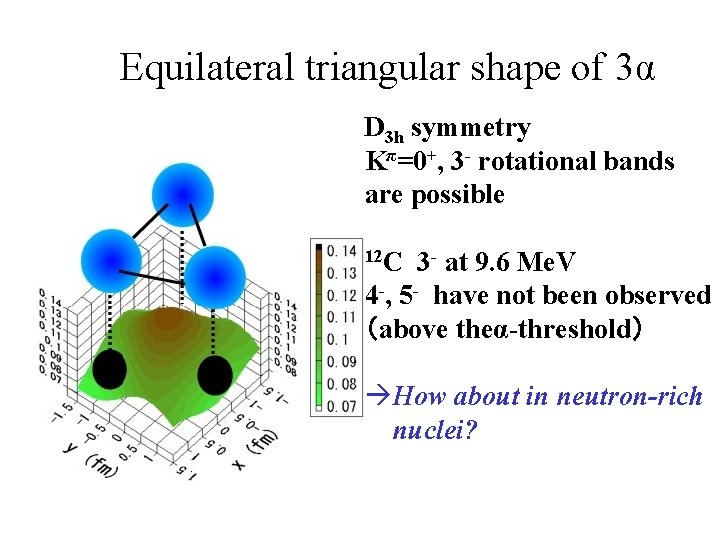
Equilateral triangular shape of 3α D 3 h symmetry Kπ=0+, 3 - rotational bands are possible 12 C 3 - at 9. 6 Me. V 4 -, 5 - have not been observed （above theα-threshold） How about in neutron-rich nuclei?

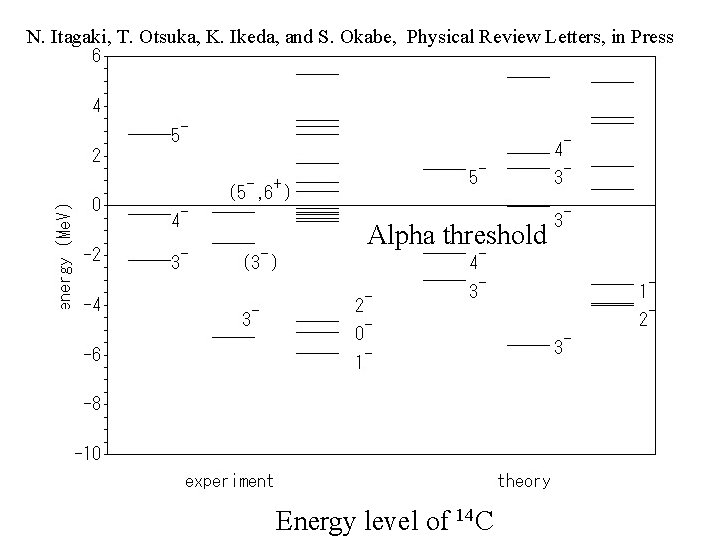
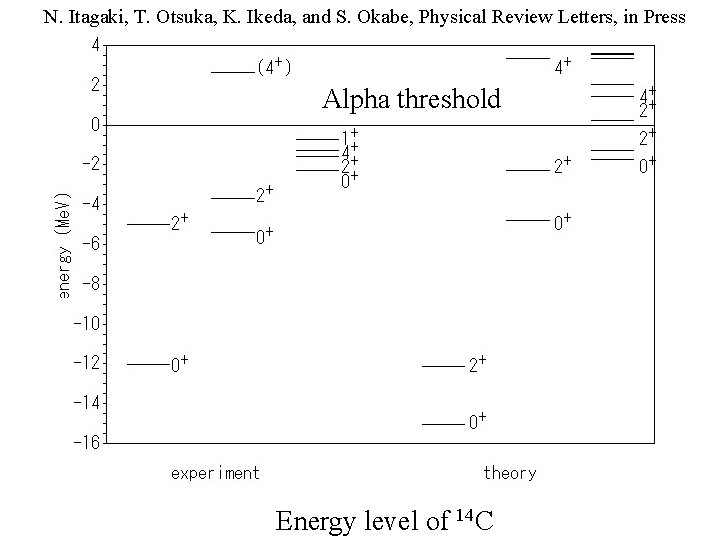
N. Itagaki, T. Otsuka, K. Ikeda, and S. Okabe, Physical Review Letters, in Press Alpha threshold Energy level of 14 C

N. Itagaki, T. Otsuka, K. Ikeda, and S. Okabe, Physical Review Letters, in Press Alpha threshold Energy level of 14 C

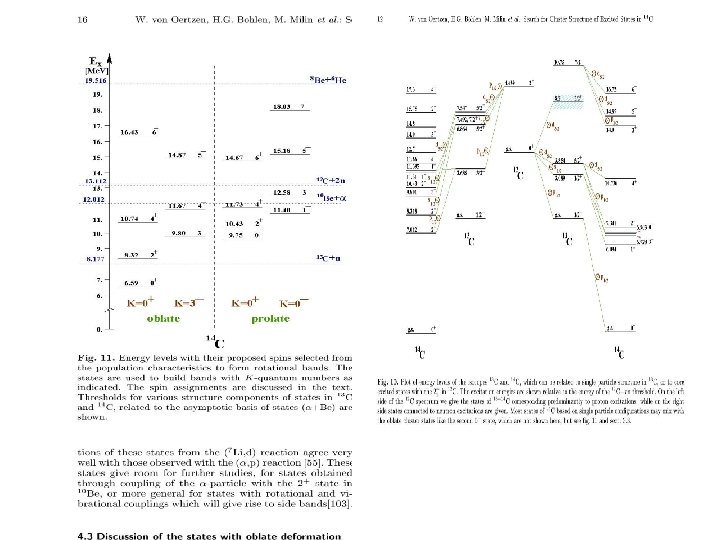
Ikeda’s diagram Cluster structure should appear around the corresponding threshold energy of the cluster emission Threshold rule

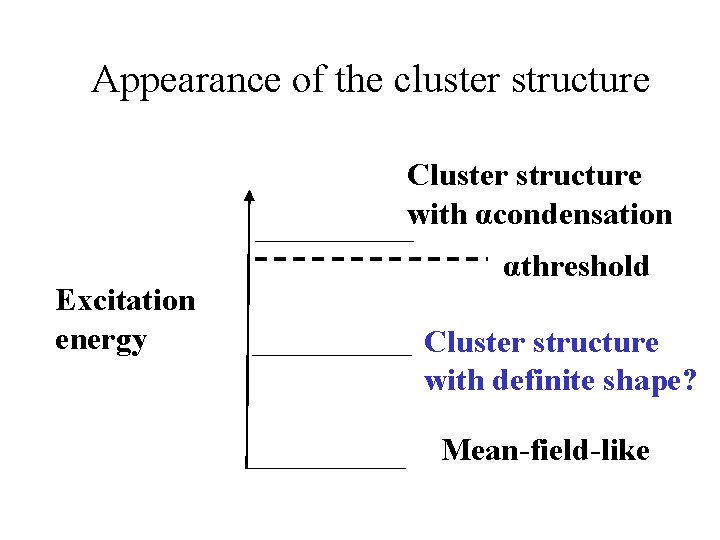
Appearance of the cluster structure Cluster structure with αcondensation Excitation energy αthreshold Cluster structure with definite shape? Mean-field-like

Further extension of the MO approach MO is a good tool to describe the wave nature of valence neutrons around the cluster core But… Number of Slater determinant is huge Ex. 84 = 4096 Even if the core-degree of freedom is fixed

Antisymmetrized Molecular Dynamics (AMD) (H. Horiuchi et al. ) 　Single-particle wave function Slater determinant　　　 　　　　　　 Φ　＝　A [(ψ1χ1)(ψ2χ2)(ψ3χ3)・・・] 　 Projection of parity and angular momentum　　　　　　Ψ　＝　PJ　Pπ　Φ

AMD – Superposition of Selected Snapshots (AMD triple S) • We superpose many AMD wave functions • They are randomly generated, and cooling equation is applied only for the imaginary part (spin-orbit contribution is incorporated) • We use the idea of Stochastic Variation Method （ Suzuki, Varga …）for the selection of the basis N. Itagaki and S. Aoyama, PRC 68 (2003) 054302

AMD cooling equation AMD triple-S cooling equation

AMD triple-S for 12 Be α-α 3 fm • 0+1 -62. 14 Me. V, 0+2 -58. 33 Me. V • 1 - -57. 43 Me. V 0 - -54. 24 Me. V • <N> value for the 4 n is 5. 43 higher shell mixing • 0 - is much higher than second 0+ and 1 -, and it is considered that the observed state at 2. 24 Me. V must be the second 0+ state.

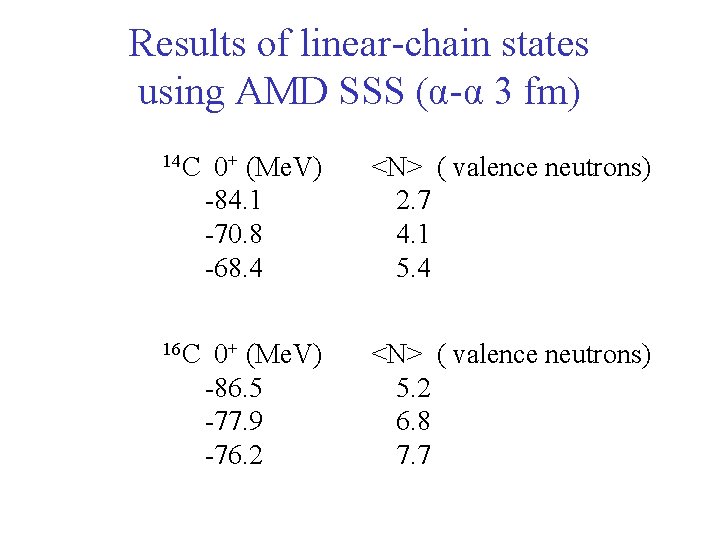
Results of linear-chain states using AMD SSS (α-α 3 fm) 14 C 0+ (Me. V) -84. 1 -70. 8 -68. 4 <N> ( valence neutrons) 2. 7 4. 1 5. 4 16 C 0+ (Me. V) -86. 5 -77. 9 -76. 2 <N> ( valence neutrons) 5. 2 6. 8 7. 7

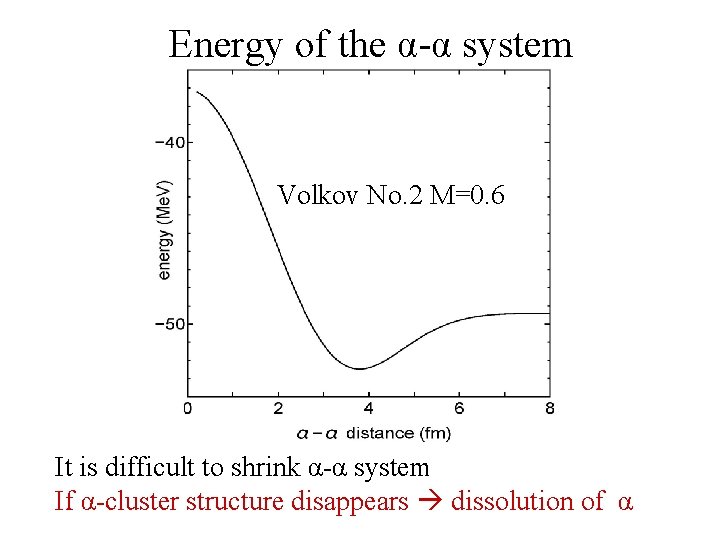
Energy of the α-α system Volkov No. 2 M=0. 6 It is difficult to shrink α-α system If α-cluster structure disappears dissolution of α

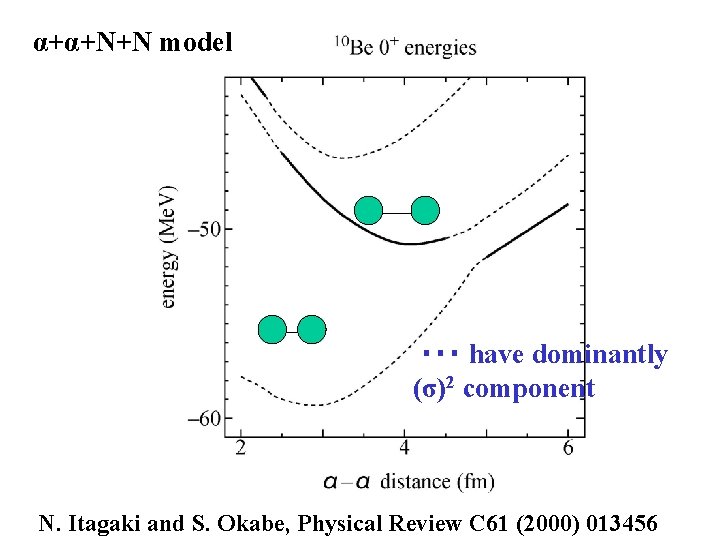
α+α+N+N model ・・・ have dominantly (σ)2 component N. Itagaki and S. Okabe, Physical Review C 61 (2000) 013456

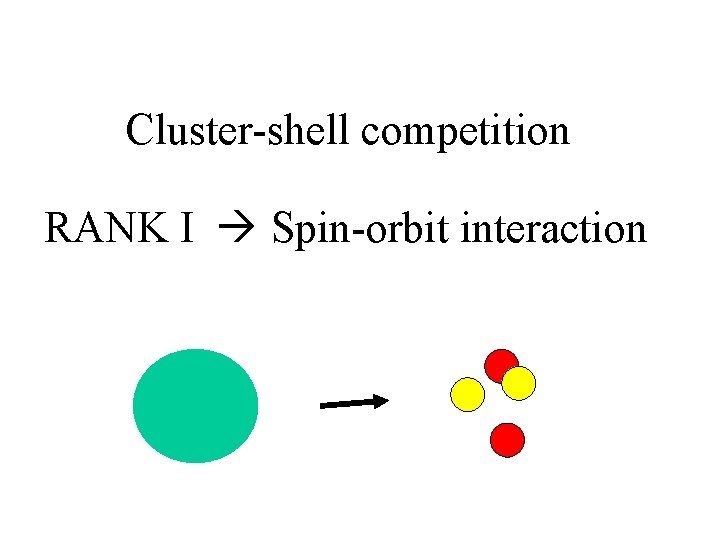
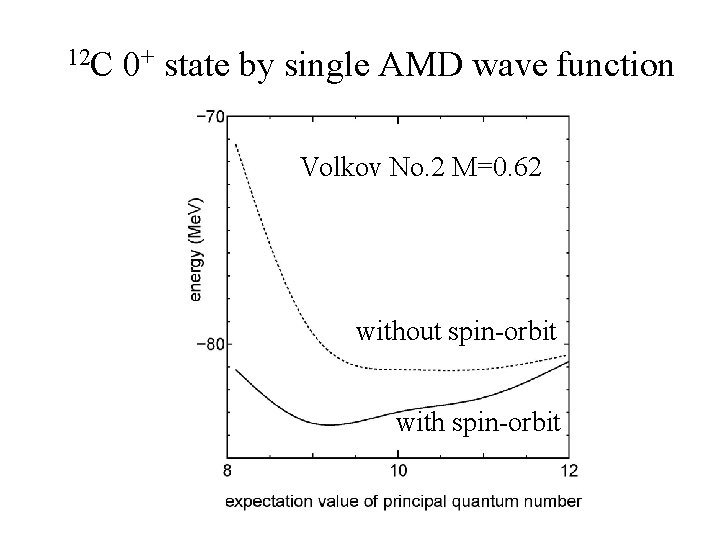
Cluster-shell competition RANK I Spin-orbit interaction

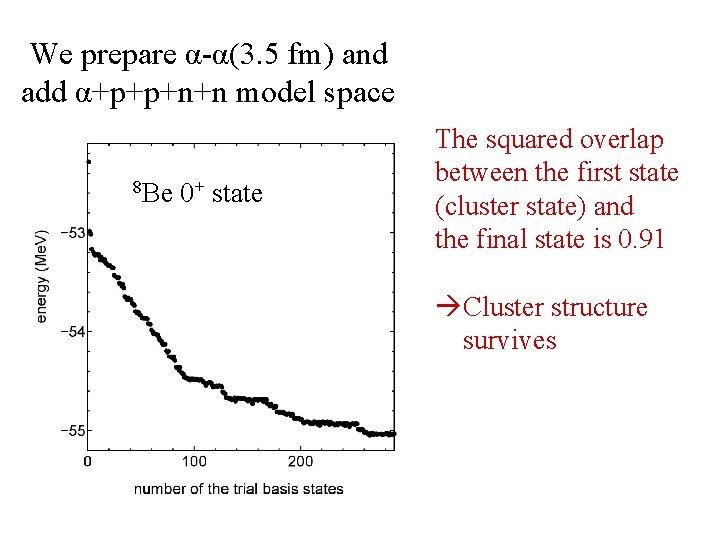
We prepare α-α(3. 5 fm) and add α+p+p+n+n model space 8 Be 0+ state The squared overlap between the first state (cluster state) and the final state is 0. 91 Cluster structure survives

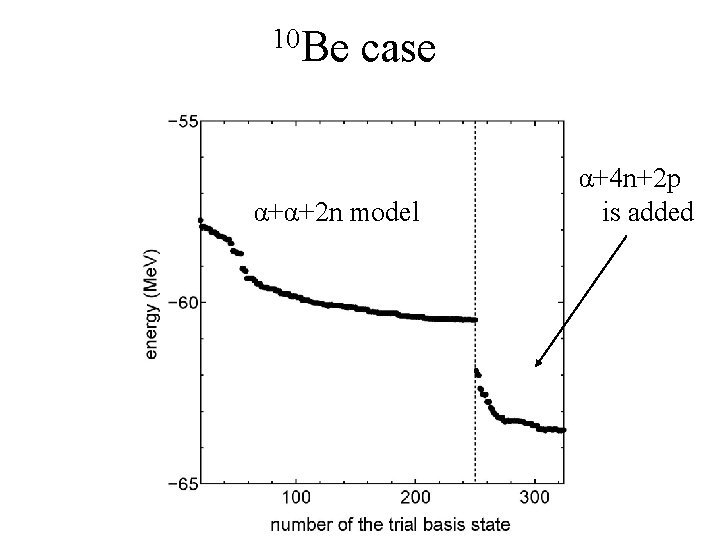
10 Be case α+α+2 n model 　α+α+n+n 　α+4 n+2 p is added

12 C 0+ state by single AMD wave function Volkov No. 2 M=0. 62 without spin-orbit with spin-orbit

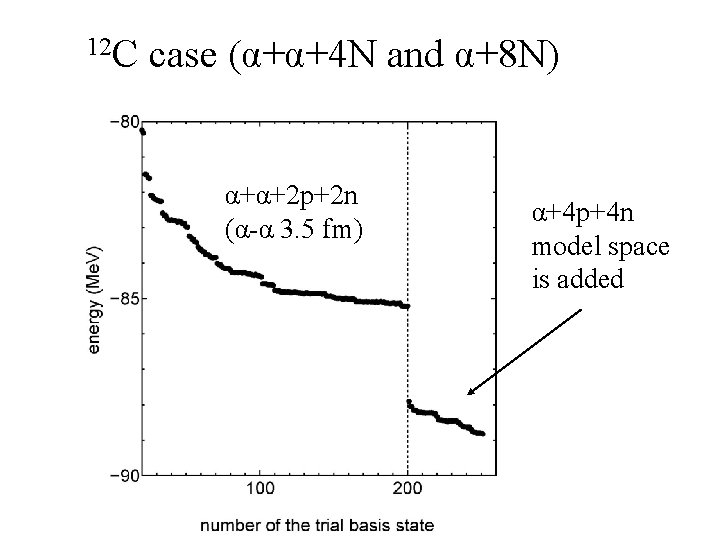
12 C case (α+α+4 N and α+8 N) α+α+2 p+2 n (α-α 3. 5 fm) α+4 p+4 n model space is added

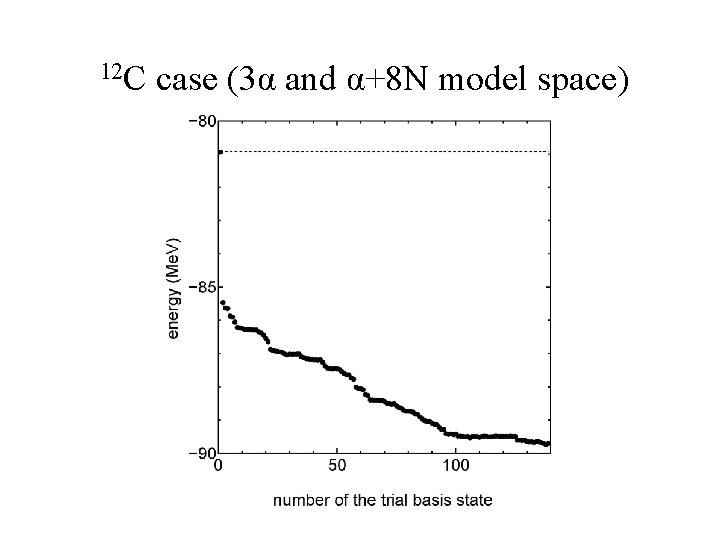
12 C case (3α and α+8 N model space)

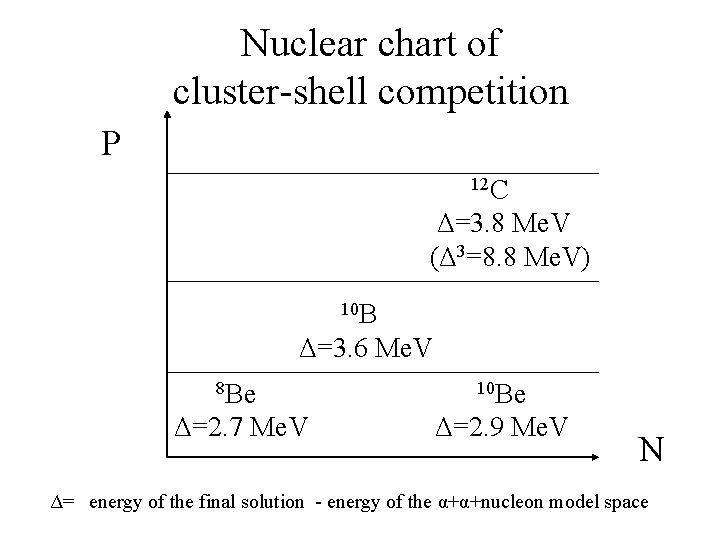
Nuclear chart of cluster-shell competition P 12 C Δ=3. 8 Me. V (Δ 3=8. 8 Me. V) 10 B Δ=3. 6 Me. V 8 Be 10 Be Δ=2. 7 Me. V Δ=2. 9 Me. V N Δ= energy of the final solution - energy of the α+α+nucleon model space

Cluster-shell competition RANK II Tensor interaction is renormalized in the central part and the spin orbit part This should be explicitly treated in weakly bound systems Already started by A. Dote, T. Myo, S. Sugimoto….

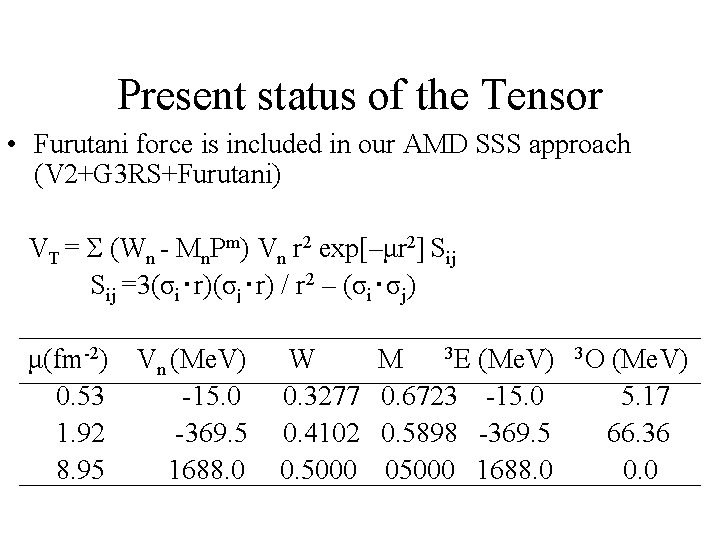
Present status of the Tensor • Furutani force is included in our AMD SSS approach (V 2+G 3 RS+Furutani) VT = Σ (Wn - Mn. Pm) Vn r 2 exp[–μr 2] Sij =3(σi・r)(σｊ・r) / r 2 – (σi・σj) μ(fm-2) 0. 53 1. 92 8. 95 Vn (Me. V) -15. 0 -369. 5 1688. 0 W 0. 3277 0. 4102 0. 5000 3 E (Me. V) M 0. 6723 -15. 0 0. 5898 -369. 5 05000 1688. 0 3 O (Me. V) 5. 17 66. 36 0. 0

Furutani force is included in our AMD SSS approach (V 2+G 3 RS+Furutani) For α, we generate 400 basis states and Sz = 0, 1 for the neutrons and Sz = 0, 1 for the protons are prepared. (Virtual Jacobi coordinate is introduced) Total (Me. V) T (Me. V) V (Me. V) LS (Me. V) Tenser (Me. V) N -37. 7 53. 5 -74. 6 0. 4 -17. 0 0. 35 (0 s)4 -27. 6 43. 8 -71. 3 0. 0

Simple description of α • We keep the spatial part as (s 1/2)4 -35. 57 Me. V by 30 Slater determinants • We use this simple description of α-cluster to 4 N nuclei

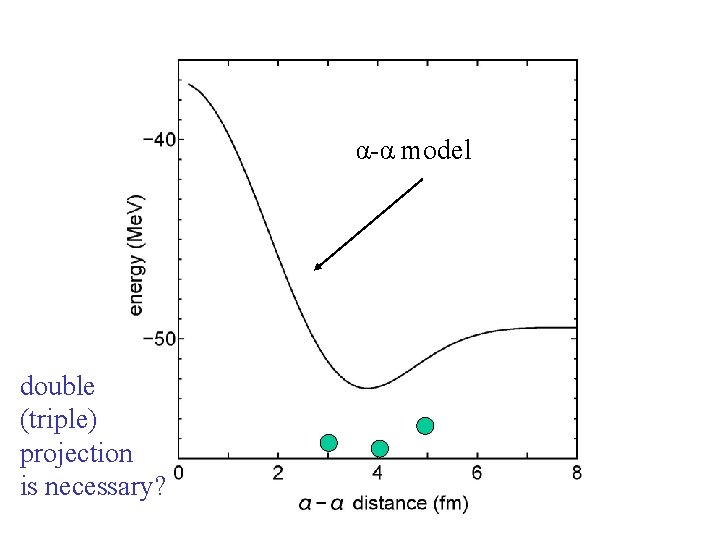
α-α model double (triple) projection is necessary?

12 C α-α 2. 5 fm • Without Tensor -85. 7 Me. V • With Tensor -90. 6 Me. V Double (triple) projection is necessary?

Conclusion • Molecular-orbit is a good tool to describe the cluster structure of neutron-rich nuclei. • To investigate heavier nuclei, we have introduced new AMD method (AMD triple-S), and the previous MO results are justified using large model space. • The spin-orbit interaction plays a crucial role for the cluster-shell competiton. • Tensor term is incorporated but we really need to fix the interaction.