CLUSTERS OF GALAXIES Lecture 1 Introduction and Structure

CLUSTERS OF GALAXIES Lecture 1 Introduction and Structure Formation

Clusters of Galaxies: a short overview

Clusters of Galaxies X-ray Band

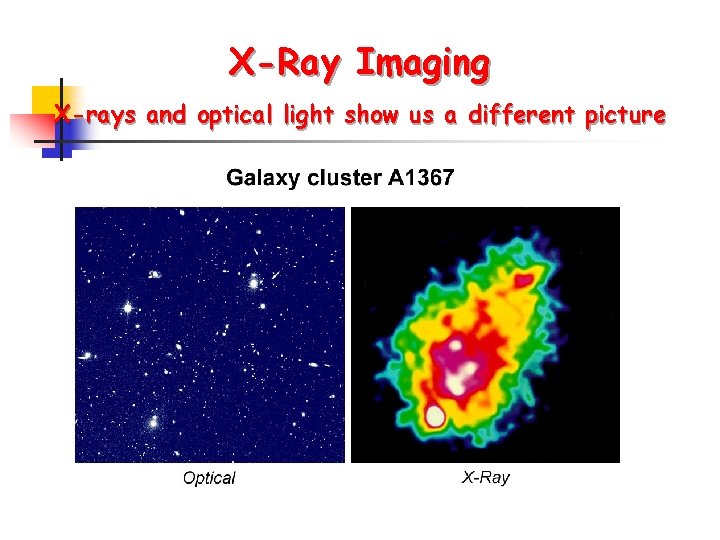
X-Ray Imaging X-rays and optical light show us a different picture

X-Ray Imaging X-rays and optical light show us a different picture

Why study Clusters n Clusters are the largest structures in the Universe to have clearly decoupled from the Hubble flow, they carry important cosmological information n Physical conditions in clusters are unlike anywhere else. They are laboratories where we can study the laws of physics under conditions unachiavable elsewhere.

The Physics of the ICM n Cool Cores n Cold Fronts n Metals & the ICM n Non-thermal processes in clusters

The Cluster-Cosmology connection n X-ray Luminosity function, X-ray Temperature function and their evolution n Scaling relations, entropy and baryonic fraction n Super-Clusters

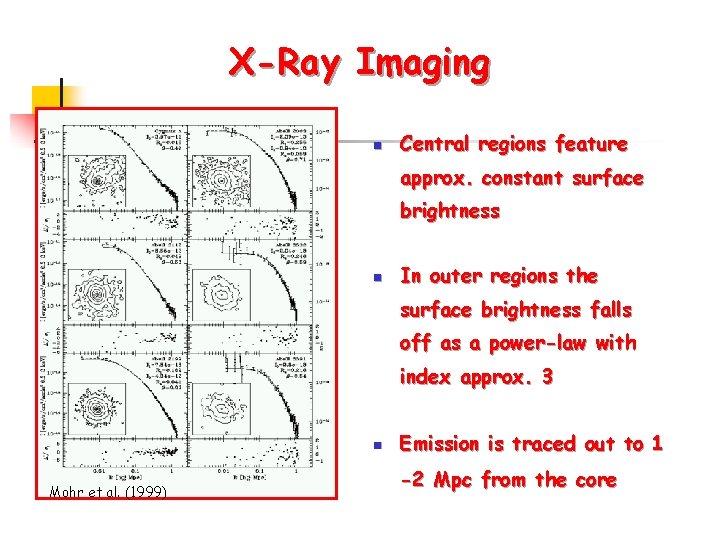
X-Ray Imaging n Central regions feature approx. constant surface brightness n In outer regions the surface brightness falls off as a power-law with index approx. 3 n Mohr et al. (1999) Emission is traced out to 1 -2 Mpc from the core

Principio Fondamentale della Cosmologia L’Universo e’ Omogeneo ed Isotropo Perche’ osserviamo le stelle, le galassie, gli ammassi di galassie? La struttura su larga scala si e’ formata per la crescita gravitazionale di piccole perturbazioni di densita’.

Structure Formation

Structure Formation

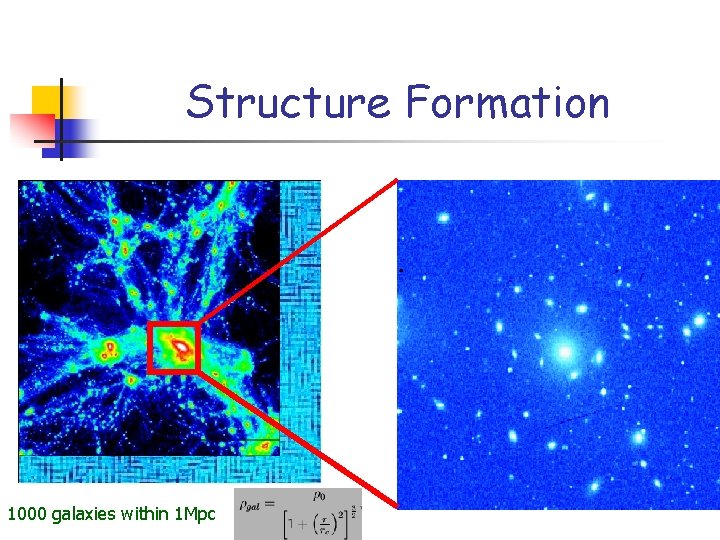
Structure Formation 1000 galaxies within 1 Mpc

Structure Formation Linear Theory Let us consider the density field with density fluctuations: This is subject to the continuity equations of Eulero and Poisson: Entropy conservation The system does not have a generic analytic solution. However we can linearize the Fourier transform of the previous system. In this case we have:

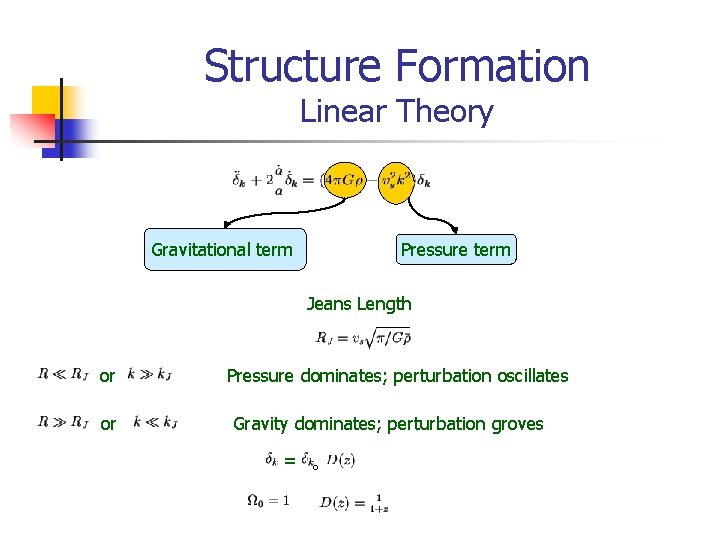
Structure Formation Linear Theory Gravitational term Pressure term Jeans Length or or Pressure dominates; perturbation oscillates Gravity dominates; perturbation groves = o

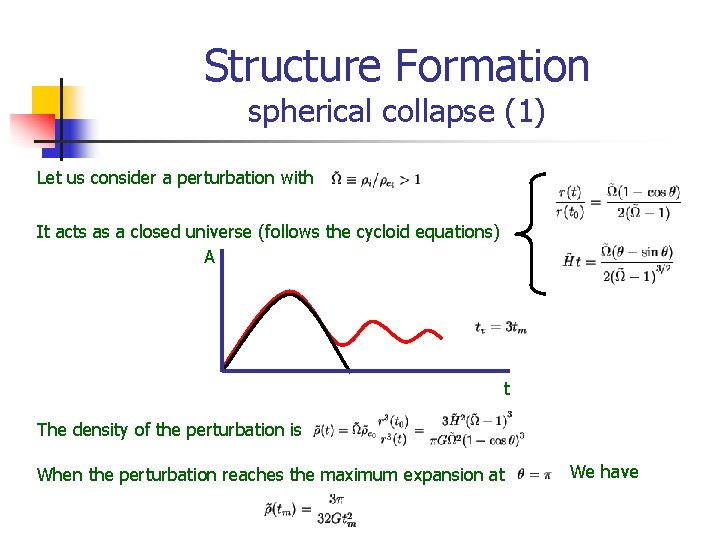
Structure Formation spherical collapse (1) Let us consider a perturbation with It acts as a closed universe (follows the cycloid equations) A t The density of the perturbation is When the perturbation reaches the maximum expansion at We have

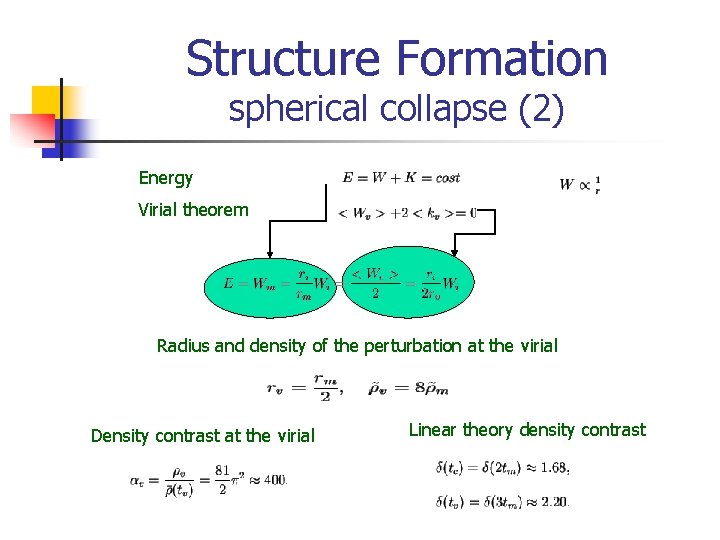
Structure Formation spherical collapse (2) Energy Virial theorem Radius and density of the perturbation at the virial Density contrast at the virial Linear theory density contrast

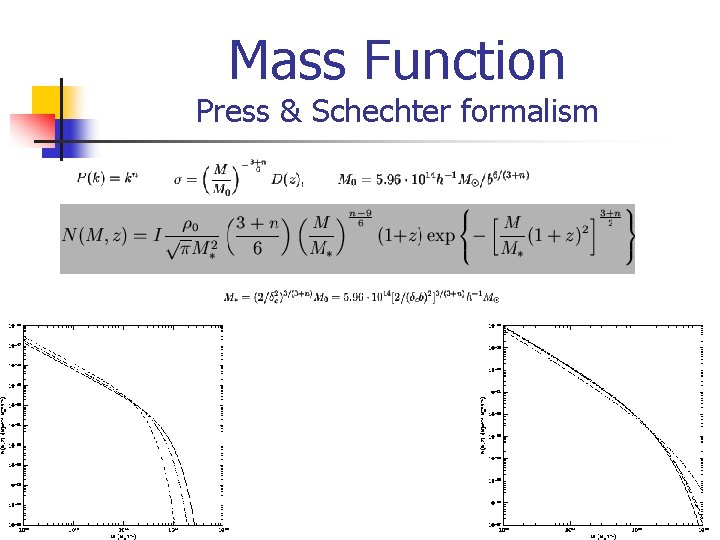
Mass Function Press & Schechter formalism Density of objects per unit of mass The press & Schechter formalism is WRONG It is simple and help to identify the main “topics” It gives also a simple analytic formula for the mass function It is based on the linear theory and uses only and

Mass Function Press & Schechter formalism We consider a density field smoothed on the scale The probability that the fluctuation or Is collapsed is given by where The number density is then Or equivalently

Mass Function Press & Schechter formalism

Intracluster Medium Hydrostatic equilibrium (spherical symmetry) We can measure the Cluster mass Dynamical Properties of the Galaxies Isothermal Cluster King profile Beta Profile