Clustering w Basic concepts with simple examples w

Clustering w Basic concepts with simple examples w Categories of clustering methods w Challenges 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 1

What is clustering? The process of grouping a set of physical or abstract objects into classes of similar objects. It is also called unsupervised learning. It is a common and important task that finds many applications n n Examples of clusters? Examples where we need clustering? 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 2

Differences from Classification How different? Which one is more difficult as a learning problem? Do we perform clustering in daily activities? How do we cluster? How to measure the results of clustering? n With/without class labels Between classification and clustering n Semi-supervised clustering 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 3

Major clustering methods Partitioning methods n k-Means (and EM), k-Medoids Hierarchical methods n agglomerative, divisive, BIRCH Similarity and dissimilarity of points in the same cluster and from different clusters Distance measures between clusters n minimum, maximum n Means of clusters n Average between clusters 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 4

Clustering -- Example 1 For simplicity, 1 -dimension objects and k=2. Objects: 1, 2, 5, 6, 7 K-means: n n n Randomly select 5 and 6 as centroids; => Two clusters {1, 2, 5} and {6, 7}; mean. C 1=8/3, mean. C 2=6. 5 => {1, 2}, {5, 6, 7}; mean. C 1=1. 5, mean. C 2=6 => no change. Aggregate dissimilarity = 0. 5^2 + 1^2 = 2. 5 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 5

Issues with k-means A heuristic method Sensitive to outliers n How to prove it? Determining k n n Trial and error X-means, PCA-based Crisp clustering n EM, Fuzzy c-means Not be confused with k-NN 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 6

Clustering -- Example 2 For simplicity, we still use 1 -dimension objects. Objects: 1, 2, 5, 6, 7 agglomerative clustering – a very frequently used algorithm How to cluster: n n find two closest objects and merge; => {1, 2}, so we have now {1. 5, 5, 6, 7}; => {1, 2}, {5, 6}, so {1. 5, 5. 5, 7}; => {1, 2}, {{5, 6}, 7}. 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 7

Issues with dendrograms How to find proper clusters An alternative: divisive algorithms n Top down w Comparing with bottom-up, which is more efficient n n What’s the time complexity? How to efficiently divide the data w A heuristic – Minimum Spanning Tree http: //en. wikipedia. org/wiki/Minimum_spanning_tree n 12/19/2021 What’s the time complexity CSE 572, CBS 572: Data Mining by H. Liu 8

Distance measures Single link n Measured by the shortest edge between the two clusters Complete link n Measured by the longest edge Average link n Measured by the average edge length An example is shown next. 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 9

An example to show different Links Single link n n Merge the nearest clusters measured by the shortest edge between the two (((A B) (C D)) E) Complete link n n Merge the nearest clusters measured by the longest edge between the two (((A B) E) (C D)) Average link n n A B C D E A 0 1 2 2 3 B 1 0 2 4 3 C 2 2 0 1 5 D 2 4 1 0 3 E 3 3 5 3 0 B A Merge the nearest clusters measured by the average edge length between E the two (((A B) (C D)) E) C D 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 10

Other Methods Density-based methods n DBSCAN: a cluster is a maximal set of density-connected points w Core points defined using epsilon-neighborhood and min. Pts w Apply directly density reachable (e. g. , P and Q, Q and M) and density-reachable (P and M, assuming so are P and N), and densityconnected (any density reachable points, P, Q, M, N) form clusters Grid-based methods n STING: the lowest level is the original data w statistical parameters of higher-level cells are computed from the parameters of the lower-level cells (count, mean, standard deviation, min, max, distribution Model-based methods n Conceptual clustering: COBWEB w Category utility w Intraclass similarity w Interclass dissimilarity 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 11

Density-based DBSCAN – Density-Based Clustering of Applications with Noise It grows regions with sufficiently high density into clusters and can discover clusters of arbitrary shape in spatial databases with noise. n Many existing clustering algorithms find spherical shapes of clusters DEBSCAN defines a cluster as a maximal set of density-connected points. Density is defined by an area and # of points 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 12
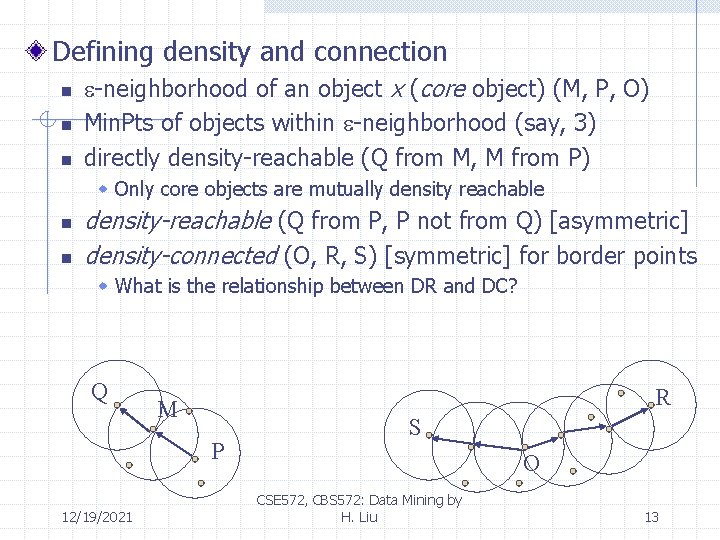
Defining density and connection n -neighborhood of an object x (core object) (M, P, O) Min. Pts of objects within -neighborhood (say, 3) directly density-reachable (Q from M, M from P) w Only core objects are mutually density reachable n n density-reachable (Q from P, P not from Q) [asymmetric] density-connected (O, R, S) [symmetric] for border points w What is the relationship between DR and DC? Q R M P 12/19/2021 S O CSE 572, CBS 572: Data Mining by H. Liu 13

Clustering with DBSCAN n n Search for clusters by checking the -neighborhood of each instance x If the -neighborhood of x contains more than Min. Pts, create a new cluster with x as a core object Iteratively collect directly density-reachable objects from these core object and merge density-reachable clusters Terminate when no new point can be added to any cluster DBSCAN is sensitive to the thresholds of density, but it is fast Time complexity O(N log N) if a spatial index is used, O(N 2) otherwise 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 14

Neural networks n Self-organizing feature maps (SOMs) Subspace clustering n n Clique: if a k-dimensional unit space is dense, then so are its (k-1)-d subspaces More will be discussed later Semi-supervised clustering http: //www. cs. utexas. edu/~ml/publication/unsupervised. html http: //www. cs. utexas. edu/users/ml/risc/ 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 15

Challenges Scalability Dealing with different types of attributes Clusters with arbitrary shapes Automatically determining input parameters Dealing with noise (outliers) Order insensitivity of instances presented to learning High dimensionality Interpretability and usability 12/19/2021 CSE 572, CBS 572: Data Mining by H. Liu 16
- Slides: 16