Clustering of Maintenance Tasks for the Danish Railway

Clustering of Maintenance Tasks for the Danish Railway System The International Conference on Intelligent Systems Design and Applications (ISDA) SHAHRZAD M. POUR AND UNA BENLIC

Introduction The European Rail Traffic Management System (ERTMS) is a major ongoing European industrial project that aims to standardize rail traffic signaling that will lead to faster travel within the EU. Denmark will be the first country to upgrade its entire signaling system to the ERTMS standards.

Problem definition Industrial need for defining sub-regions workload needs to be fairly distributed across sub-regions The geographic position of the maintenance points (tasks) should ensure that crew members can travel from one task to another quickly

Mathematical model The problem of allocating maintenance tasks to the maintenance team of a railway system can be viewed as an instance of the Generalized Assignment Problem (GAP). The objective of the proposed model is the minimization of the following three criteria: • (i) the total distance traveled from depots to tasks (as defined in Eq. 1), • (ii) the maximal distance between any maintenance task and its allocated crew member, • (iii) the imbalance in workload among crew members.

Experimental results The proposed model, as well as the GAP model used for comparisons, is coded in GAMS and executed on a machine equipped with Intel (R) Core (TM) i 7 -4600 U CPU at 2. 10 GHz and 8 GB of RAM. We use the default setting for GAMS, i. e. , optca = 0: 0 and optcr = 0: 1. Benchmark instances Rail tracks of the maintenance area. Instances from this class are prefixed with `E'; Mixture of on-tack or out-track positions within the maintenance area. Instances from this class are prefixed with `M'; Scattered at random positions around the entire Jutland region. Instances from this class are prefixed with `R'.

Sample of Benchmark instances

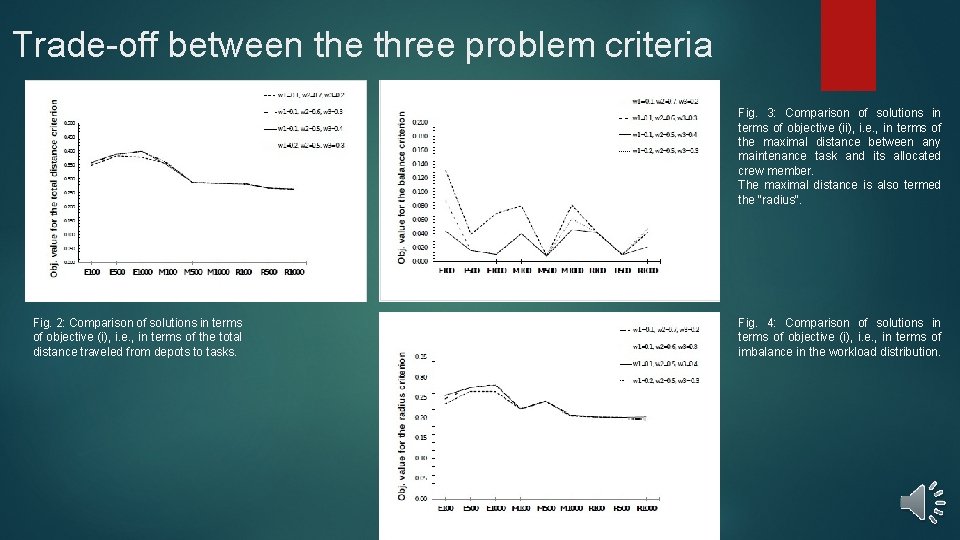
Trade-off between the three problem criteria Problem objectives: • (i) the total distance traveled from depots to tasks, • (ii) the maximal distance between any maintenance task and its allocated crew member, • (iii) the imbalance in workload among crew members. Priorities: • Objective (ii), followed by objectives (iii) and (i). To analyze the trade-o in terms of the three criteria, we try four different combinations of the corresponding weight coefficients such that w 2 >= w 3 >= w 1, where w 1; w 2; w 3 2 [0; 1]. Normalization: • The objective values associated to each individual criterion to take on a value in the range [0; 1] is normalized.

Trade-off between the three problem criteria Fig. 3: Comparison of solutions in terms of objective (ii), i. e. , in terms of the maximal distance between any maintenance task and its allocated crew member. The maximal distance is also termed the “radius". Fig. 2: Comparison of solutions in terms of objective (i), i. e. , in terms of the total distance traveled from depots to tasks. Fig. 4: Comparison of solutions in terms of objective (i), i. e. , in terms of imbalance in the workload distribution.

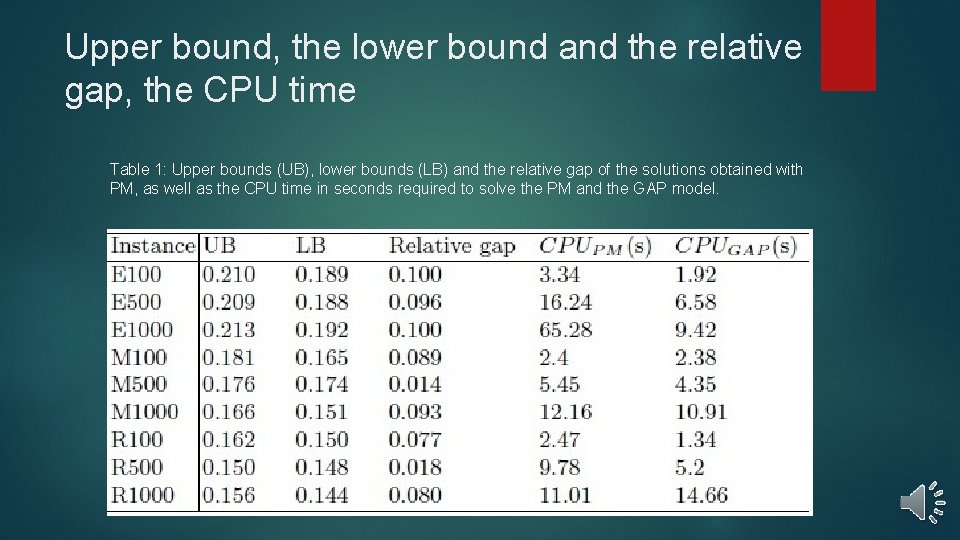
Upper bound, the lower bound and the relative gap, the CPU time Table 1: Upper bounds (UB), lower bounds (LB) and the relative gap of the solutions obtained with PM, as well as the CPU time in seconds required to solve the PM and the GAP model.

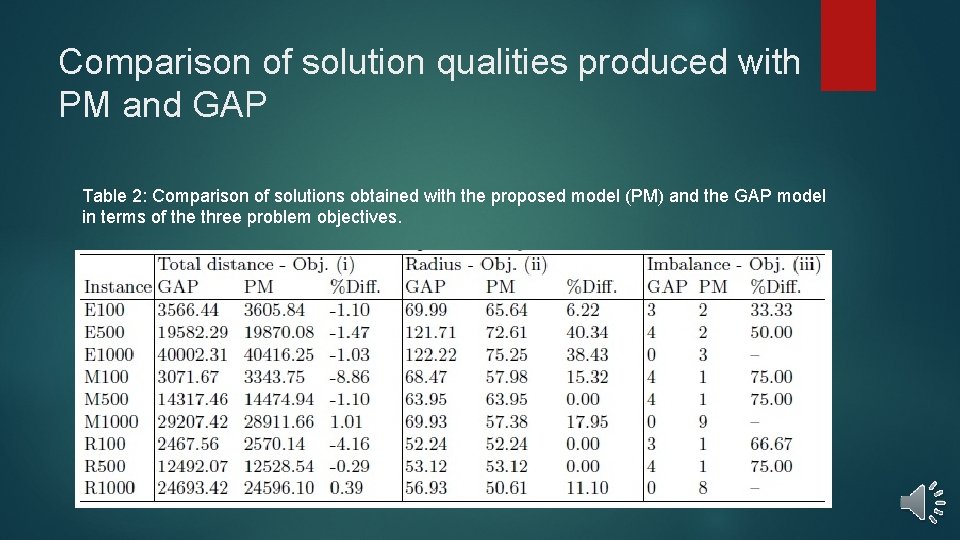
Comparison of solution qualities produced with PM and GAP Table 2: Comparison of solutions obtained with the proposed model (PM) and the GAP model in terms of the three problem objectives.

Conclusion A mathematical model for partitioning a spatial area into sub regions considering the geographical locations of the Danish railway network is proposed. The problem consists of determining which tasks are served by which depots, prior to the routing and scheduling phase, by taking into account the specific requirements to deal with failures and breakdown of the railway network. A mathematical model that optimizes the three problem criteria, and applied it on a set of instances that simulate the distribution of tasks in the Jutland peninsula, the largest region of Denmark is presented. Due to speciation of Danish railway network, maintenance scheduling can be seen as a Multi Depot Vehicle Routing Problem (MDVRP. This model can be considered as the clustering phase of MDVRP.

References 1. Barger, P. , Schon, W. , Bouali, M. : A study of railway ERTMS safety with Colored Petri Nets. In: Proceedings of the European Safety and Reliability Conference (ESREL 09), vol. 2, 1303{1309 (2009) 2. Patra, A. P. , Dersin, P. , Kumar, U. : Cost ective maintenance policy - A case study, International Journal of Performability Engineering 6(6), 595{603 (2010) 3. Banedanmark. , Trakministeriet. : The signalling programme - a total renewal of the Danish signalling infrastructure, Banedanmark (2009) 4. Lenstra, J. , Kan, A. : Complexity of vehicle routing and scheduling problems, Networks 11(2), 221{227 (1981) 5. Shmoys, D. B. , Tardos, E. : An approximation algorithm for the generalized assignment problem. Math. Program 62(3), 461{474 (1993) 6. Montoya-Torres, J. R. , Franco, J. L. , Isaza, S. N. , Jimenez, H. F. , Herazo-Padilla, N. : A literature review on the vehicle routing problem with multiple depots, Computers and Industrial Engineering 79, 115{129 (2015) 7. Giosa, I. , Tansini, I. , Viera, I. : New assignment algorithms for the multidepot vehicle routing problem, Journal of the Operational Research Society 52(5), 977{984 (2001) 8. Cordeau, J. , Laporte, G. , Mercier, A. : A unied tabu search heuristic for vehicle routing problems with time windows, Journal of the Operational Research Society 52(8), 928{936 (2001) 9. Pisinger, D. , Ropke, S. : A general heuristic for vehicle routing problems, Computers and Operations Research 34(8), 2403{2435 (2007)