Clustering Methods Part 2 a Kmeans algorithm Pasi





- Slides: 10

Clustering Methods: Part 2 a K-means algorithm Pasi Fränti Speech and Image Processing Unit School of Computing University of Eastern Finland

K-means overview • Well-known clustering algorithm • Number of clusters must be chosen in advance • Strengths: 1. Vectors can flexibly change clusters during the process. 2. Always converges to a local optimum. 3. Quite fast for most applications. • Weaknesses: 1. Quality of the output depends on the initial codebook. 2. Global optimum solution not guaranteed.

K-means pseudo code X: a set of N data vectors Data set CI: initialized k cluster centroids Number of clusters, C: the cluster centroids of k-clustering random initial centroids P = {p(i) | i = 1, …, N} is the cluster label of X KMEANS(X, CI) → (C, P) REPEAT Cprevious ← CI; FOR all i ∈ [1, N] DO p(i) ← arg min d(xi, cj); Generate new optimal paritions l≤j≤k FOR all j ∈ [1, k] DO cj ← Average of xi, whose p(i) = j; UNTIL C = Cprevious Generate optimal centroids

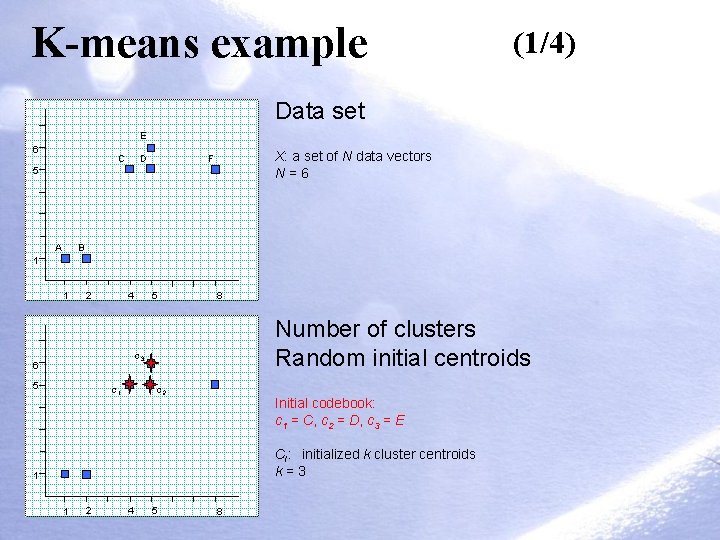
K-means example (1/4) Data set E 6 C D X: a set of N data vectors N=6 F 5 A B 1 1 2 4 5 8 Number of clusters Random initial centroids c 3 6 5 c 1 c 2 Initial codebook: c 1 = C, c 2 = D, c 3 = E CI: initialized k cluster centroids k=3 1 1 2 4 5 8

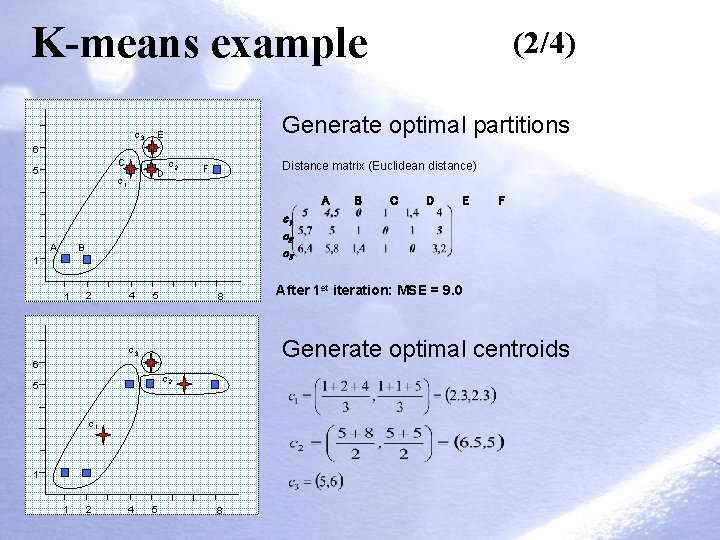
K-means example c 3 (2/4) Generate optimal partitions E 6 C 5 D c 1 c 2 Distance matrix (Euclidean distance) F A A 1 2 4 5 8 D E F 6 c 2 5 c 1 1 2 4 After 1 st iteration: MSE = 9. 0 Generate optimal centroids c 3 1 C c 1 c 2 c 3 B 1 B 5 8

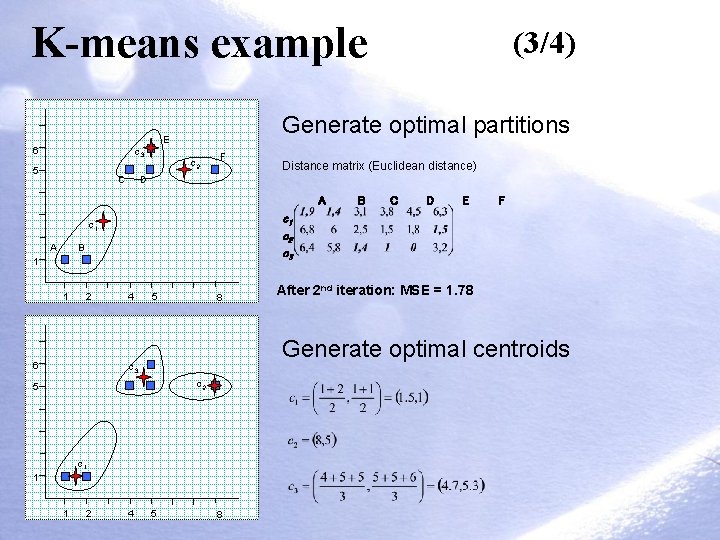
K-means example Generate optimal partitions E 6 c 3 5 C c 2 F Distance matrix (Euclidean distance) D A B 1 1 2 6 4 5 8 c 2 5 c 1 1 2 C D E F 4 After 2 nd iteration: MSE = 1. 78 Generate optimal centroids c 3 1 B c 1 c 2 c 3 c 1 A (3/4) 5 8

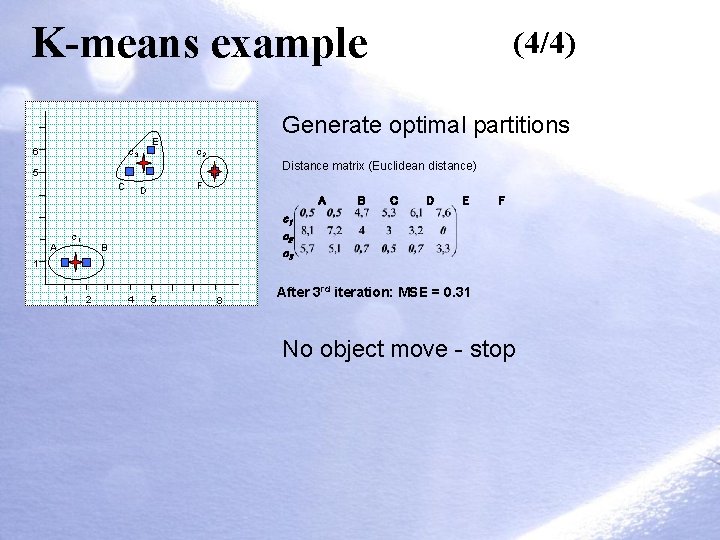
K-means example E c 3 6 (4/4) Generate optimal partitions c 2 Distance matrix (Euclidean distance) 5 C c 1 A F D A B 2 C D E F c 1 c 2 c 3 1 1 B 4 5 8 After 3 rd iteration: MSE = 0. 31 No object move - stop

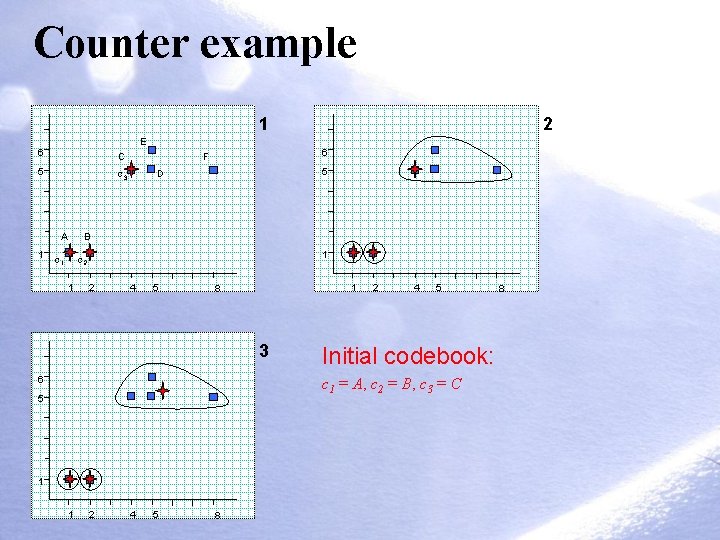
Counter example 1 2 E 6 C 5 c 3 A 1 c 1 6 F 5 D B 1 c 2 1 2 4 5 1 8 3 6 2 4 5 Initial codebook: c 1 = A, c 2 = B, c 3 = C 5 1 1 2 4 5 8 8

Two ways to improve k-means • Repeated k-means – Try several random initializations and take the best. – Multiplies processing time. – Works for easier data sets. • Better initialization – Use some better heuristic to allocate the initial distribution of code vectors. – Designing good initialization is not any easier than designing good clustering algorithm at the first place! – K-means can (and should) anyway be applied as finetuning of the result of another method.

References 1. Forgy, E. W. (1965) Cluster analysis of multivariate data: efficiency vs interpretability of classifications. Biometrics 21, 768 -769. 2. Mc. Queen, J. (1967) Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, eds L. M. Le Cam & J. Neyman, 1, pp. 281 -297. Berkeley, CA: University of California Press. 3. Hartigan, J. A. and Wong, M. A. (1979). A K-means clustering algorithm. Applied Statistics 28, 100 -108. 4. Xu, M. : K-Means Based Clustering And Context Quantization. University of Joensuu, Computer Science, Academic Dissertation, 2005.