Clustering Linear and Nonlinear Manifolds using Generalized Principal

Clustering Linear and Nonlinear Manifolds using Generalized Principal Components Analysis René Vidal Center for Imaging Science Institute for Computational Medicine Johns Hopkins University

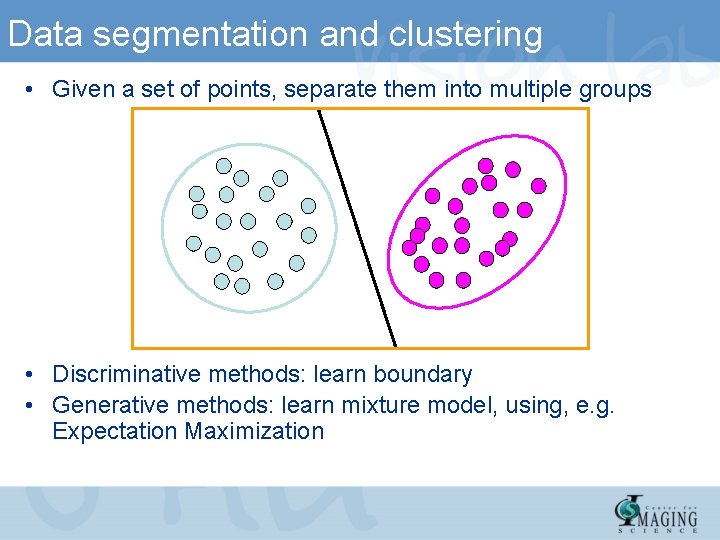
Data segmentation and clustering • Given a set of points, separate them into multiple groups • Discriminative methods: learn boundary • Generative methods: learn mixture model, using, e. g. Expectation Maximization

Dimensionality reduction and clustering • In many problems data is high-dimensional: can reduce dimensionality using, e. g. Principal Component Analysis • Image compression • Recognition – Faces (Eigenfaces) • Image segmentation – Intensity (black-white) – Texture

Clustering data on non Euclidean spaces • Clustering data on non Euclidean spaces – Mixtures of linear spaces – Mixtures of algebraic varieties – Mixtures of Lie groups • “Chicken-and-egg” problems – Given segmentation, estimate models – Given models, segment the data – Initialization? • Need to combine – Algebra/geometry, dynamics and statistics

Part I Linear Subspaces

Principal Component Analysis (PCA) • Given a set of points x 1, x 2, …, x. N – Geometric PCA: find a subspace S passing through them – Statistical PCA: find projection directions that maximize the variance • Solution (Beltrami’ 1873, Jordan’ 1874, Hotelling’ 33, Eckart-Householder-Young’ 36) Basis for S • Applications: data compression, regression, computer vision (eigenfaces), pattern recognition, genomics

Generalized Principal Component Analysis • Given a set of points lying in multiple subspaces, identify – The number of subspaces and their dimensions – A basis for each subspace – The segmentation of the data points • “Chicken-and-egg” problem – Given segmentation, estimate subspaces – Given subspaces, segment the data

Basic ideas behind GPCA • Towards an analytic solution to subspace clustering – Can we estimate ALL models simultaneously using ALL data? – When can we do so analytically? In closed form? – Is there a formula for the number of models? • Will consider the most general case – Subspaces of unknown and possibly different dimensions – Subspaces may intersect arbitrarily (not only at the origin) • GPCA is an algebraic geometric approach to data segmentation – Number of subspaces = degree of a polynomial – Subspace basis = derivatives of a polynomial – Subspace clustering is algebraically equivalent to • Polynomial fitting • Polynomial differentiation

Introductory example: algebraic clustering in 1 D • Number of groups?

Introductory example: algebraic clustering in 1 D • How to compute n, c, b’s? – Number of clusters – Cluster centers – Solution is unique if – Solution is closed form if

Introductory example: algebraic clustering in 2 D • What about dimension 2? • What about higher dimensions? – Complex numbers in higher dimensions? – How to find roots of a polynomial of quaternions? • Instead – Project data onto one or two dimensional space – Apply same algorithm to projected data

Representing one subspace • One plane • One line • One subspace can be represented with – Set of linear equations – Set of polynomials of degree 1

Representing n subspaces • Two planes • One plane and one line – Plane: – Line: De Morgan’s rule • A union of n subspaces can be represented with a set of homogeneous polynomials of degree n

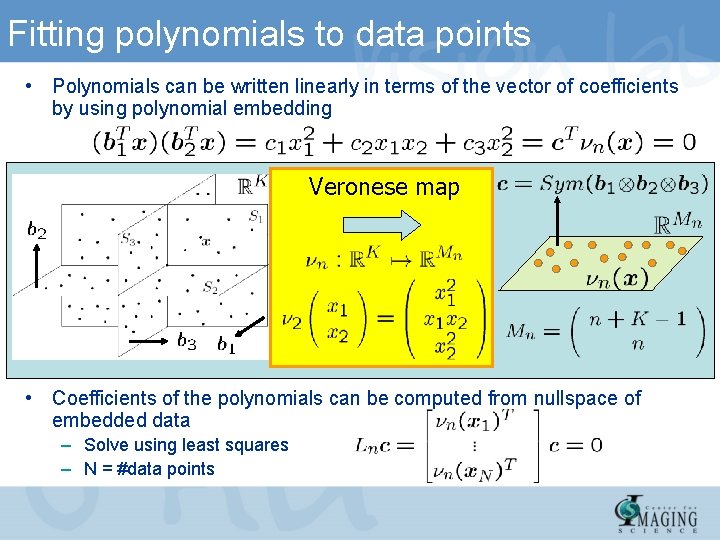
Fitting polynomials to data points • Polynomials can be written linearly in terms of the vector of coefficients by using polynomial embedding Veronese map • Coefficients of the polynomials can be computed from nullspace of embedded data – Solve using least squares – N = #data points

Finding a basis for each subspace Polynomial Differentiation (GPCA-PDA) [CVPR’ 04] • To learn a mixture of subspaces we just need one positive example per class

Choosing one point per subspace • With noise and outliers – Polynomials may not be a perfect union of subspaces – Normals can estimated correctly by choosing points optimally • Distance to closest subspace without knowing segmentation?

GPCA for hyperplane segmentation • Coefficients of the polynomial can be computed from null space of embedded data matrix – Solve using least squares – N = #data points • Number of subspaces can be computed from the rank of embedded data matrix • Normal to the subspaces from the derivatives of the polynomial can be computed

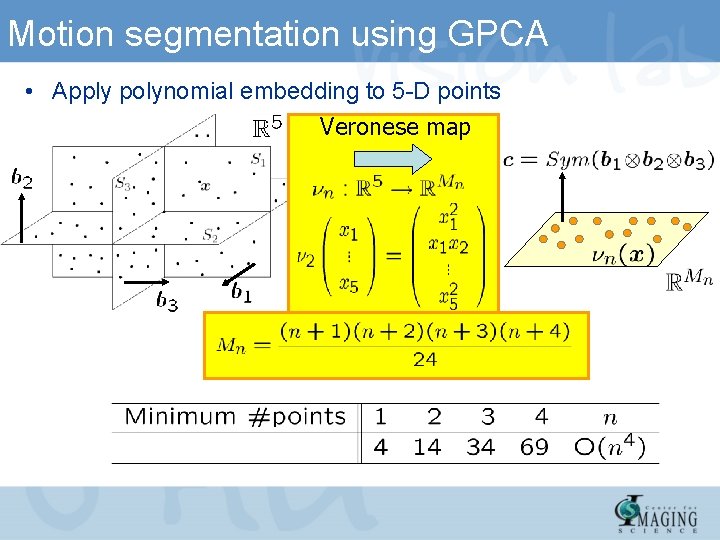
Motion segmentation using GPCA • Apply polynomial embedding to 5 -D points Veronese map

Experimental results: Kanatani sequences • Sequence A Sequence B • Percentage of correct classification Sequence C

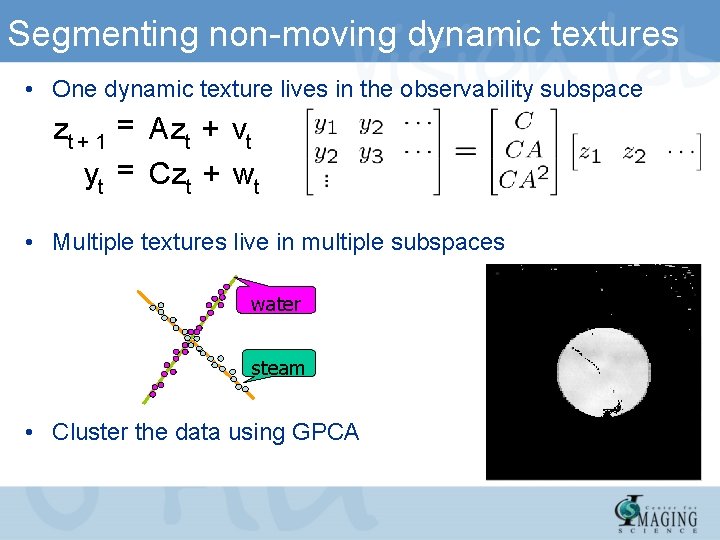
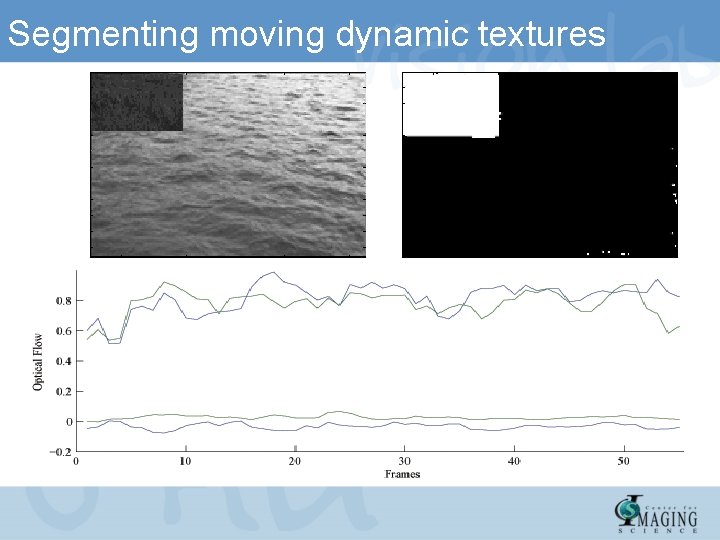
Segmenting non-moving dynamic textures • One dynamic texture lives in the observability subspace zt + 1 = Azt + vt yt = Czt + wt • Multiple textures live in multiple subspaces water steam • Cluster the data using GPCA

Segmenting moving dynamic textures

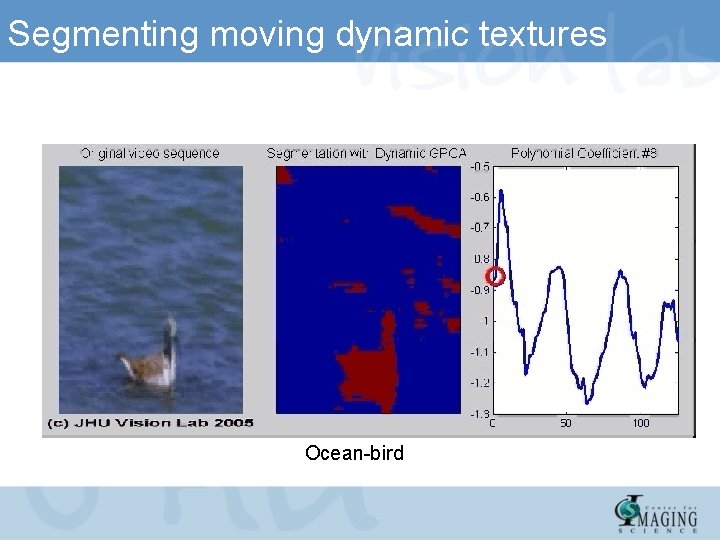
Segmenting moving dynamic textures Ocean-bird

Temporal video segmentation • Segmenting N=30 frames of a sequence containing n=3 scenes – Host – Guest – Both • Image intensities are output of linear system • xt + 1 = Axdynamics t + vt ytfit=n=3 Apply GPCA to Cxt + wt images observability subspaces appearance

Temporal video segmentation • Segmenting N=60 frames of a sequence containing n=3 scenes – Burning wheel – Burnt car with people – Burning car • Image intensities are output of linear system • xt + 1 = Axdynamics t + vt ytfit=n=3 Apply GPCA to Cxt + wt images observability subspaces appearance

Part 2 Submanifolds in Riemannian Spaces

Overview of our approach • Propose a novel framework for simultaneous dimensionality reduction and clustering of data lying in different submanifolds of a Riemannian space. • Extend nonlinear dimensionality reduction techniques from one submanifold of to m submanifolds of a Riemannian space. • Show that when the different submanifolds are separated, all the points from one connected submanifold can be mapped to a single point in a lowdimensional space.

Nonlinear Dimensionality Reduction • Two kinds of dimensionality reduction: global and local techniques. • Global techniques – preserve global properties of the data lying on a submanifold – similar to PCA for a linear subspace – Eg: ISOMAP and Kernel PCA • Local techniques – preserve local properties, obtained from the small neighborhoods around the datapoints. – also retain the global properties of the data – Eg: Locally Linear Embedding (LLE), Laplacian Eigenmaps, Hessian LLE

Local Nonlinear Dimensionality Reduction • We show that segmentation of the data can be obtained from the null space of a matrix built from the local representation, using local NDR. • When the different submanifolds are separated, – there is a mapping from all the points in one connected submanifold to a single point in the low-dimensional space. – effectively reduces to a standard central clustering problem. • We will illustrate using Locally Linear Embedding (LLE).

Local Nonlinear Dimensionality Reduction • Focus on local NDR methods. Each method operates in a similar manner as follows: • Step 1: Find the k-nearest neighbors of each data point according to the Euclidean distance • Step 2: Compute a matrix , that depends on the weights. represents the local geometry of the data points and incorporates reconstruction cost function in low dimension. • Step 3: Solve a sparse eigenvalue problem on matrix. The first eigenvector is the constant vector corresponding to eigenvalue 0.

Extending LLE to Riemannian Manifolds • Information about the local geometry of the manifold is essential only in the first two steps of each algorithm, modifications are made only to these two stages. • Key issues: – how to select the k. NN • by incorporating the Riemannian distance – how to compute the matrix the new metric. representing the local geometry using

Extending LLE to Riemannian Manifolds • LLE involves writing each data point as a linear combination of its neighbors. – Euclidean case, simply a least-squares problem – Riemannian case: one needs to solve an interpolation problem on the manifold. • How should the data points be interpolated? • What cost function should be minimized?

Clustering on Riemannian Manifolds • If the data lie in a disconnected union of k-connected submanifolds, the matrix is block-diagonal with blocks. • When the assumption of separated submanifolds is violated, we have and , respectively. • Hence, we can cluster the data into groups by applying k-means to the columns of a matrix whose rows are the eigenvectors in the null space of.

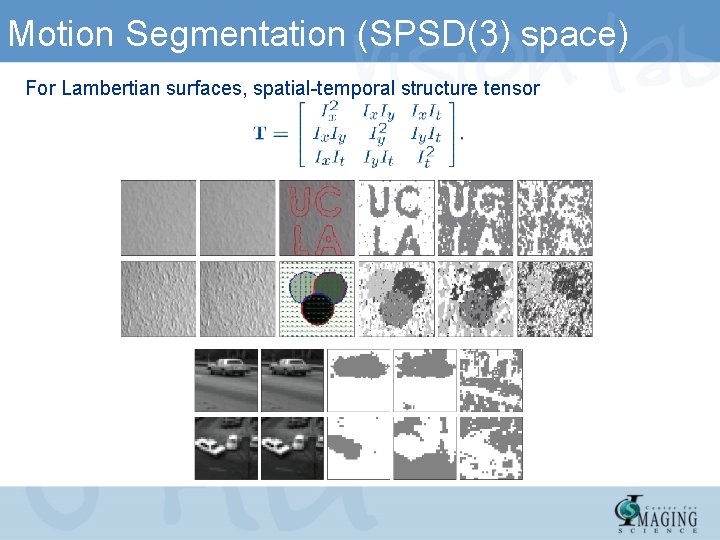
Motion Segmentation (SPSD(3) space) For Lambertian surfaces, spatial-temporal structure tensor

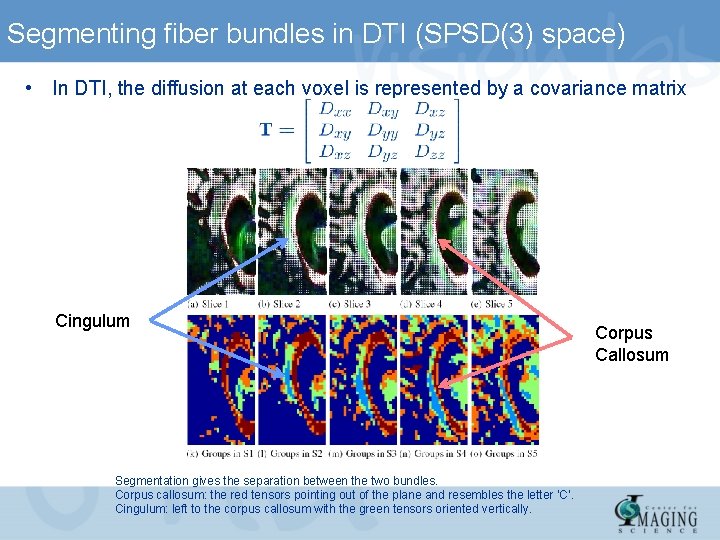
Segmenting fiber bundles in DTI (SPSD(3) space) • In DTI, the diffusion at each voxel is represented by a covariance matrix Cingulum Segmentation gives the separation between the two bundles. Corpus callosum: the red tensors pointing out of the plane and resembles the letter ‘C’. Cingulum: left to the corpus callosum with the green tensors oriented vertically. Corpus Callosum

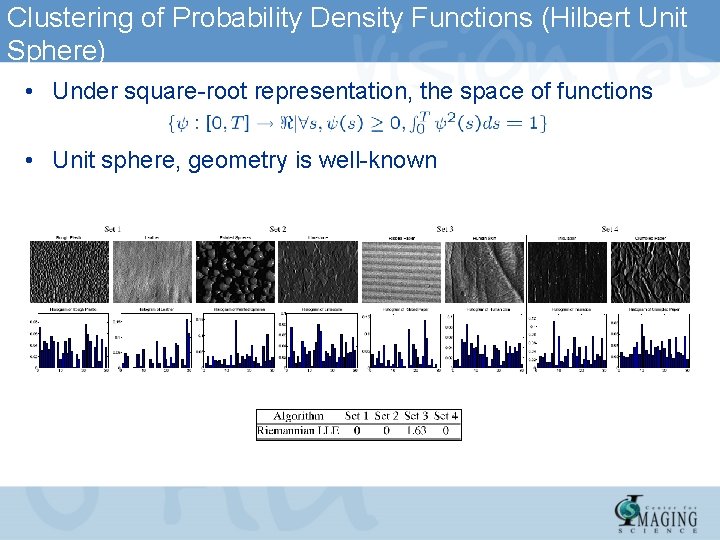
Clustering of Probability Density Functions (Hilbert Unit Sphere) • Under square-root representation, the space of functions • Unit sphere, geometry is well-known

Summary and Future Work

For more information, Vision, Dynamics and Learning Lab @ Johns Hopkins University Thank You!