Clustering kMeans hierarchical clustering SelfOrganizing Maps Outline kmeans

Clustering k-Means, hierarchical clustering, Self-Organizing Maps

Outline • • • k-means clustering Hierarchical clustering Self-Organizing Maps

Classification vs. Clustering Classification: Supervised learning

Classification vs. Clustering labels unknown Clustering: Unsupervised learning No labels, find “natural” grouping of instances

Many Clustering Applications! • Basically, everywhere labels are unknown/uncertain/too expensive • Marketing: find groups of similar customers • Astronomy: find groups of similar stars, galaxies • Earthquake studies: cluster earth quake epicenters along continent faults • Genomics: find groups of genes with similar expressions

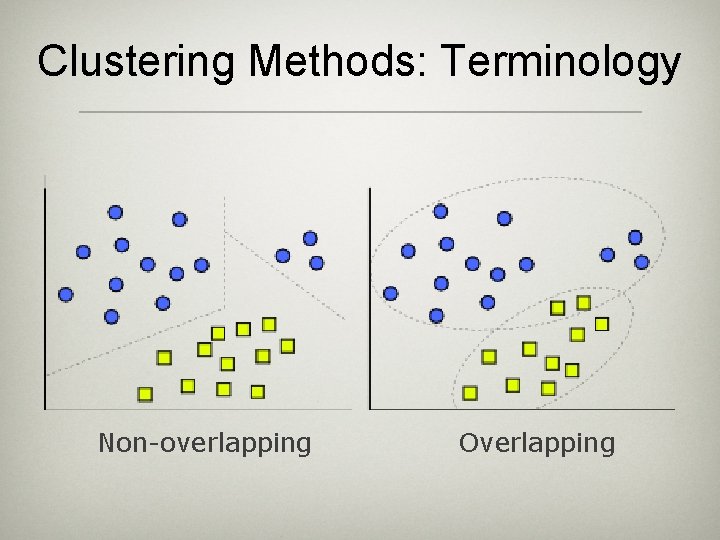
Clustering Methods: Terminology Non-overlapping Overlapping

Clustering Methods: Terminology Top-down Bottom-up (agglomerative)

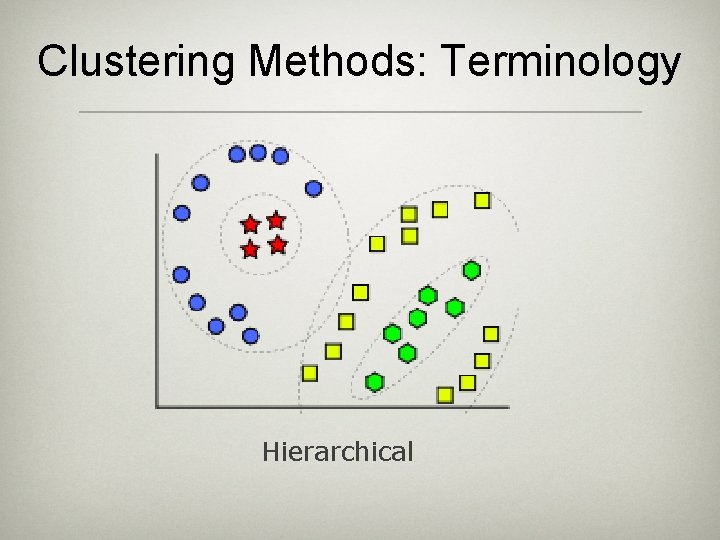
Clustering Methods: Terminology Hierarchical

Clustering Methods: Terminology Deterministic Probabilistic

k-Means Clustering

K-means clustering (k=3) k 1 y k 2 k 3 x Pick k random points: initial cluster centers

K-means clustering (k=3) k 1 y k 2 k 3 x Assign each point to nearest cluster center

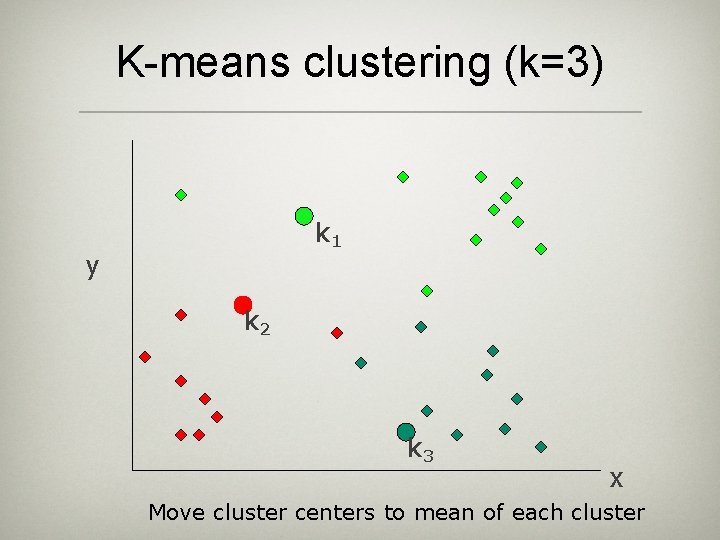
K-means clustering (k=3) k 1 y k 2 k 3 x Move cluster centers to mean of each cluster

K-means clustering (k=3) k 1 y k 2 k 3 x Reassign points to nearest cluster center

K-means clustering (k=3) k 1 y k 2 k 3 x Reassign points to nearest cluster center

K-means clustering (k=3) k 1 y k 2 k 3 x Repeat step 3 -4 until cluster centers converge (don’t/hardly move)

K-means • Works with numeric data only 1) Pick k random points: initial cluster centers 2) Assign every item to its nearest cluster center (e. g. using Euclidean distance) 3) Move each cluster center to the mean of its assigned items 4) Repeat steps 2, 3 until convergence (change in cluster assignments less than a threshold)

K-means clustering: another example http: //www. youtube. com/watch? feature=player_embedded&v=za. Kjh 2 N 8 j. N 4#!

Discussion • • Result can vary significantly depending on initial choice of centers Can get trapped in local minimum • Example: initial cluster centers instances • To increase chance of finding global optimum: restart with different random seeds

K-means clustering summary Advantages • Simple, understandable • Instances automatically assigned to clusters Disadvantages • Must pick number of clusters beforehand • All instances forced into a single cluster • Sensitive to outliers

K-means variations k-medoids – instead of mean, use medians of each cluster • Mean of 1, 3, 5, 7, 1009 is 205 • Median of 1, 3, 5, 7, 1009 is 5 • For large databases, use sampling •

How to choose k? g g g One important parameter k, but how to choose? • Domain dependent, we simply want k clusters Alternative: repeat for several values of k and choose the best Example: • cluster mammals properties • each value of k leads to a different clustering • use an MDL-based encoding for the data in clusters • each additional cluster introduces a penalty • optimal for k = 6

Clustering Evaluation g g g Manual inspection Benchmarking on existing labels Cluster quality measures • • distance measures high similarity within a cluster, low across clusters

Hierarchical Clustering

Hierarchical clustering g Hierarchical clustering represented in dendrogram • tree structure containing hierarchical clusters • individual clusters in leafs, union of child clusters in nodes

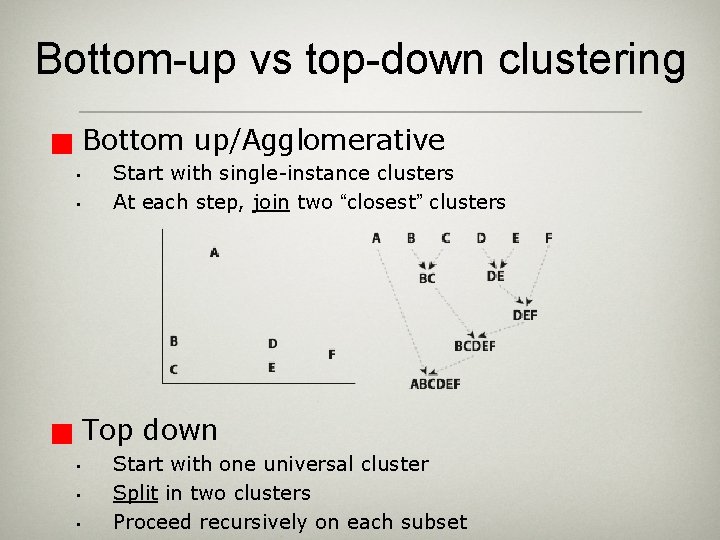
Bottom-up vs top-down clustering Bottom up/Agglomerative g • • Start with single-instance clusters At each step, join two “closest” clusters Top down g • • • Start with one universal cluster Split in two clusters Proceed recursively on each subset

Distance Between Clusters Centroid: distance between centroids • • Sometimes hard to compute (e. g. mean of molecules? ) • Single Link: smallest distance between points • Complete Link: largest distance between points • Average Link: average distance between points (d(A, C)+d(A, B)+d(B, C )+d(B, D))/4

How many clusters?

Probability-based Clustering Given k clusters, each instance belongs to all clusters (instead of a single one), with a certain probability • • mixture model: set of k distributions (one per cluster) • also: each cluster has prior likelihood • If correct clustering known, we know parameters and P(Ci) for each cluster: calculate P(Ci|x) using Bayes’ rule • How to estimate the unknown parameters?

Self-Organising Maps

Self Organizing Map Group similar data together g Dimensionality reduction g Data visualization technique g Similar to neural networks g Neurons try to mimic the input vectors g The winning neuron (and its neighborhood) wins g Topology preserving, using Neighborhood function g

Learning the SOM Determine the winner (the neuron of which the weight vector has the smallest distance to the input vector) g Move the weight vector w of the winning neuron towards the input i g i w Before learning i w After learning

SOM Learning Algorithm Initialise SOM (random, or such that dissimilar input is mapped far apart) g for t from 0 to N g Randomly select a training instance g Get the best matching neuron g calculate distance, e. g. g Scale neighbors g Who? decrease over time: Hexagons, squares, Gaussian, … g Update of neighbors towards the training instance g

Self Organizing Map Neighborhood function to preserve topological properties of the input space g Neighbors share the prize (postcode lottery principle) g

Self Organizing Map g g Input: high-dimension input space Output: low dimensional (typically 2 or 3) g g network topology Training Starting with a large learning rate and neighborhood size, both are gradually decreased to facilitate convergence g After learning, neurons with similar weights tend to cluster on the map g

SOM of hand-written numerals

SOM of countries (poverty)

Clustering Summary g g Unsupervised Many approaches • k-means – simple, sometimes useful • Hierarchical clustering – works for symbolic attributes • Self-Organizing Maps Evaluation is a problem • g k-medoids is less sensitive to outliers