Clustering in General n n In vector space

Clustering… in General n n In vector space, clusters are vectors found within e of a cluster vector, with different techniques for determining the cluster vector and e. Clustering is unsupervised pattern classification. n n Unsupervised means no correct answer or feedback. Patterns typically are samples of feature vectors or matrices. n Classification means collecting the samples into groups of similar members.

Clustering Decisions n Pattern Representation n Pattern proximity n n feature selection (e. g. , stop word removal, stemming) number of categories distance measure on pairs of patterns Grouping n characteristics of clusters (e. g. , fuzzy, hierarchical) Clustering algorithms embody different assumptions about these decisions and the form of clusters.

Formal Definitions n n n Feature vector x is a single datum of d measurements. Hard clustering techniques assign a class label to each cluster; members of clusters are mutually exclusive. Fuzzy clustering techniques assign a fractional degree of membership to each label for each x.

Proximity Measures n n Generally, use Euclidean distance or mean squared distance. In IR, use similarity measure from retrieval (e. g. , cosine measure for TFIDF).

[Jain, Murty & Flynn] Taxonomy of Clustering Hierarchical Single Link Complete Link HAC Partitional Square Error k-means Graph Theoretic Mixture Resolving Expectation Minimization Mode Seeking

Clustering Issues Agglomerative: begin with each sample in its own cluster and merge Hard: mutually exclusive cluster membership Divisive: begin with single cluster and split Fuzzy: degrees of membership in clusters Deterministic Stochastic Incremental: samples Batch: clusters created may be added to clusters over entire sample space

Hierarchical Algorithms n n n Produce hierarchy of classes (taxonomy) from singleton clusters to just one cluster. Select level for extracting cluster set. Representation is a dendrogram.

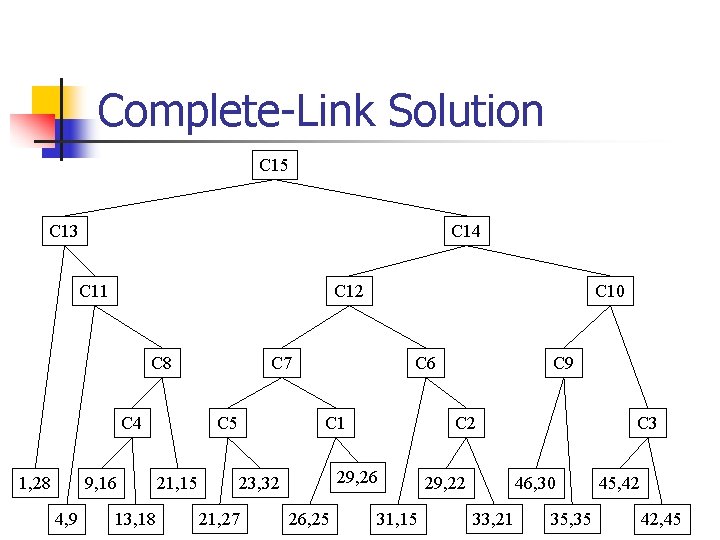
Complete-Link Revisited n n 1. 2. 3. 4. Used to create statistical thesaurus Agglomerative, hard, deterministic, batch Start with 1 cluster/sample Find two clusters with lowest distance Merge two clusters and add to hierarchy Repeat from 2 until termination criterion or until all clusters have merged

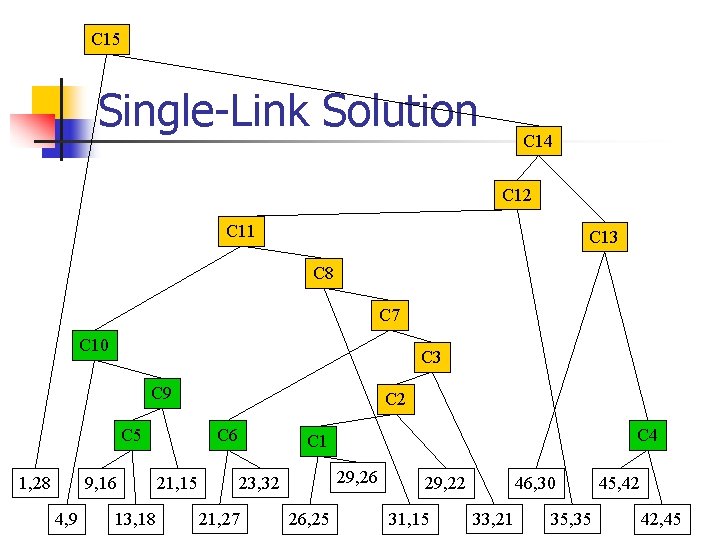
Single-Link n Like Complete-Link except… n n use minimum of distances between all pairs of samples in the two clusters (complete-link uses maximum). Single-link has chaining effect with elongated clusters, but can construct more complex shapes.

Example: Plot

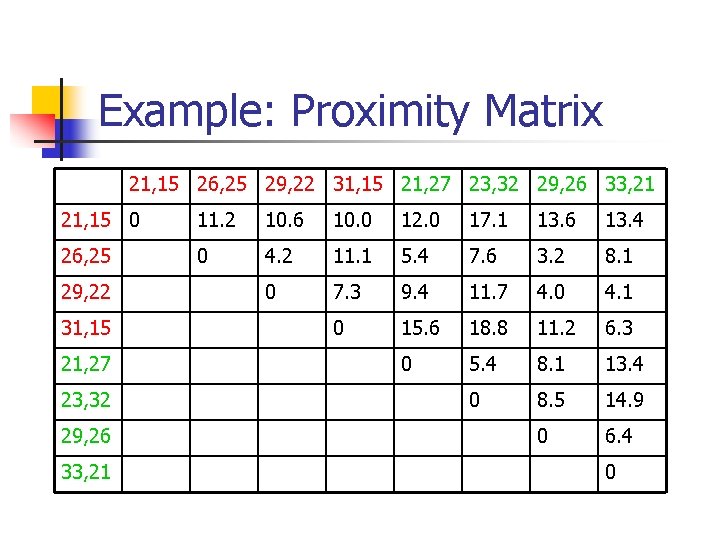
Example: Proximity Matrix 21, 15 26, 25 29, 22 31, 15 21, 27 23, 32 29, 26 33, 21 21, 15 0 11. 2 10. 6 10. 0 12. 0 17. 1 13. 6 13. 4 26, 25 0 4. 2 11. 1 5. 4 7. 6 3. 2 8. 1 0 7. 3 9. 4 11. 7 4. 0 4. 1 0 15. 6 18. 8 11. 2 6. 3 0 5. 4 8. 1 13. 4 0 8. 5 14. 9 0 6. 4 29, 22 31, 15 21, 27 23, 32 29, 26 33, 21 0

Complete-Link Solution C 15 C 13 C 14 C 11 C 12 C 8 C 4 1, 28 9, 16 4, 9 13, 18 C 7 C 5 21, 15 C 10 C 6 C 1 21, 27 C 2 29, 26 23, 32 26, 25 C 9 31, 15 C 3 46, 30 29, 22 33, 21 35, 35 45, 42 42, 45

C 15 Single-Link Solution C 14 C 12 C 11 C 13 C 8 C 7 C 10 C 3 C 9 C 5 1, 28 9, 16 4, 9 13, 18 C 2 C 6 21, 15 C 4 C 1 29, 26 23, 32 21, 27 26, 25 46, 30 29, 22 31, 15 33, 21 35, 35 45, 42 42, 45

Hierarchical Agglomerative Clustering (HAC) n 1. 2. 3. n n Agglomerative, hard, deterministic, batch Start with 1 cluster/sample and compute a proximity matrix between pairs of clusters. Merge most similar pair of clusters and update proximity matrix. Repeat 2 until all clusters merged. Difference is in how proximity matrix is updated. Ability to combine benefits of both single and complete link algorithms.

HAC for IR Intra-cluster Similarity Proximity is similarity of all documents to the cluster centroid. n Select pair of clusters that produces the smallest decrease in similarity, e. g. , if merge(X, Y)=>Z, then max[Sim(Z)-(Sim(X)+Sim(Y))] n where S is TFIDF vectors for documents, c is centroid of cluster X, and d is a document.

HAC for IR- Alternatives Centroid Similarity cosine similarity between the centroid of the two clusters UPGMA

Partitional Algorithms n n Results in set of unrelated clusters. Issues: n n n how many clusters is enough? how to search space of possible partitions? what is appropriate clustering criterion?

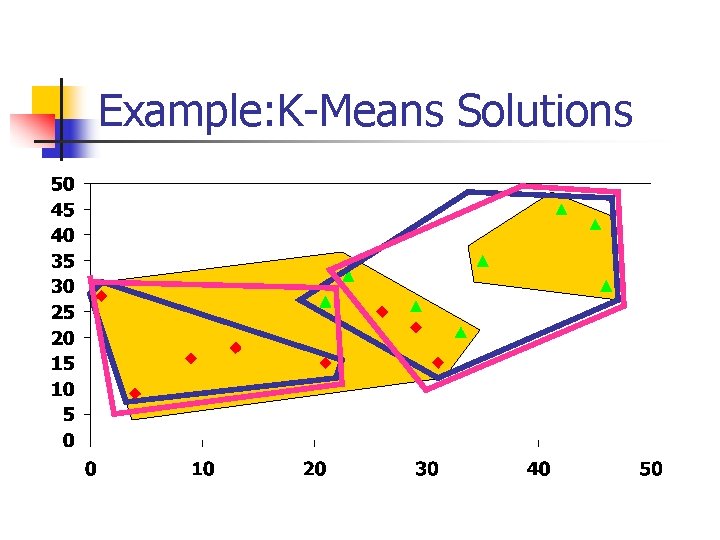
K Means n n n Number of clusters is set by user to be k. Non-deterministic Clustering criterion is squared error: where S is document set, L is a clustering, K is number of clusters, x is ith document in jth cluster and c is centroid of jth cluster.

k-Means Clustering Algorithm 1. 2. 3. 4. Randomly select k samples as cluster centroids. Assign each pattern to the closest cluster centroid. Recompute centroids. If convergence criterion (e. g. , minimal decrease in error or no change in cluster composition) is not met, return to 2.

Example: K-Means Solutions

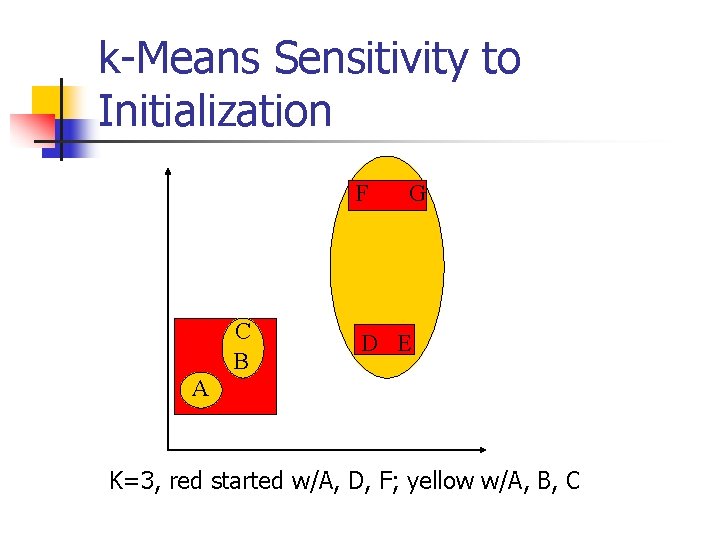
k-Means Sensitivity to Initialization F C B G D E A K=3, red started w/A, D, F; yellow w/A, B, C

k-Means for IR n n n Update centroids incrementally Calculate centroid as with hierarchical methods. Can refine into a divisive hierarchical method by starting with single cluster and splitting using k-means until forms k clusters with highest summed similarities. (bisecting k-means)

Other Types of Clustering Algorithms Graph Theoretic: construct minimal spanning tree and delete edges with largest lengths Expectation Minimization (EM): assume clusters are drawn from distributions, use maximum likelihood to estimate parameters of distributions. Nearest Neighbors: iteratively assign each sample to the cluster of its nearest labelled neighbor, so long as distance is below a set threshold.

Comparison of Clustering Algorithms [Steinbach et al. ] n n Implement 3 versions of HAC and 2 versions of k. Means Compare performance on documents hand labelled as relevant to one of a set of classes. Well known data sets (TREC) Found that UPGMA is best of hierarchical, but bisecting k-means seems to do better if considered over many runs. M. Steinbach, G. Karypis, V. Kumar. A Comparison of Document Clustering Techniques, KDD Workshop on Text Mining, 2000.

Evaluation Metrics 1 Evaluation: how to measure cluster quality? n Entropy: where pij is probability that a member of cluster j belongs to class i, nj is size of cluster j, m is number of clusters, n is number of docs and CS is a clustering solution.

Comparison Measure 2 n F measure: combines precision and recall n treat each cluster as the result of a query and each class as the relevant set of docs nij is # of members of class i in cluster j, nj is # in j, ni is # in i, n is # of docs.