Clustering 1 The KMeans Clustering Method l Example

Clustering 1

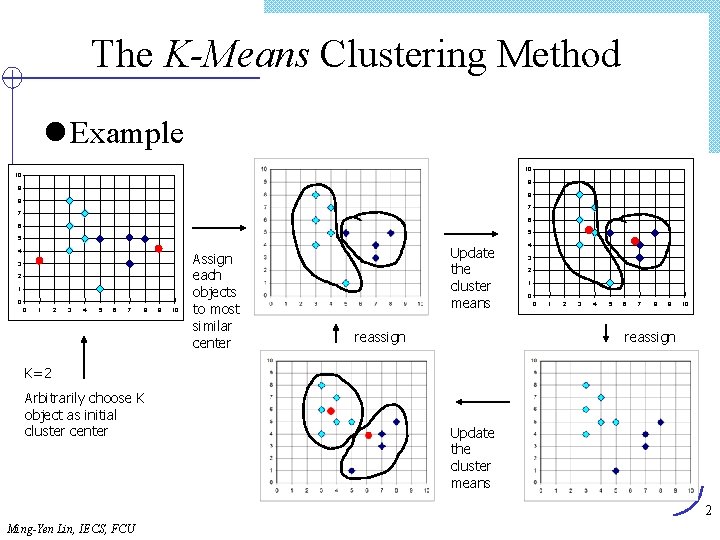
The K-Means Clustering Method l Example 10 10 9 9 8 8 7 7 6 6 5 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 Assign each objects to most similar center Update the cluster means reassign 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 reassign K=2 Arbitrarily choose K object as initial cluster center Update the cluster means 2 Ming-Yen Lin, IECS, FCU

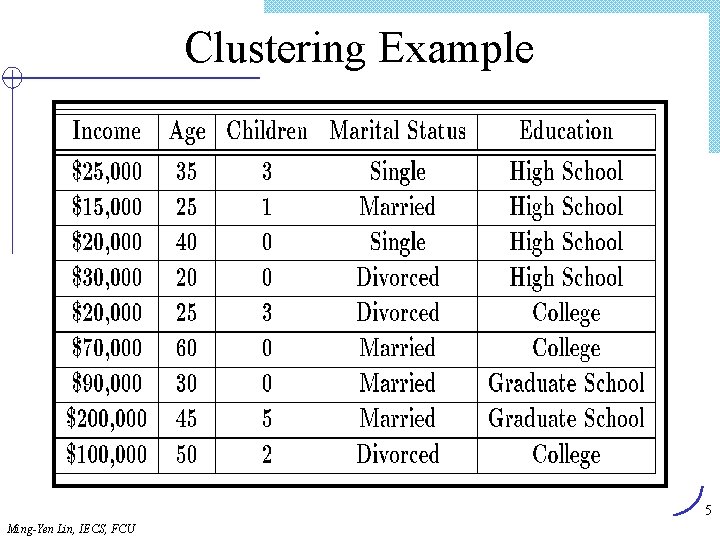
Cluster Analysis 群聚分析 l Cluster 群聚: 一群 data objects Ø 在同一群內相當相似 Ø 在不同群內非常不相似 l Cluster analysis Ø 把資料依相似性分群 l Clustering 是 unsupervised classification: 無預先設好 的類別標籤 l Typical applications Ø 作為了解資料分佈的 具(stand-alone tool) Ø 作為 其他方法的 preprocessing step 3 Ming-Yen Lin, IECS, FCU

Clustering Examples l Segment customer databased on similar buying patterns. Ø Marketing: Help marketers discover distinct groups in their customer bases, and then use this knowledge to develop targeted marketing programs l Group houses in a town into neighborhoods based on similar features. Ø City-planning: Identifying groups of houses according to their house type, value, and geographical location l Identify similar Web usage patterns Ø Document classification Ø Cluster Weblog data to discover groups of similar access patterns Ming-Yen Lin, IECS, FCU 4

Clustering Example 5 Ming-Yen Lin, IECS, FCU

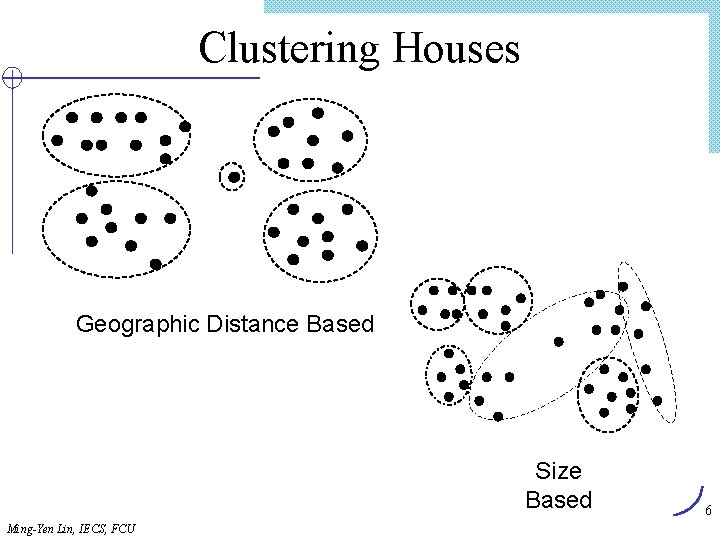
Clustering Houses Geographic Distance Based Size Based Ming-Yen Lin, IECS, FCU 6

何謂 Good Clustering? l 好的分群方法產生高品質的 clusters Ø high intra-class similarity （cluster 內：高相似） Ø low inter-class similarity （cluster 間：低相似） l 結果的品質決定於 clustering 方法的 Ø similarity measure Ø implementation l clustering 方法的品質也可以用「找出(部分或全部) 隱藏的 pattern 能力」來度量 7 Ming-Yen Lin, IECS, FCU

Clustering 需求 (Requirements/Issues) l 擴充性 （scalability ） l 處理各種型態的屬性 （types of attributes） l 找出任意形狀的cluster l 決定輸入參數時需盡量減少所需的 domain knowledge l 處理noise 及outlier的能力 l 對輸入資料的順序要 insensitive l high dimensionality l 可以整合 user-specified constraints l Interpretability l Usability l Dynamic data: if cluster membership changes over time 8 Ming-Yen Lin, IECS, FCU

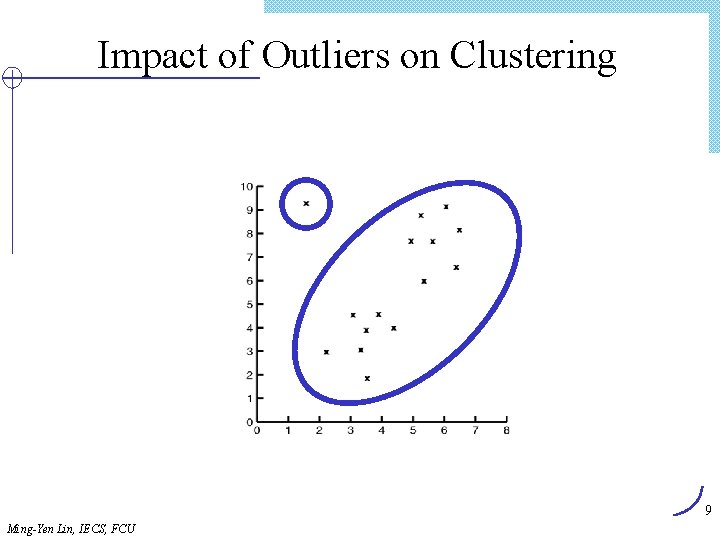
Impact of Outliers on Clustering 9 Ming-Yen Lin, IECS, FCU

資料結構 l Data matrix Ø(two modes) n obj. * p var. l Dissimilarity matrix Ø(one mode) n*n 10 Ming-Yen Lin, IECS, FCU

Clustering Quality 的度量 l Dissimilarity/Similarity metric: 以 distance function表 示，d(i, j) l Distance functions 的定義依照變數型態而不同 Ø interval-scaled, boolean, categorical, ordinal and ratio variables l 依照各個應用與資料的意義訂定變數的weights l 有時很難定義 “similar enough” or “good enough” Ø 答案很主觀 11 Ming-Yen Lin, IECS, FCU

Similarity and Dissimilarity Between Objects l Distances: 度量兩data objects的 similarity 或 dissimilarity Ø properties nd(i, j) 0 nd(i, i) = 0 nd(i, j) = d(j, i) nd(i, j) d(i, k) + d(k, j) l Manhattan distance l Euclidean distance 12 Ming-Yen Lin, IECS, FCU

Similarity and Dissimilarity (Cont. ) l Minkowski distance: i = (xi 1, xi 2, …, xip) and j = (xj 1, xj 2, …, xjp) 是兩個 pdimensional 的 data objects, q 是正整數 l Manhattan distance: q = 1 l Euclidean distance: q = 2 13 Ming-Yen Lin, IECS, FCU

Clustering Analysis 的資料型態 l Interval-scaled variables Ø weight, height, latitude, … (roughly linear) l Binary variables Ø symmetric: gender Ø asymmetric: fever (Y/N), test (P/N) l Nominal, ordinal, and ratio variables Ø map_color, weather; ordering; Ae. Bt l Variables of mixed types 14 Ming-Yen Lin, IECS, FCU

Interval-valued variables l Standardize data 先標準化 (xif 變成zif) Ø 算 mean absolute deviation where mf: 平均 Ø 算 standardized measurement (z-score) l 用 mean absolute deviation 比用 standard deviation 更 robust Ø standard deviation 對差值平方 15 Ming-Yen Lin, IECS, FCU

Binary Variables l A contingency table for binary data 各種可能 Object j Object i l Simple matching coefficient (invariant, if the binary variable is symmetric): l Jaccard coefficient (noninvariant if the binary variable is asymmetric): 16 Ming-Yen Lin, IECS, FCU

Dissimilarity between Binary Variables l Example Ø gender 是 symmetric attribute Ø 其他是 asymmetric binary attribute Ø 讓 Y 跟 P 為 1, N 為 0 17 Ming-Yen Lin, IECS, FCU

Nominal Variables l binary variable 的 generalization : 超過兩種狀態，如 red, yellow, blue, green l Method 1: Simple matching Ø m: # of matches, p: total # of variables l Method 2: use a large number of binary variables Ø creating a new binary variable for each of the M nominal states l Show an example 18 Ming-Yen Lin, IECS, FCU

Ordinal Variables l Can be discrete or continuous l Order is important, e. g. , rank l Can be treated like interval-scaled Ø 將 xif 用他的 rank替代, rif {1, …, Mf} Ø 將各個 ordinal variable 對應到 [0, 1] n 取代 i-th object 的 f-th 變數 Ø 用 interval-scaled variables的方法計算dissimilarity l Example 19 Ming-Yen Lin, IECS, FCU

Ratio-Scaled Variables l Ratio-scaled variable: a positive measurement on a nonlinear scale, approximately at exponential scale, such as Ae. Bt or Ae-Bt l Methods: Ø treat them like interval-scaled variables—not a good choice! (why? —the scale can be distorted) Ø apply logarithmic transformation, (log-log maybe) yif = log(xif) Ø treat them as continuous ordinal data n as ordinal data, treat their rank as interval-scaled 20 Ming-Yen Lin, IECS, FCU

Variables of Mixed Types l 資料庫可能同時包含這六種variables Ø symmetric binary, asymmetric binary, nominal, ordinal, interval and ratio l 可以用 weighted formula 來結合 ij(f) = 0: (1) 缺 xif 或 xjf (2) xif=xjf =0, f asymmetric 其他： ij(f) = 1 Ø 當 f 是 binary or nominal: dij(f) = 0 if xif = xjf , otherwise dij(f) = 1 Ø 當 f 是interval-based: dij(f) = |xif-xjf|/max(xf)-min(xf) Ø 當 f 是ordinal or ratio-scaled n算 ranks rif n把 zif 當 interval-scaled 21 Ming-Yen Lin, IECS, FCU

Types of Clustering l Hierarchical – Nested set of clusters created. l Partitional – One set of clusters created. l Incremental – Each element handled one at a time. l Simultaneous – All elements handled together. l Overlapping/Non-overlapping 22 Ming-Yen Lin, IECS, FCU

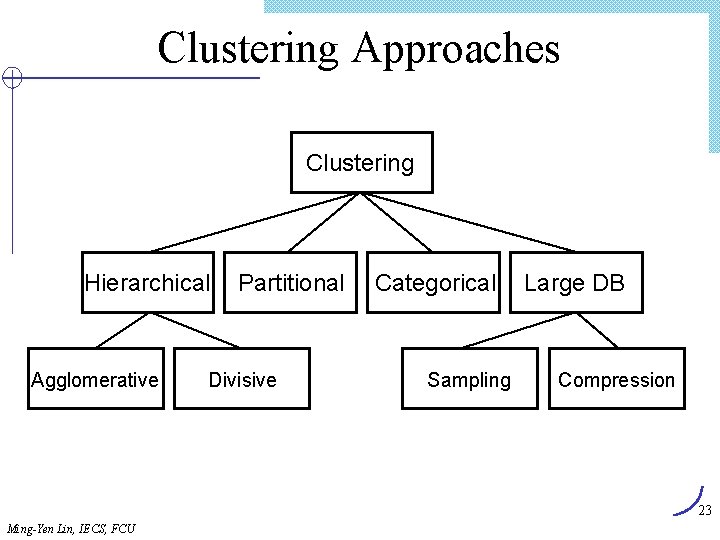
Clustering Approaches Clustering Hierarchical Agglomerative Partitional Divisive Categorical Sampling Large DB Compression 23 Ming-Yen Lin, IECS, FCU

Major Clustering Approaches l Partitioning algorithms Ø Construct various partitions Ø evaluate them by some criterion l Hierarchical algorithms Ø Create a hierarchical decomposition of the set of data (or objects) using some criterion l Density-based: based on connectivity and density functions l Grid-based: based on a multiple-level granularity structure l Model-based: A model is hypothesized for each of the clusters and the idea is to find the best fit of that model to each other 24 Ming-Yen Lin, IECS, FCU

Partitional Algorithms l K-Means l K-Nearest Neighbor l PAM l BEA l GA 25 Ming-Yen Lin, IECS, FCU

Partitioning Algorithms: Basic Concept l Partitioning method: Construct a partition of a database D of n objects into a set of k clusters l Given a k, find a partition of k clusters that optimizes the chosen partitioning criterion Ø Global optimal: exhaustively enumerate all partitions Ø Heuristic methods: k-means and k-medoids algorithms Ø k-means (Mac. Queen’ 67): Each cluster is represented by the center of the cluster Ø k-medoids or PAM (Partition around medoids) (Kaufman & Rousseeuw’ 87): Each cluster is represented by one of the objects in the cluster 26 Ming-Yen Lin, IECS, FCU

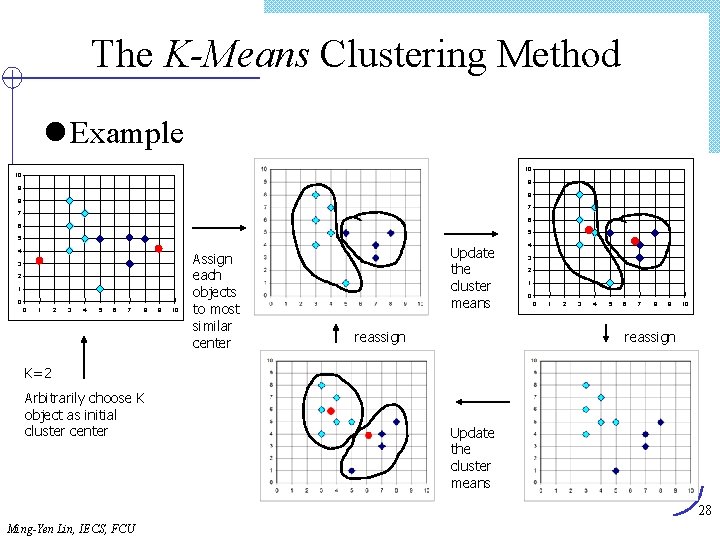
The K-Means Clustering Method l Given k, the k-means algorithm is implemented in four steps: Ø Partition objects into k nonempty subsets Ø Compute seed points as the centroids of the clusters of the current partition (the centroid is the center, i. e. , mean point, of the cluster) Ø Assign each object to the cluster with the nearest seed point Ø Go back to Step 2, stop when no more new assignment lcluster mean is mi = (1/m)(ti 1 + … + tim) 27 Ming-Yen Lin, IECS, FCU

The K-Means Clustering Method l Example 10 10 9 9 8 8 7 7 6 6 5 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 Assign each objects to most similar center Update the cluster means reassign 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 reassign K=2 Arbitrarily choose K object as initial cluster center Update the cluster means 28 Ming-Yen Lin, IECS, FCU

K-Means Example l Given: {2, 4, 10, 12, 3, 20, 30, 11, 25}, k=2 l Randomly assign means: m 1=3, m 2=4 l K 1={2, 3}, K 2={4, 10, 12, 20, 30, 11, 25}, m 1=2. 5, m 2=16 l K 1={2, 3, 4}, K 2={10, 12, 20, 30, 11, 25}, m 1=3, m 2=18 l K 1={2, 3, 4, 10}, K 2={12, 20, 30, 11, 25}, m 1=4. 75, m 2=19. 6 l K 1={2, 3, 4, 10, 11, 12}, K 2={20, 30, 25}, m 1=7, m 2=25 l Stop as the clusters with these means are the same. 29 Ming-Yen Lin, IECS, FCU

Comments on the K-Means Method l Strength: Relatively efficient: O(tkn), where n is # objects, k is # clusters, and t is # iterations. Normally, k, t << n. n Comparing: PAM: O(k(n-k)2 ), CLARA: O(ks 2 + k(n-k)) l Comment: Often terminates at a local optimum. l Weakness Ø Applicable only when mean is defined, then what about categorical data? Ø Need to specify k, the number of clusters, in advance Ø Unable to handle noisy data and outliers Ø Not suitable to discover clusters with non-convex shapes 30 Ming-Yen Lin, IECS, FCU

K-Means 的問題 l The k-means algorithm is sensitive to outliers ! Ø Since an object with an extremely large value may substantially distort the distribution of the data. l K-Medoids: Instead of taking the mean value of the object in a cluster as a reference point, medoids can be used, which is the most centrally located object in a cluster. 10 10 9 9 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 0 0 0 1 2 Ming-Yen Lin, IECS, FCU 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 PAM (Partitioning Around Medoids, 1987) 31

K-Nearest Neighbor l Items are iteratively merged into the existing clusters that are closest. l Incremental l Threshold, t, used to determine if items are added to existing clusters or a new cluster is created. 32 Ming-Yen Lin, IECS, FCU

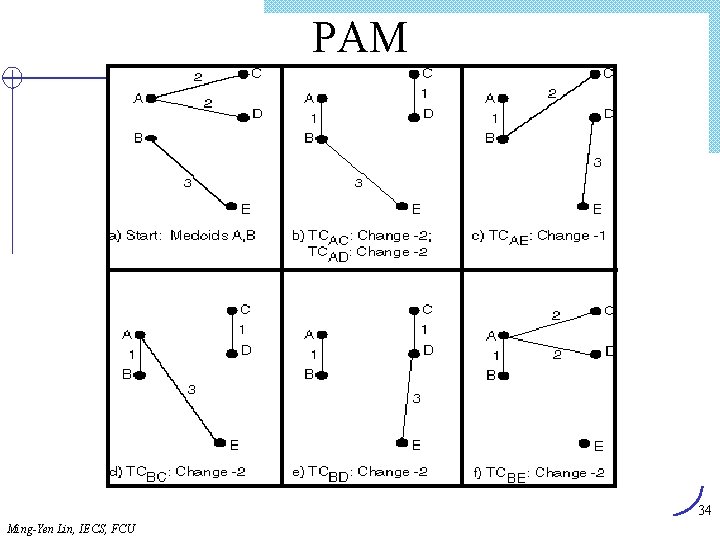
PAM l Partitioning Around Medoids (PAM) (KMedoids) l Handles outliers well. l Ordering of input does not impact results. l Does not scale well. l Each cluster represented by one item, called the medoid. l Initial set of k medoids randomly chosen. 33 Ming-Yen Lin, IECS, FCU

PAM 34 Ming-Yen Lin, IECS, FCU

PAM Cost Calculation l At each step in algorithm, medoids are changed if the overall cost is improved. l Cjih – cost change for an item tj associated with swapping medoid ti with non-medoid th. 35 Ming-Yen Lin, IECS, FCU

BEA l l Bond Energy Algorithm Database design (physical and logical) Vertical fragmentation Determine affinity (bond) between attributes based on common usage. l Algorithm outline: 1. Create affinity matrix 2. Convert to BOND matrix 3. Create regions of close bonding 36 Ming-Yen Lin, IECS, FCU

BEA Modified from [OV 99] 37 Ming-Yen Lin, IECS, FCU

Genetic Algorithm Example l {A, B, C, D, E, F, G, H} l Randomly choose initial solution: {A, C, E} {B, F} {D, G, H} or 10101000, 0100, 00010011 l Suppose crossover at point four and choose 1 st and 3 rd individuals: 10100011, 0100, 00011000 l What should termination criteria be? 38 Ming-Yen Lin, IECS, FCU

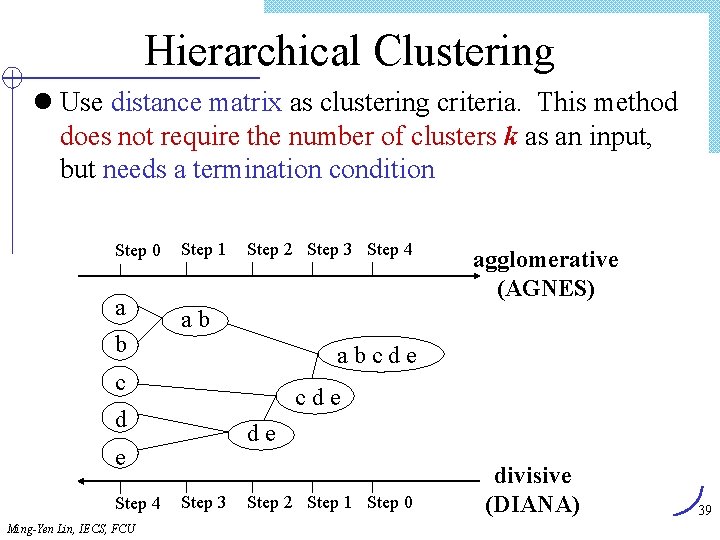
Hierarchical Clustering l Use distance matrix as clustering criteria. This method does not require the number of clusters k as an input, but needs a termination condition Step 0 a b Step 1 Step 2 Step 3 Step 4 ab abcde c cde d de e Step 4 Ming-Yen Lin, IECS, FCU agglomerative (AGNES) Step 3 Step 2 Step 1 Step 0 divisive (DIANA) 39

AGNES (Agglomerative Nesting) l Implemented in Splus (e. g) l Use Single-Linkage method and the dissimilarity matrix l Merge nodes that have the least dissimilarity l Go on in a non-descending fashion l Eventually all nodes belong to the same cluster Single-linkage: cloest pair Complete-linkage: distant 40 Ming-Yen Lin, IECS, FCU

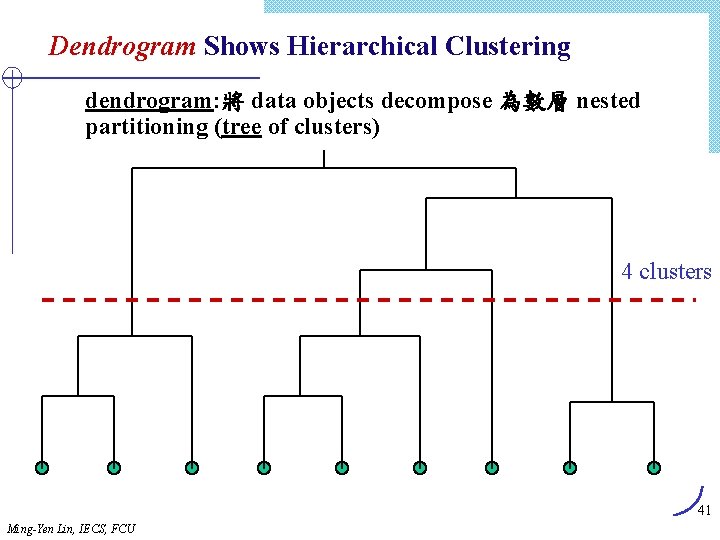
Dendrogram Shows Hierarchical Clustering dendrogram: 將 data objects decompose 為數層 nested partitioning (tree of clusters) 4 clusters 41 Ming-Yen Lin, IECS, FCU

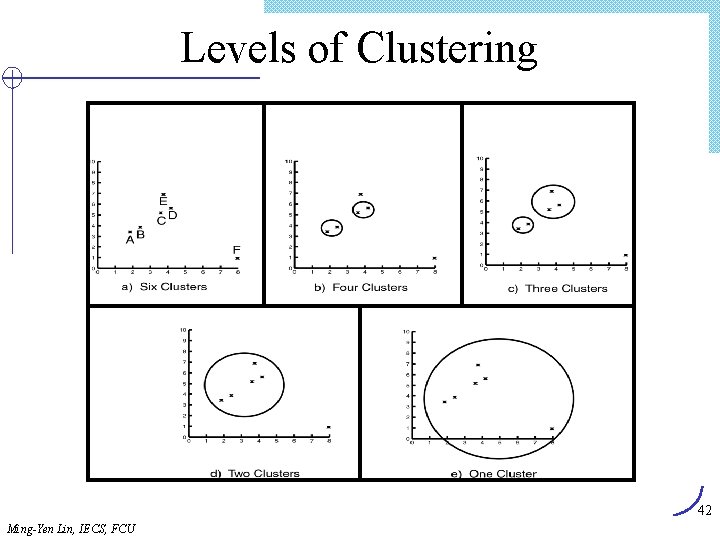
Levels of Clustering 42 Ming-Yen Lin, IECS, FCU

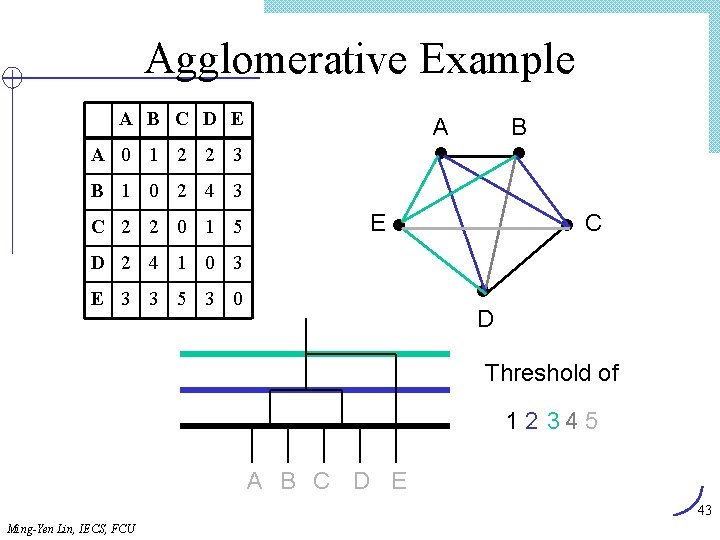
Agglomerative Example A B C D E A B A 0 1 2 2 3 B 1 0 2 4 3 C 2 2 0 1 5 E C D 2 4 1 0 3 E 3 3 5 3 0 D Threshold of 1 2 34 5 A B C D E 43 Ming-Yen Lin, IECS, FCU

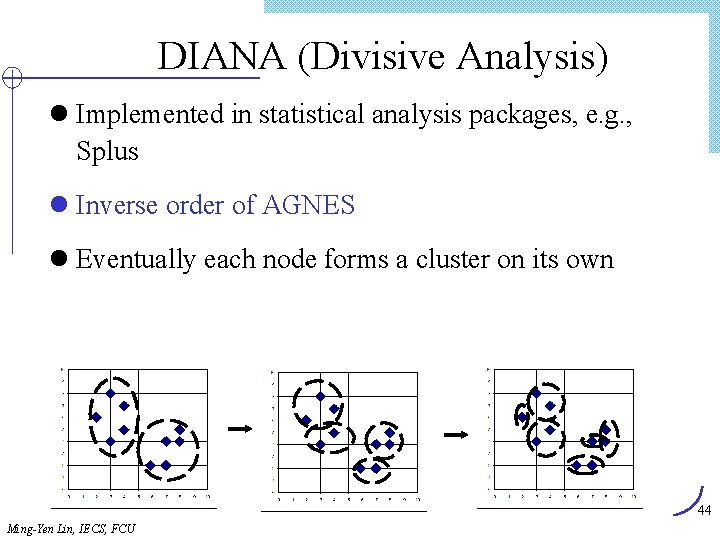
DIANA (Divisive Analysis) l Implemented in statistical analysis packages, e. g. , Splus l Inverse order of AGNES l Eventually each node forms a cluster on its own 44 Ming-Yen Lin, IECS, FCU

Distance Between Clusters l Single Link: smallest distance between points l Complete Link: largest distance between points l Average Link: average distance between points l Centroid: distance between centroids 45 Ming-Yen Lin, IECS, FCU

Density-Based Clustering Methods l Clustering based on density (local cluster criterion), such as density-connected points l Major features: Ø Ø Discover clusters of arbitrary shape Handle noise One scan Need density parameters as termination condition l Several interesting studies: Ø Ø DBSCAN: Ester, et al. (KDD’ 96) OPTICS: Ankerst, et al (SIGMOD’ 99). DENCLUE: Hinneburg & D. Keim (KDD’ 98) CLIQUE: Agrawal, et al. (SIGMOD’ 98) 46 Ming-Yen Lin, IECS, FCU

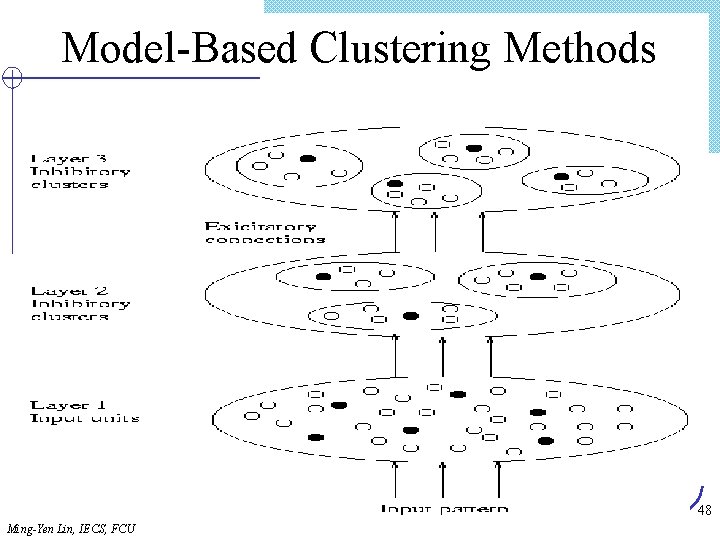
Model-Based Clustering Methods l Attempt to optimize the fit between the data and some mathematical model l Statistical approach Ø Conceptual clustering Ø COBWEB (Fisher’ 87) l AI approach Ø a “prototype” for each cluster (called exemplar) Ø put new obj. to the most similar exemplar Ø Neural network approach n Self-Organization feature Map (SOM) – several units competing for the current object 47 Ming-Yen Lin, IECS, FCU

Model-Based Clustering Methods 48 Ming-Yen Lin, IECS, FCU

Self-organizing feature maps (SOMs) l Clustering is also performed by having several units competing for the current object l The unit whose weight vector is closest to the current object wins l The winner and its neighbors learn by having their weights adjusted l Useful for visualizing high-dimensional data in 2 - or 3 D space Example Tool 49 Ming-Yen Lin, IECS, FCU

What Is Outlier Discovery? l 何謂 outliers? Ø Michael Jordon、CEO薪水、age = 999 Ø 那些跟其他資料相當不相似的資料 (considerably dissimilar!) l Problem: find top k outliers among n objects l Applications: Ø Credit card/ Telecom fraud detection Ø Customer segmentation Ø Medical analysis l Approaches Ø Statistical-based Ø Distance-based Ø Deviation-based Ming-Yen Lin, IECS, FCU 50

Outlier Discovery: Statistical Approaches f Assume a model underlying distribution that generates data set (e. g. normal distribution) l Use discordancy tests depending on Ø data distribution Ø distribution parameter (e. g. , mean, variance) Ø number of expected outliers l Drawbacks Ø most tests are for single attribute Ø In many cases, data distribution may not be known 51 Ming-Yen Lin, IECS, FCU

Distance-Based Approach l 參數： p （為一分數）, D l Distance-based outlier DB(p, D)-outlier: dataset S中的 object O， S中至少 p 的object 跟 O 的距離大於 D Ø 沒有夠多的鄰居 l distance-based outlier mining algorithms Ø Index-based algorithm Ø Nested-loop algorithm Ø Cell-based algorithm l. . . Ming-Yen Lin, IECS, FCU

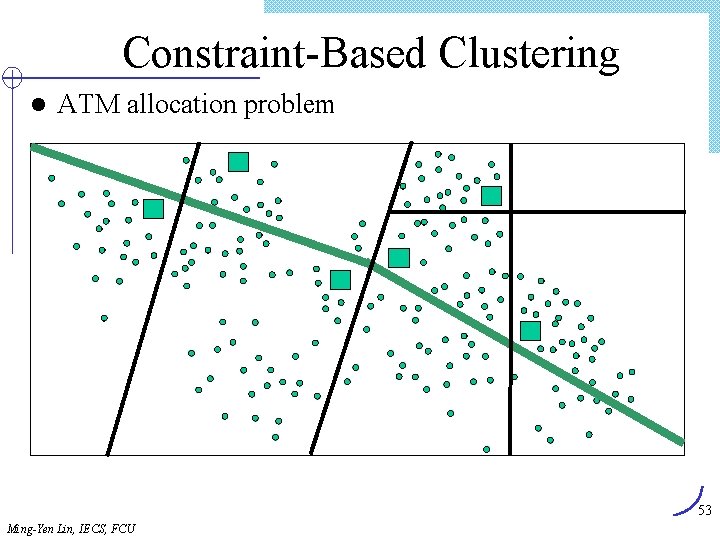
Constraint-Based Clustering l ATM allocation problem 53 Ming-Yen Lin, IECS, FCU

Clustering Large Databases l Most clustering algorithms assume a large data structure which is memory resident. l Clustering may be performed first on a sample of the database then applied to the entire database. l Algorithms Ø BIRCH Ø DBSCAN Ø CURE 54 Ming-Yen Lin, IECS, FCU

Desired Features for Large Databases l One scan (or less) of DB l Online l Suspendable, stoppable, resumable l Incremental l Work with limited main memory l Different techniques to scan (e. g. sampling) l Process each tuple once 55 Ming-Yen Lin, IECS, FCU

BIRCH l Balanced Iterative Reducing and Clustering using Hierarchies l Incremental, hierarchical, one scan l Save clustering information in a tree l Each entry in the tree contains information about one cluster l New nodes inserted in closest entry in tree 56 Ming-Yen Lin, IECS, FCU

Clustering Feature l CT Triple: (N, LS, SS) Ø N: Number of points in cluster Ø LS: Sum of points in the cluster Ø SS: Sum of squares of points in the cluster l CF Tree Ø Balanced search tree Ø Node has CF triple for each child Ø Leaf node represents cluster and has CF value for each subcluster in it. Ø Subcluster has maximum diameter 57 Ming-Yen Lin, IECS, FCU

BIRCH Algorithm 58 Ming-Yen Lin, IECS, FCU

Improve Clusters 59 Ming-Yen Lin, IECS, FCU

DBSCAN l Density Based Spatial Clustering of Applications with Noise l Outliers will not effect creation of cluster. l Input ØMin. Pts – minimum number of points in cluster ØEps – for each point in cluster there must be another point in it less than this distance away. 60 Ming-Yen Lin, IECS, FCU

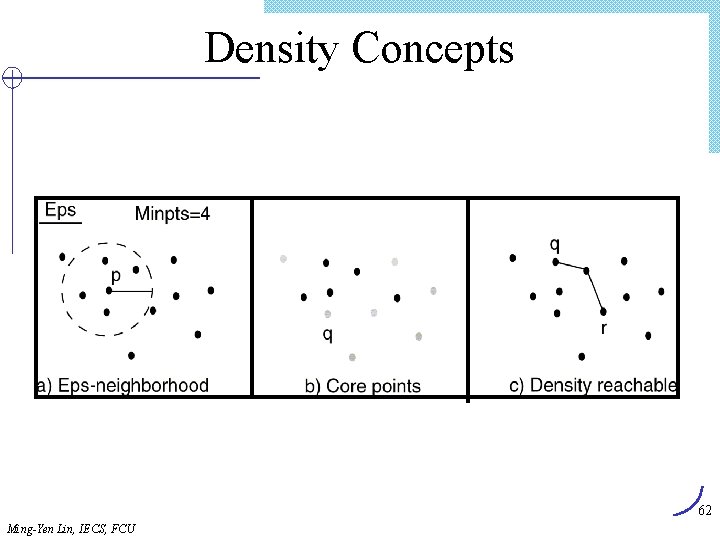
DBSCAN Density Concepts l Eps-neighborhood: Points within Eps distance of a point. l Core point: Eps-neighborhood dense enough (Min. Pts) l Directly density-reachable: A point p is directly density-reachable from a point q if the distance is small (Eps) and q is a core point. l Density-reachable: A point si density-reachable form another point if there is a path from one to the other consisting of only core points. 61 Ming-Yen Lin, IECS, FCU

Density Concepts 62 Ming-Yen Lin, IECS, FCU

DBSCAN Algorithm 63 Ming-Yen Lin, IECS, FCU

CURE l Clustering Using Representatives l Use many points to represent a cluster instead of only one l Points will be well scattered 64 Ming-Yen Lin, IECS, FCU

CURE Approach 65 Ming-Yen Lin, IECS, FCU

CURE Algorithm 66 Ming-Yen Lin, IECS, FCU

CURE for Large Databases 67 Ming-Yen Lin, IECS, FCU

Summary l Cluster analysis groups objects based on their similarity Ø cluster analysis has wide applications l Measure of similarity can be computed for various types of data l Clustering algorithms can be categorized into Ø Ø Ø partitioning methods hierarchical methods density-based methods grid-based methods model-based methods l Outlier detection and analysis Ø useful for fraud detection, etc. Ø performed by statistical, distance-based or deviation-based approaches l research issues: constraint-based clustering 68 Ming-Yen Lin, IECS, FCU

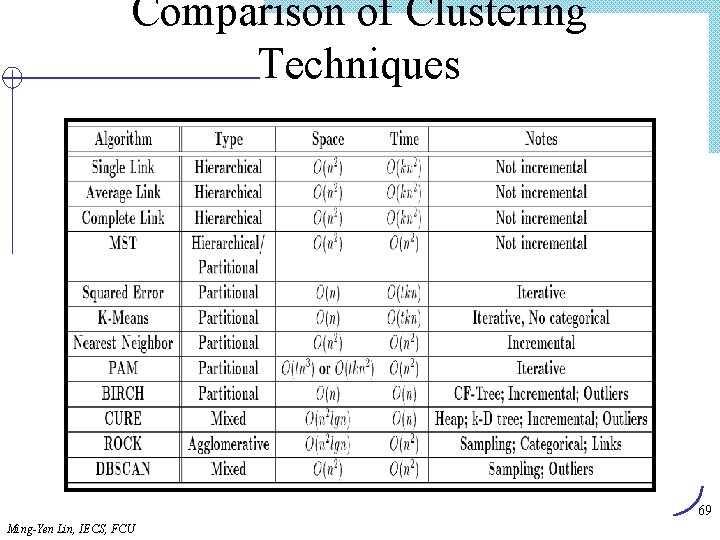
Comparison of Clustering Techniques 69 Ming-Yen Lin, IECS, FCU

Clustering vs. Classification l No prior knowledge ØNumber of clusters ØMeaning of clusters l Unsupervised learning l clusters are not known a priori! 70 Ming-Yen Lin, IECS, FCU