Cluster validation Integration ICES Bioinformatics Overview INTRODUCTION MICROARRAY

Cluster validation Integration ICES Bioinformatics

Overview INTRODUCTION MICROARRAY ANALYSIS VALIDATION OF THE RESULTS • Statistical validation • Biological validation INTEGRATION

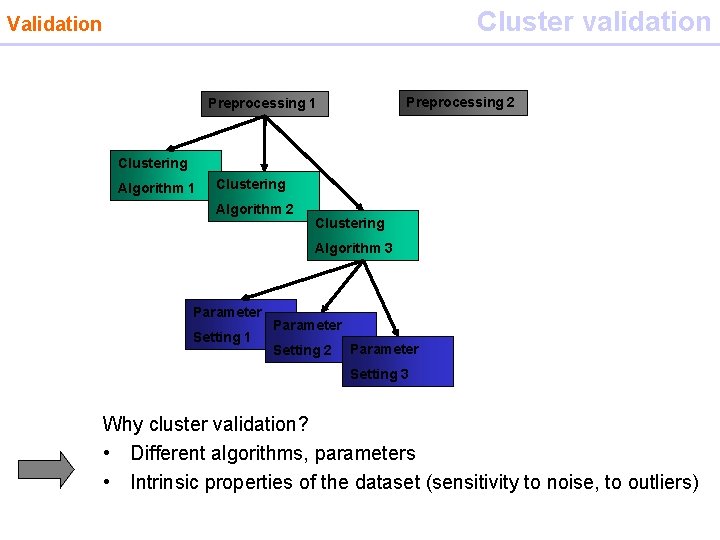
Cluster validation Validation Preprocessing 2 Preprocessing 1 Clustering Algorithm 2 Clustering Algorithm 3 Parameter Setting 1 Parameter Setting 2 Parameter Setting 3 Why cluster validation? • Different algorithms, parameters • Intrinsic properties of the dataset (sensitivity to noise, to outliers)

Statistical validation Validation STATISTICAL VALIDATION • Sensitivity analysis – Leaf one out cross validation (FOM) – Sensitivity analysis • Gaussian noise • ANOVA • Cluster coherence testing – Euclidean distance score – Gap statistics

Validation Statistical validation Figure of Merit (sensitivity towards an experiment) • Tested cluster algorithm is applied to all experimental conditions except the left out condition • Hypothesis: if the cluster algorithm is robust it can predict the measured values of the left out condition • To estimate the predictive power of the algorithm FOM is calculated This is repeated for all conditions and the average FOM is calculated FOM is the root mean square deviation in the left-out condition e of the individual gene expression levels relative to their cluster means Yeung et al. , 2001

Validation Statistical validation Sensitivity analysis towards the signal to noise ratio Sensitivity analysis = A way of assigning confidence to the cluster membership – create new in silico replica's of the dataset of interest by adding a small amount of noise on the original data – treat new datasets as the original one and cluster – Genes consistently clustered together over all in silico replicas are considered as robust towards adding noise How to determine the noise?

Statistical validation Validation How to determine the noise? How to generate simulated datasets? • Gaussian noise with m 0 and standard deviation s estimated as the median standard deviation for the log-ratios for all genes across the different experiment Bittner et al. 2000 • noise based on the appropriate ANOVA model • e describes the noise term • The values are the estimates from the original fit • The e are drawn with replacement from the studentized residuals of the original fit Clustering is repeated on the simulated datasets

Statistical validation Validation Comparing cluster results Approximate the confidence in the clustering output of a gene • cluster label known: determine the stability of a gene: the percent of bootstrap cluster experiments in which the gene matches to the same cluster Cluster exp 1 Cluster exp 2 C 1 Cluster exp 3 C 1 Cluster exp 4 C 1 • cluster label unknown: • Identify pairs of genes that cluster together in C^ and count the frequency with which such pairs cluster together in the bootstrapped clusters C^*. When each pair of genes clusters together reliably stable clusters will emerge • RAND INDEX (Yeung et al. 2001) • Jaccard coefficient (Ben-Hur et al. 2002) Cluster exp 1 C 2 C 3 … Cluster exp 2 C 1 C 2 C 3 … Cluster exp 3 C 1 C 2 C 3 … Cluster exp 4 C 1 C 2 C 3 …

Validation Statistical validation RAND index • statistic designed to assess the degree of agreement between two partitions • Usually an unknown partition against an external standard Adjusted RAND index • adjusted so that the expected value of the RAND index between two random partions is zero The rand index is defined as the fraction of agreement that is the number of pairs of objects that are either in same groups in both partitions (a) or in different groups in both partitions (b) divided by the total number of pairs of objects (a + b + c +d). The rand index lies between 0 and 1. a: the number of object pairs that are clustered together in data set 1 and in dataset 2 b: the number of object pairs that are clustered together in data set 1 but not in dataset 2 c: the number of object pairs that are clustered together in data set 2 but not in dataset 1 d: the number of object pairs that are put in different clusters in both datasets a, d: agreement between cluster results b, c: disagreement between cluster results

Statistical validation • Jaccard coefficient Based on the clusters of one dataset, binary pair vectors are calculated, where each element corresponds to a unique pair of genes and had a value one if both genes were clustered into the same cluster and zero otherwise. From two such pairvectors, where one was derived from the first dataset and the other from the second dataset, the jaccard coefficient is computed. This coefficient compares the correlation between both obtained binary matrices. Jaccard coefficient

Statistical validation Validation Cluster coherence testing Euclidian distance k points (genes) in cluster p experiments (dimensions) average profile of cluster j Vw: • Variance of the genes about the cluster averaged over all experiments • Maximizes coherence of the genes within a cluster

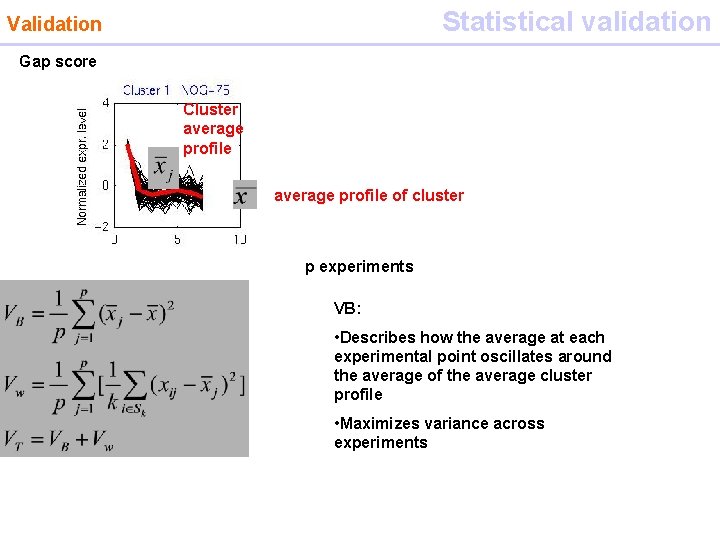
Statistical validation Validation Gap score Cluster average profile of cluster p experiments VB: • Describes how the average at each experimental point oscillates around the average of the average cluster profile • Maximizes variance across experiments

Validation Statistical validation Gap statistics Score function: • R 2 select clusters containing tightly co-expressed genes (minimal Vw) showing a high variable profile (high VB) across the experiments (ie affected by the signal studied). • Score is compared to a similar score calculated based on a randomly generated cluster (bootstrapping) • The difference between the score of the randomly generated cluster and the cluster of interest is calculated. (gapstatistics)

Overview INTRODUCTION MICROARRAY ANALYSIS VALIDATION OF THE RESULTS • Statistical validation • Biological validation INTEGRATION

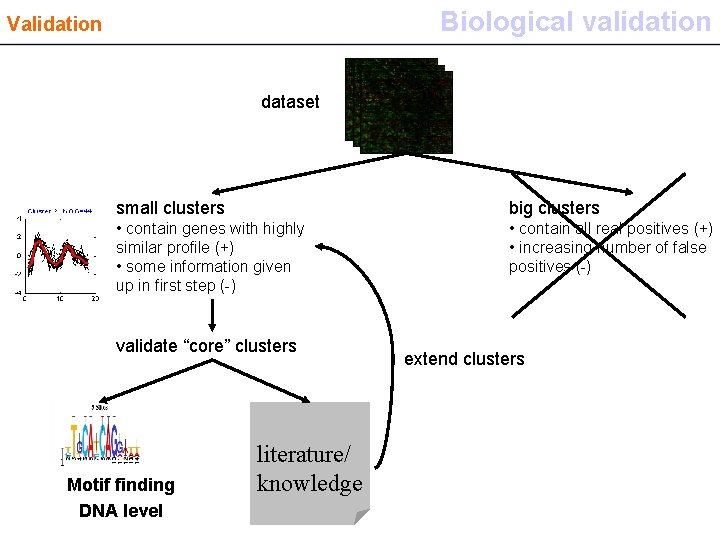
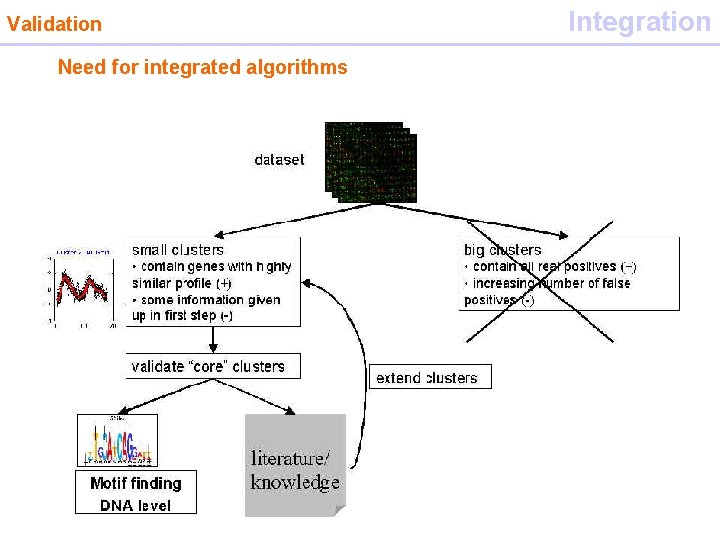
Biological validation Validation dataset small clusters big clusters • contain genes with highly similar profile (+) • some information given up in first step (-) • contain all real positives (+) • increasing number of false positives (-) validate “core” clusters Motif finding DNA level literature/ knowledge extend clusters

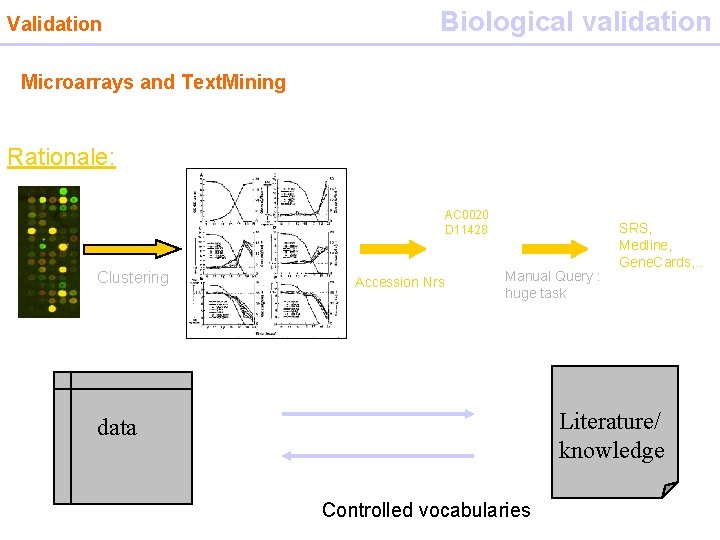
Validation Biological validation Microarrays and Text. Mining Rationale: AC 0020 D 11428 Clustering Accession Nrs Manual Query : huge task SRS, Medline, Gene. Cards, . . Literature/ knowledge data Controlled vocabularies

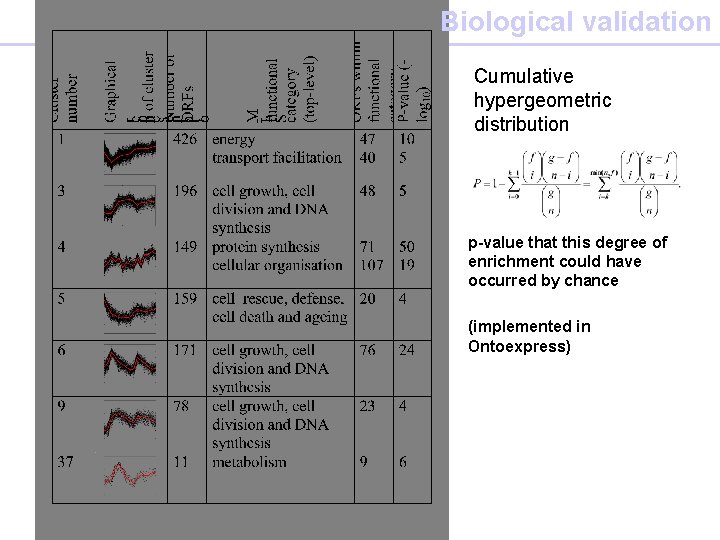
Biological validation Cumulative hypergeometric distribution p-value that this degree of enrichment could have occurred by chance (implemented in Ontoexpress)

Biological validation c 2 test or Fisher exact test (as implemented in FATIGO software) N 1: number of genes on the chip N 2: number of differentially expressed genes

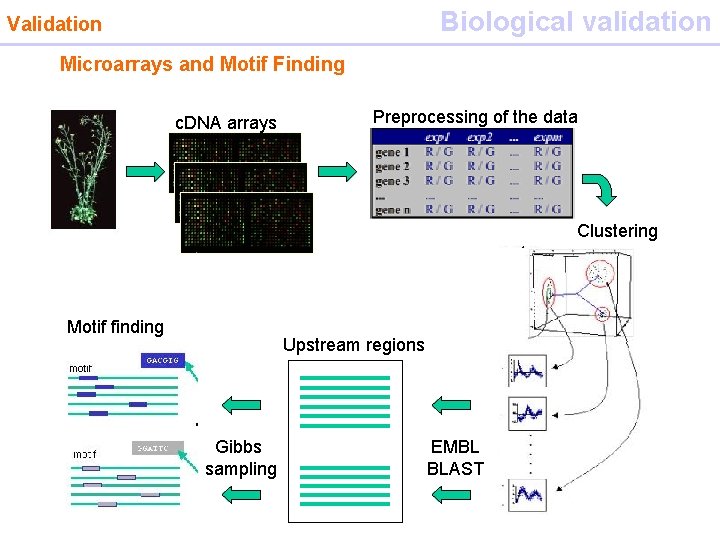
Biological validation Validation Microarrays and Motif Finding c. DNA arrays Preprocessing of the data Clustering Motif finding Upstream regions Gibbs sampling EMBL BLAST

Overview INTRODUCTION MICROARRAY ANALYSIS VALIDATION OF THE RESULTS • Statistical validation • Biological validation INTEGRATION • IT level • Algorithmic level

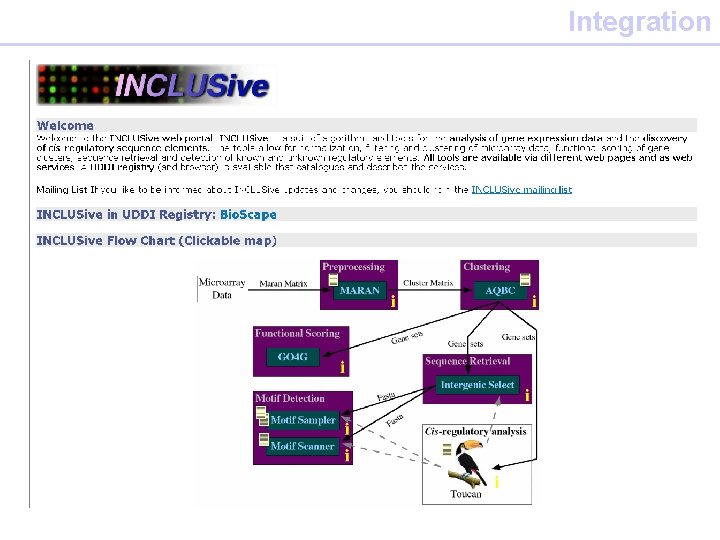
Integration

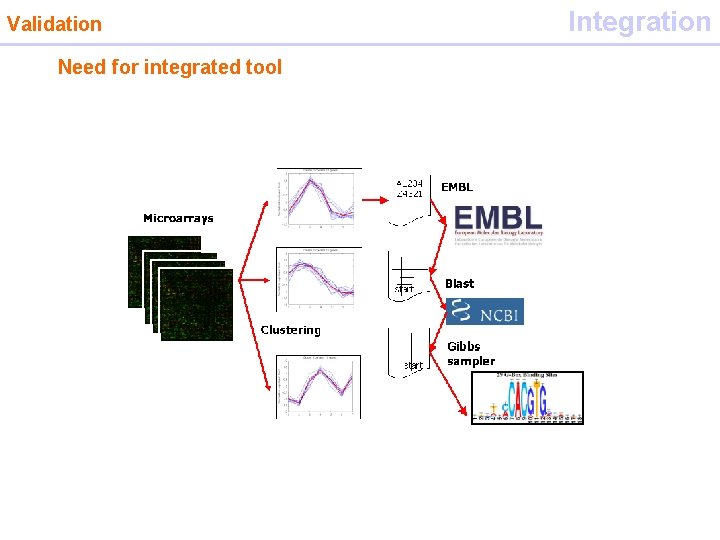
Validation Need for integrated tool Integration

Overview INTRODUCTION MICROARRAY ANALYSIS VALIDATION OF THE RESULTS • Statistical validation • Biological validation INTEGRATION • IT level • Algorithmic level

Validation Need for integrated algorithms Integration

Validation Integration • Retain high sensitivity (minimize number of false negatives) • Reduce level of noise (minimize number of false positives) • In corporate a priori information • Combine data from different sources that can mutually confirm each other • Example: sequence information and expression profiles • Server r. Motif (Lapidot and Pilpel, 2003) • Selects genes from a microarray if – Contain a motif – Have a highly correlated expression profile

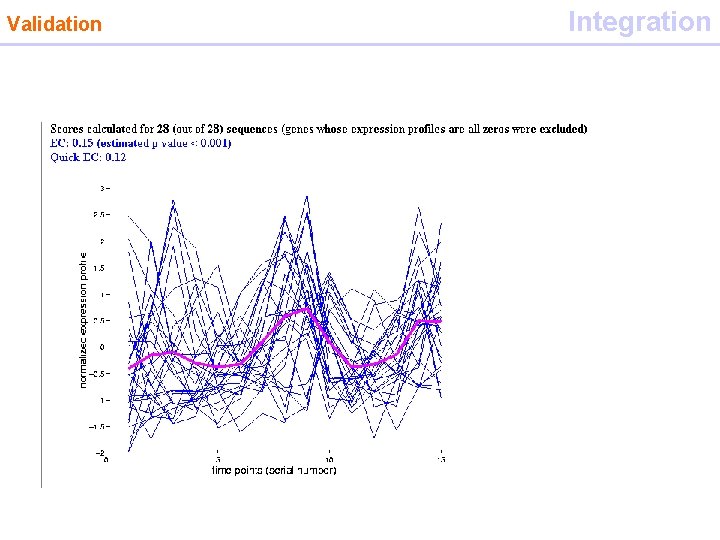
Validation Integration • Motif diagnosis tool • measures the extent to which a set of genes that contain a given motif in their promoter) display expression profiles similar to each other at a given set of conditions (analyzed by microarrays) • score (EC expression coherence) of a set of N genes is defined as the number of p pairs of genes in the set for which the Euclidean distance between the mean and variance normalized profiles falls below a threshold D, divided by the total number of pairs in the set • EC= p/[(0. 5(N)(N-1)]

Validation Integration