Cluster Validation Cluster validation q Assess the quality

Cluster Validation ¢ Cluster validation q Assess the quality and reliability of clustering results. ¢ Why validation? q. To avoid finding clusters formed by chance q. To compare clustering algorithms q. To choose clustering parameters m e. g. , the number of clusters in the K-means algorithm University at Buffalo The State University of New York

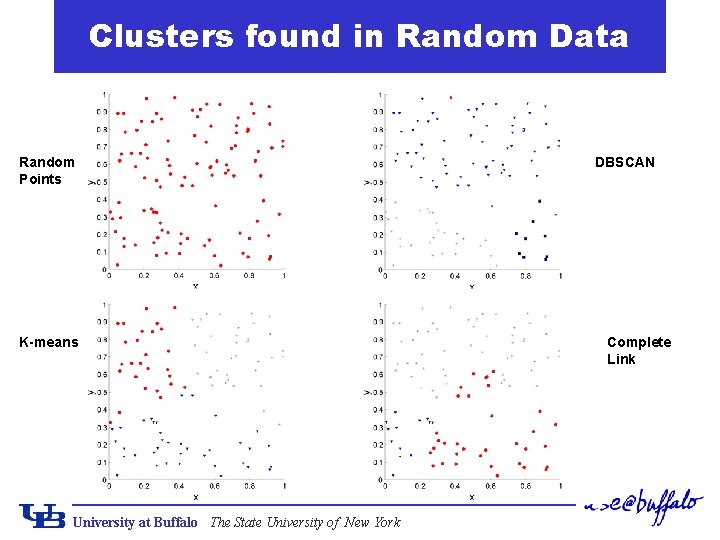
Clusters found in Random Data Random Points K-means University at Buffalo The State University of New York DBSCAN Complete Link

Aspects of Cluster Validation ¢ Comparing the clustering results to ground truth (externally known results). q External Index ¢ Evaluating the quality of clusters without reference to external information. q Use only the data q Internal Index ¢ Determining the reliability of clusters. q To what confidence level, the clusters are not formed by chance q Statistical framework University at Buffalo The State University of New York

Comparing to Ground Truth ¢ Notation q N: number of objects in the data set; q P={P 1, …, Pm}: the set of “ground truth” clusters; q C={C 1, …, Cn}: the set of clusters reported by a clustering algorithm. ¢ The “incidence matrix” q N N (both rows and columns correspond to objects). q Pij = 1 if Oi and Oj belong to the same “ground truth” cluster in P; Pij=0 otherwise. q Cij = 1 if Oi and Oj belong to the same cluster in C; Cij=0 otherwise. University at Buffalo The State University of New York

External Index ¢ A pair of data object (Oi, Oj) falls into one of the following categories q q SS: Cij=1 and Pij=1; DD: Cij=0 and Pij=0; SD: Cij=1 and Pij=0; DS: Cij=0 and Pij=1; (agree) (disagree) ¢ Rand index q may be dominated by DD ¢ Jaccard Coefficient University at Buffalo The State University of New York

Internal Index ¢ “Ground truth” may be unavailable ¢ Use only the data to measure cluster quality q Measure the “homogeneity” and “separation” of clusters. m SSE: Sum of squared errors. q Calculate the correlation between clustering results and distance matrix. University at Buffalo The State University of New York

Sum of Squared Error ¢ Homogeneity is measured by the within cluster sum of squares Exactly the objective function of K-means. ¢ Separation is measured by the between cluster sum of squares Where |Ci| is the size of cluster i, m is the centroid of the whole data set. ¢ BSS + WSS = constant ¢ A larger number of clusters tend to result in smaller WSS. University at Buffalo The State University of New York

Sum of Squared Error 1 m 2 3 K=1 : K=2 : K=4: University at Buffalo The State University of New York 4 m 2 5

Sum of Squared Error ¢ Can also be used to estimate the number of clusters. University at Buffalo The State University of New York

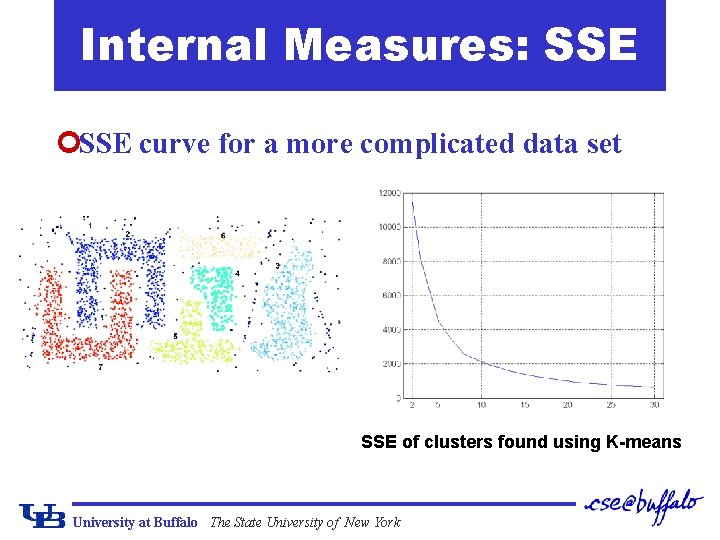
Internal Measures: SSE ¢SSE curve for a more complicated data set SSE of clusters found using K-means University at Buffalo The State University of New York

Correlation with Distance Matrix ¢ Distance Matrix q Dij is the similarity between object Oi and Oj. ¢ Incidence Matrix q Cij=1 if Oi and Oj belong to the same cluster, Cij=0 otherwise ¢ Compute the correlation between the two matrices q. Only n(n-1)/2 entries needs to be calculated. ¢ High correlation indicates good clustering. University at Buffalo The State University of New York

Correlation with Distance Matrix ¢ Given Distance Matrix D = {d 11, d 12, …, dnn } and Incidence Matrix C= { c 11, c 12, …, cnn }. ¢ Correlation r between D and C is given by University at Buffalo The State University of New York

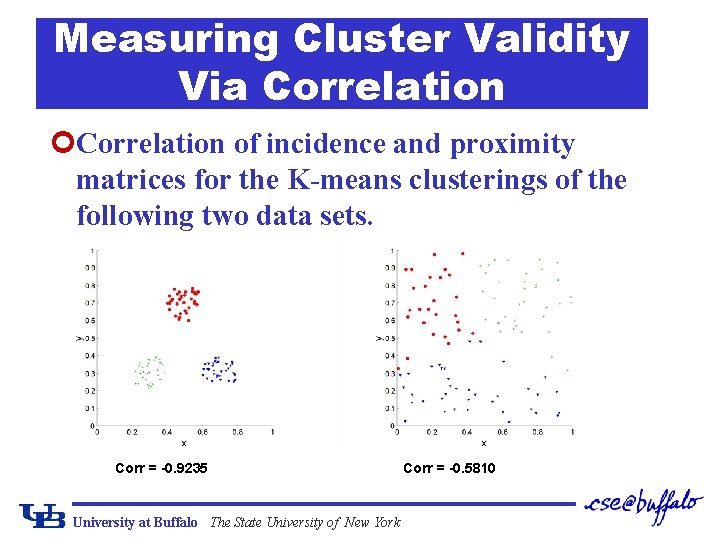
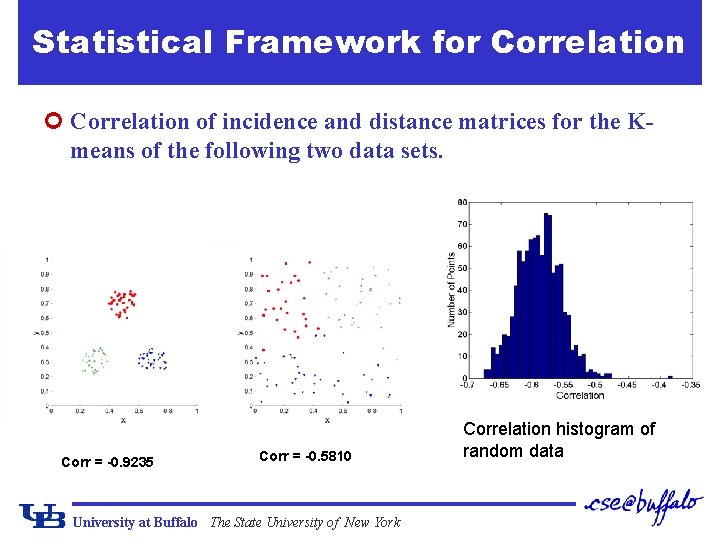
Measuring Cluster Validity Via Correlation ¢Correlation of incidence and proximity matrices for the K-means clusterings of the following two data sets. Corr = -0. 9235 University at Buffalo The State University of New York Corr = -0. 5810

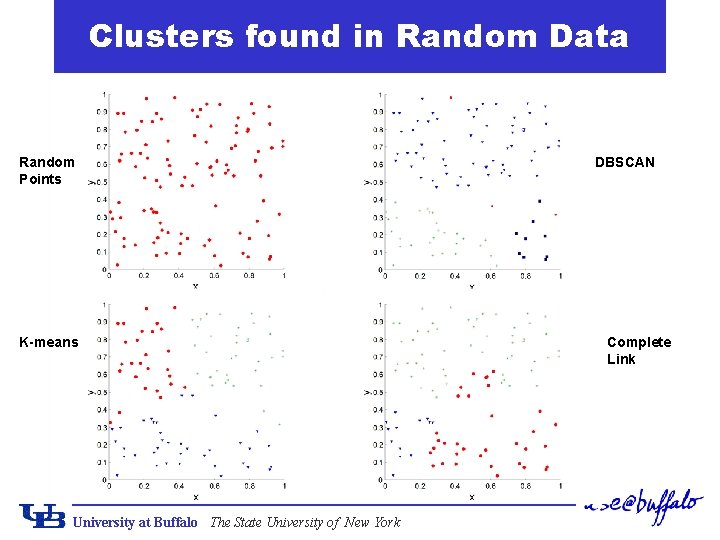
Clusters found in Random Data Random Points K-means University at Buffalo The State University of New York DBSCAN Complete Link

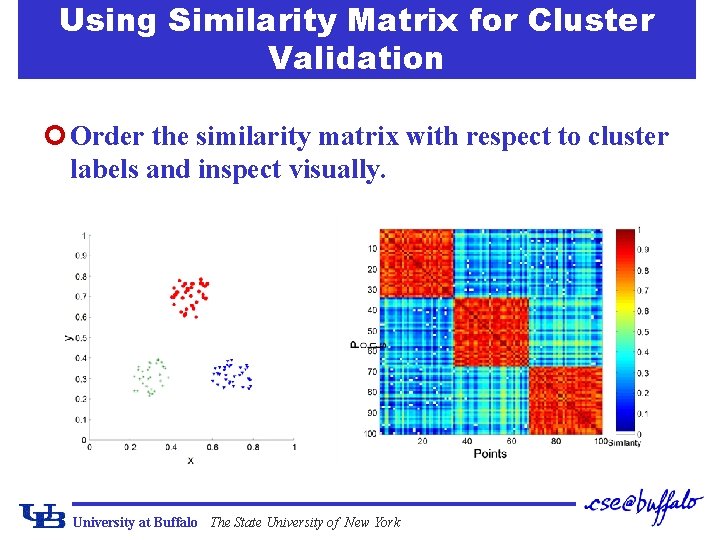
Using Similarity Matrix for Cluster Validation ¢ Order the similarity matrix with respect to cluster labels and inspect visually. University at Buffalo The State University of New York

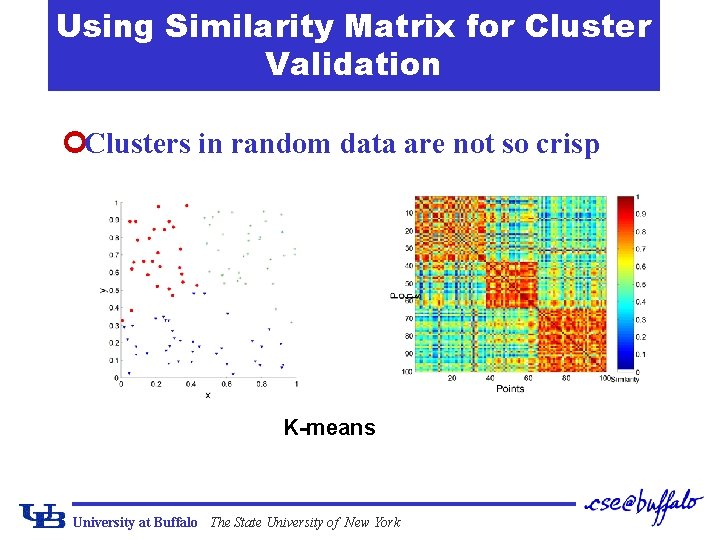
Using Similarity Matrix for Cluster Validation ¢Clusters in random data are not so crisp K-means University at Buffalo The State University of New York

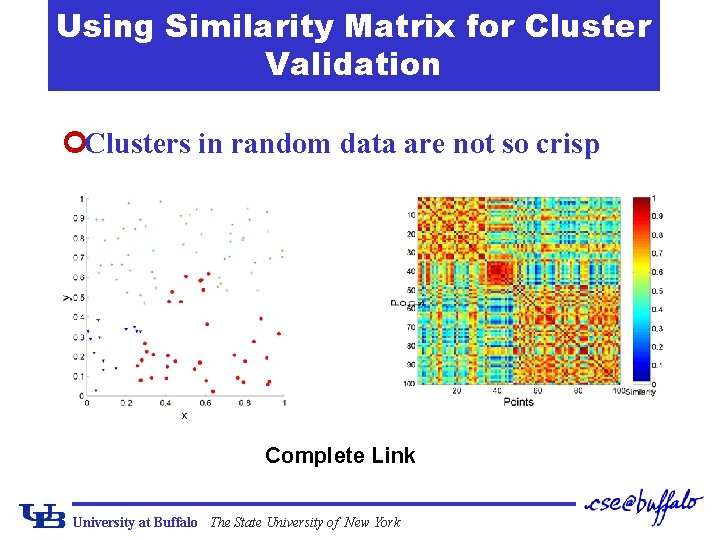
Using Similarity Matrix for Cluster Validation ¢Clusters in random data are not so crisp Complete Link University at Buffalo The State University of New York

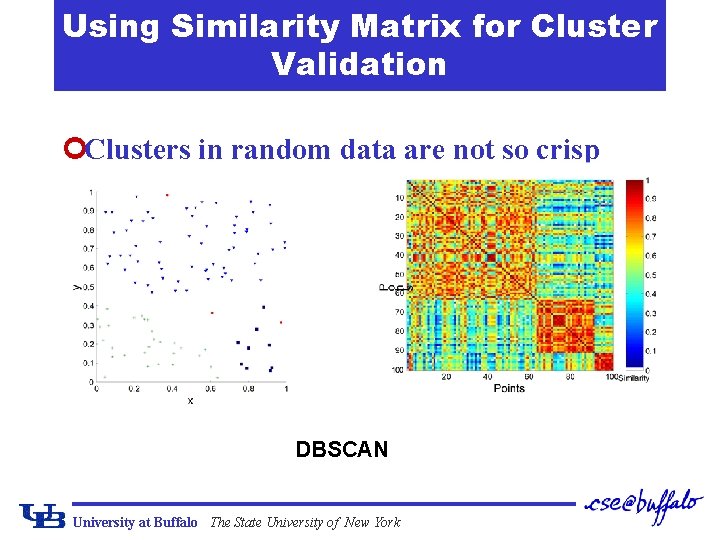
Using Similarity Matrix for Cluster Validation ¢Clusters in random data are not so crisp DBSCAN University at Buffalo The State University of New York

Reliability of Clusters ¢ Need a framework to interpret any measure. q For example, if our measure of evaluation has the value, 10, is that good, fair, or poor? ¢ Statistics provide a framework for cluster validity q The more “atypical” a clustering result is, the more likely it represents valid structure in the data. University at Buffalo The State University of New York

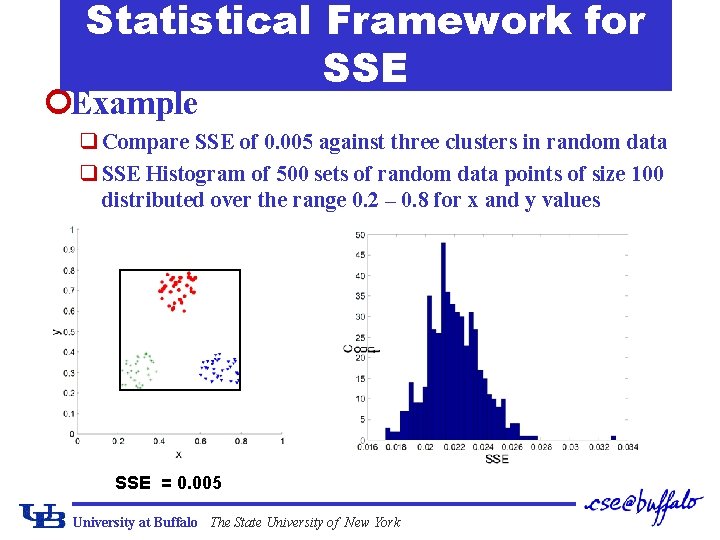
Statistical Framework for SSE ¢Example q Compare SSE of 0. 005 against three clusters in random data q SSE Histogram of 500 sets of random data points of size 100 distributed over the range 0. 2 – 0. 8 for x and y values SSE = 0. 005 University at Buffalo The State University of New York

Statistical Framework for Correlation ¢ Correlation of incidence and distance matrices for the Kmeans of the following two data sets. Corr = -0. 9235 Corr = -0. 5810 University at Buffalo The State University of New York Correlation histogram of random data

Hyper-geometric Distribution ¢ Given the total number of genes in the data set associated with term T is M, if randomly draw n genes from the data set N, what is the probability that m of the selected n genes will be associated with T? University at Buffalo The State University of New York

P-Value Based on Hyper-geometric distribution, the probability of having m genes or fewer associated to T in N can be calculated by summing the probabilities of a random list of N genes having 1, 2, …, m genes associated to T. So the p-value of over-representation is as follows: University at Buffalo The State University of New York