Cluster Strong Lensing Neal Dalal IAS Cluster Strong

Cluster Strong Lensing Neal Dalal IAS

Cluster Strong Lensing • Images of background galaxies strongly distorted by potential of foreground massive cluster • Typically 2 -3 images merged together into “giant arcs” • Canonical giant arcs have l/w > 10 • Usually azimuthally oriented but radial arcs are also observed

Lensing surveys EMSS Comparison of Previous Arc Surveys Redshifts Area (deg 2) Depth Observed 0. 15 < z < 0. 6 ~ 360 V < 22 8 LCDCS 0. 5 < z < 0. 7 69 R < 21. 5 2 z < 0. 6 z > 0. 6 90 90 R < 24 0 4 Survey RCS Ongoing and future surveys (e. g. SDSS, MACS, RCS-2, CFHTLS, DES) increase area and number of detected arcs by many orders of magnitude!

SDSS Arcs

What good are arcs for cosmology? 1. Study properties of clusters • Calibrate mass-observable relations • Measure DM properties (e. g. radial profile, triaxiality, etc. ) 2. Cosmological parameters • Statistics • Geometrical measure

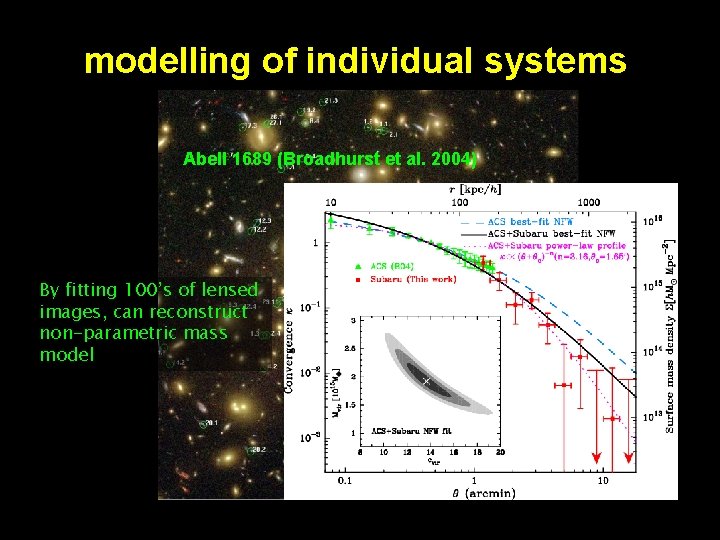
modelling of individual systems Abell 1689 (Broadhurst et al. 2004) By fitting 100’s of lensed images, can reconstruct non-parametric mass model

Strong lens selection Strong lensing can give a precise determination of cluster mass profile. But which clusters are selected with a lens-selected sample? Related: which cluster properties are important in determining lensing cross-section?

Ray Tracing Simulations • Ran 10243 cosmological N-body simulation in 320 h-1 Mpc box • Identify massive cluster halos, measure structural properties Massive Cluster (e. g. ~900 clusters at z=0. 4) • Compute surface density and raytrace from source plane to image plane (~14000 ray-traces for zl=0. 4, zs=1) Lens Plane

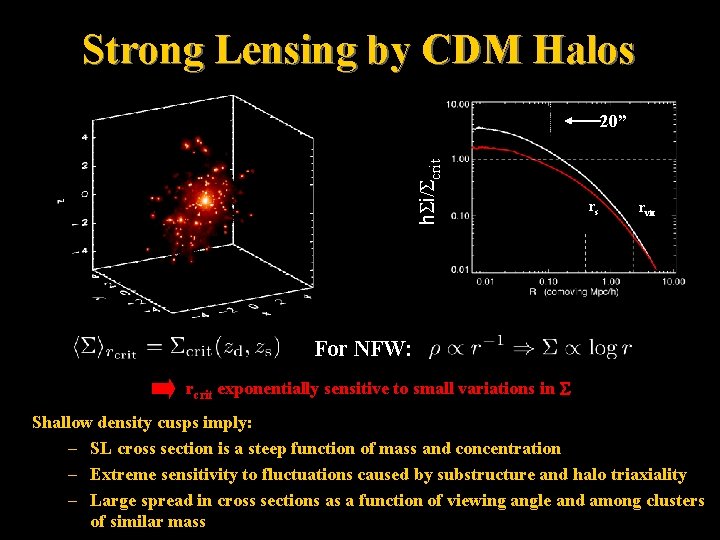
Strong Lensing by CDM Halos h. Si/Scrit 20” rs rvir For NFW: rcrit exponentially sensitive to small variations in Shallow density cusps imply: – SL cross section is a steep function of mass and concentration – Extreme sensitivity to fluctuations caused by substructure and halo triaxiality – Large spread in cross sections as a function of viewing angle and among clusters of similar mass

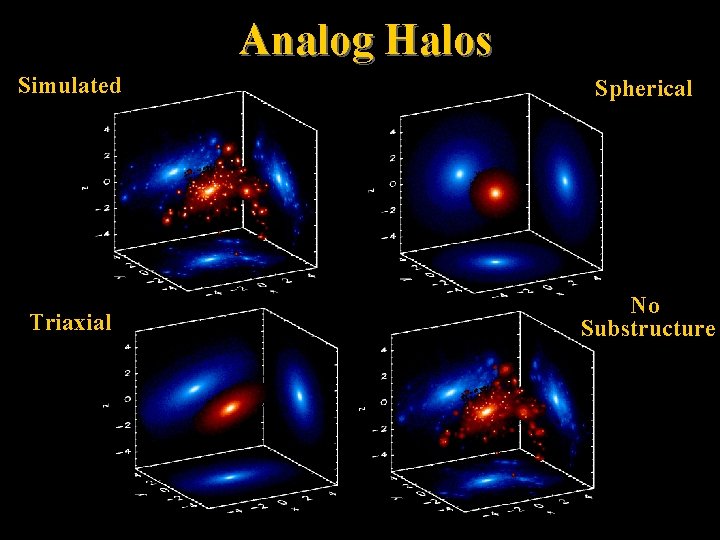
Analog Halos Simulated Spherical Triaxial No Substructure

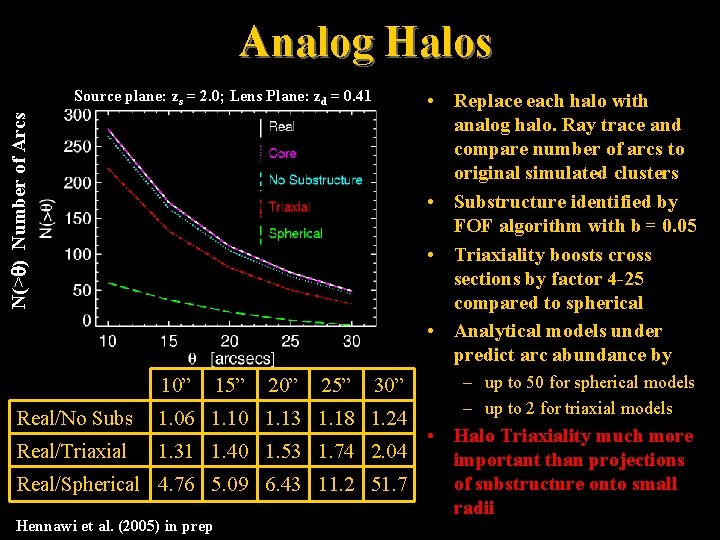
Analog Halos Source plane: zs = 2. 0; Lens Plane: zd = 0. 41 N(> ) Number of Arcs • Replace each halo with analog halo. Ray trace and compare number of arcs to original simulated clusters • Substructure identified by FOF algorithm with b = 0. 05 • Triaxiality boosts cross sections by factor 4 -25 compared to spherical • Analytical models under predict arc abundance by 10” Real/No Subs 15” 20” 25” 30” 1. 06 1. 10 1. 13 1. 18 1. 24 – up to 50 for spherical models – up to 2 for triaxial models • Halo Triaxiality much more Real/Triaxial 1. 31 1. 40 1. 53 1. 74 2. 04 important than projections of substructure onto small Real/Spherical 4. 76 5. 09 6. 43 11. 2 51. 7 radii Hennawi et al. (2005) in prep

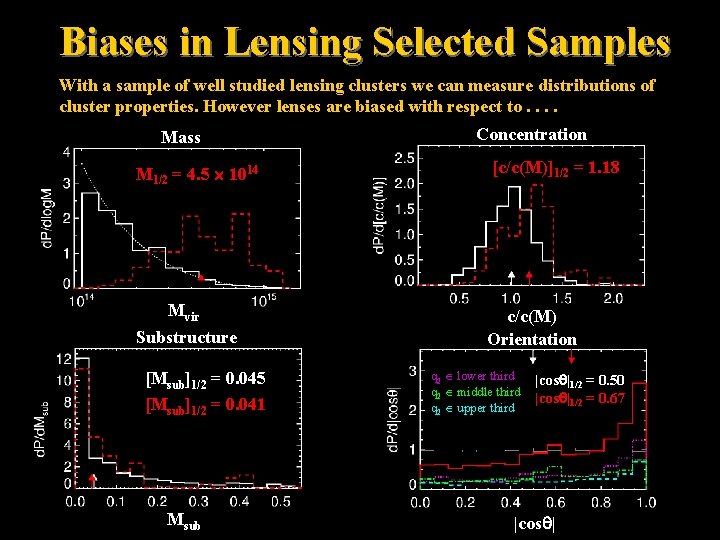
Biases in Lensing Selected Samples With a sample of well studied lensing clusters we can measure distributions of cluster properties. However lenses are biased with respect to. . Mass M 1/2 = 4. 5 1014 Mvir Substructure [Msub]1/2 = 0. 045 [Msub]1/2 = 0. 041 Msub Concentration [c/c(M)]1/2 = 1. 18 c/c(M) Orientation q 2 lower third q 2 middle third q 2 upper third |cos |1/2 = 0. 50 |cos |1/2 = 0. 67 |cos |

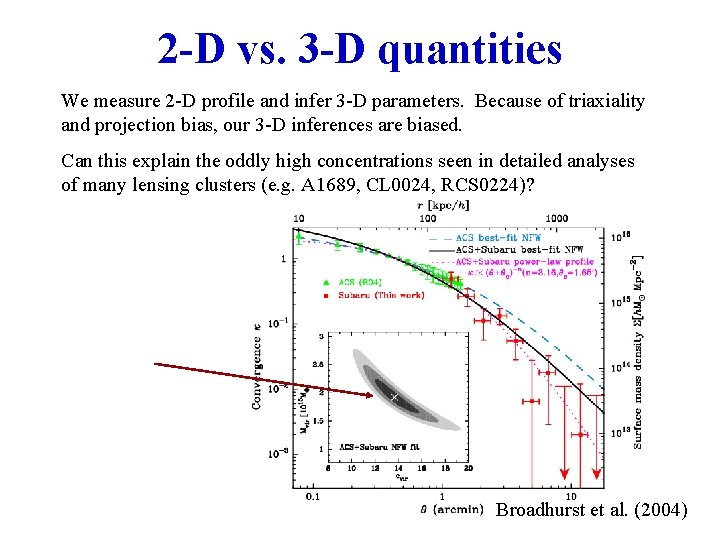
2 -D vs. 3 -D quantities We measure 2 -D profile and infer 3 -D parameters. Because of triaxiality and projection bias, our 3 -D inferences are biased. Can this explain the oddly high concentrations seen in detailed analyses of many lensing clusters (e. g. A 1689, CL 0024, RCS 0224)? Broadhurst et al. (2004)

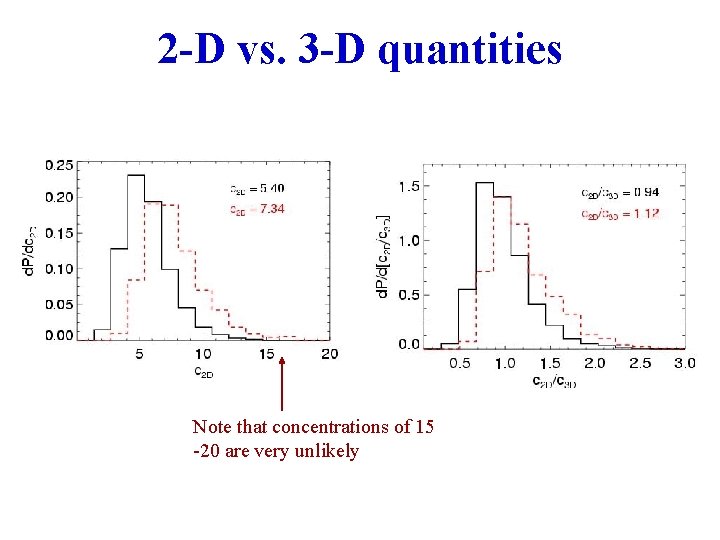
2 -D vs. 3 -D quantities Note that concentrations of 15 -20 are very unlikely

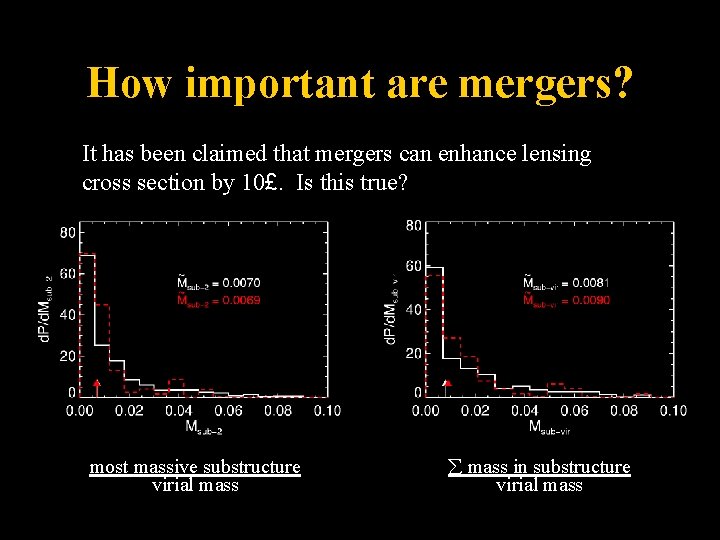
How important are mergers? It has been claimed that mergers can enhance lensing cross section by 10£. Is this true? most massive substructure virial mass å mass in substructure virial mass

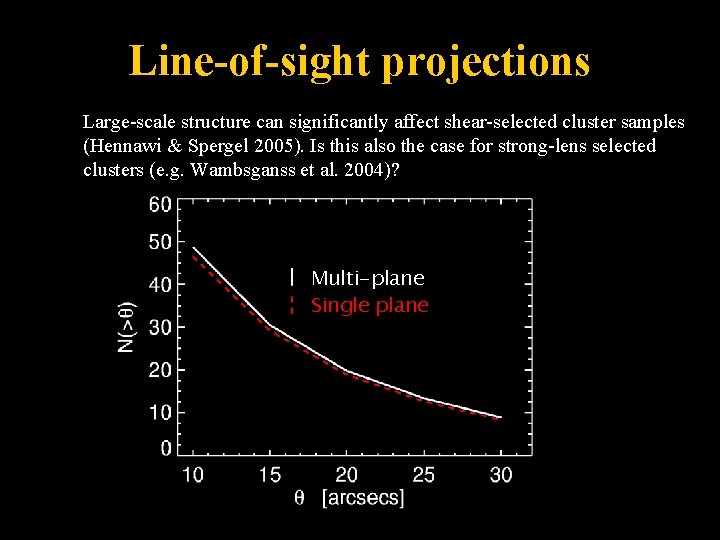
Line-of-sight projections Large-scale structure can significantly affect shear-selected cluster samples (Hennawi & Spergel 2005). Is this also the case for strong-lens selected clusters (e. g. Wambsganss et al. 2004)? Multi-plane Single plane

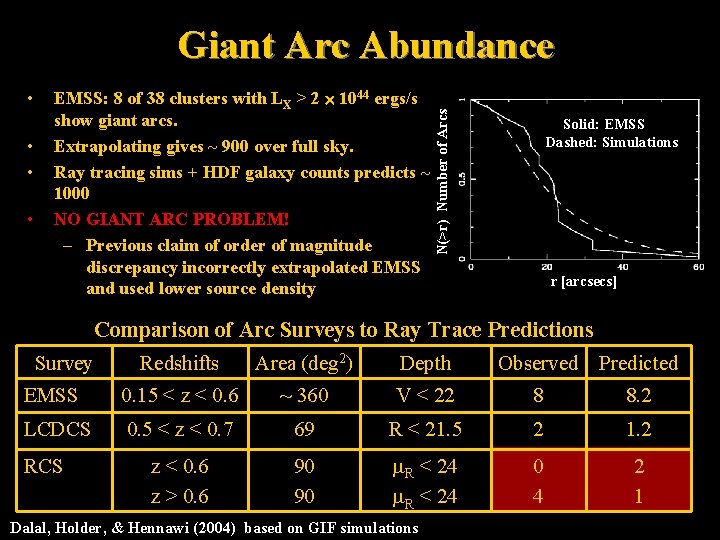
• • EMSS: 8 of 38 clusters with LX > 2 1044 ergs/s show giant arcs. Extrapolating gives ~ 900 over full sky. Ray tracing sims + HDF galaxy counts predicts ~ 1000 NO GIANT ARC PROBLEM! – Previous claim of order of magnitude discrepancy incorrectly extrapolated EMSS and used lower source density N(>r) Number of Arcs Giant Arc Abundance Solid: EMSS Dashed: Simulations r [arcsecs] Comparison of Arc Surveys to Ray Trace Predictions Survey Redshifts Area (deg 2) Depth Observed Predicted EMSS 0. 15 < z < 0. 6 ~ 360 V < 22 8 8. 2 LCDCS RCS 0. 5 < z < 0. 7 69 R < 21. 5 2 1. 2 z < 0. 6 z > 0. 6 90 90 R < 24 0 4 2 1 Dalal, Holder, & Hennawi (2004) based on GIF simulations

Conclusions • Cluster lensing is a powerful probe of the distribution of dark matter on ~ 100 kpc/h scales • Shallow density cusps of CDM clusters imply SL cross sections are extremely sensitive to ellipticity/triaxiality of dark matter halos • Abundance of giant arcs behind low-z clusters agrees with prediction for LCDM. Hint of an excess for high-z clusters (Gladders/RCS) • Search for clusters lenses in SDSS Gpc 3 volume will yield > 200 new giant arcs and ~ 8 new wide separation multiply image quasars

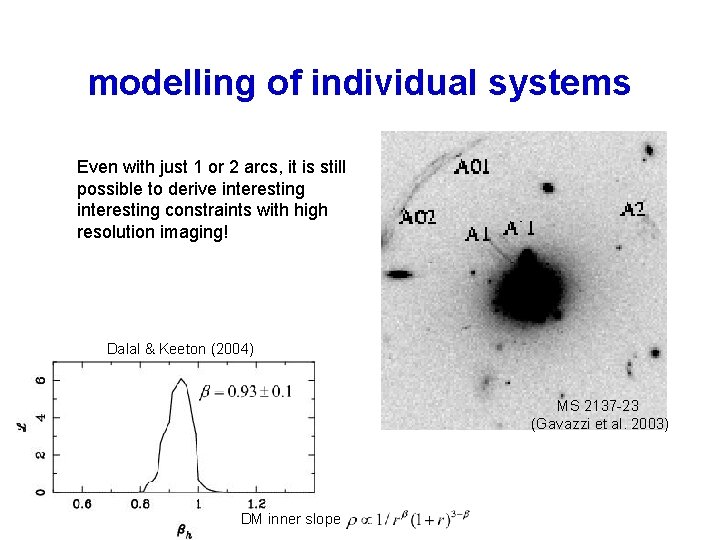
modelling of individual systems Even with just 1 or 2 arcs, it is still possible to derive interesting constraints with high resolution imaging! Dalal & Keeton (2004) MS 2137 -23 (Gavazzi et al. 2003) DM inner slope

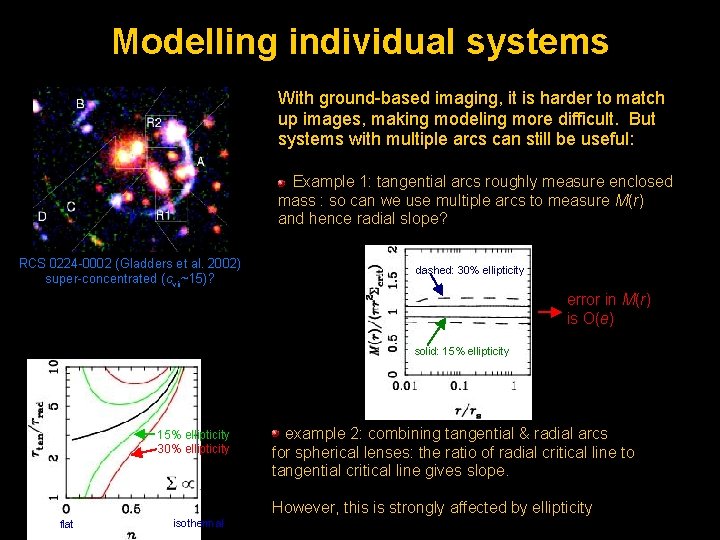
Modelling individual systems With ground-based imaging, it is harder to match up images, making modeling more difficult. But systems with multiple arcs can still be useful: Example 1: tangential arcs roughly measure enclosed mass : so can we use multiple arcs to measure M(r) and hence radial slope? RCS 0224 -0002 (Gladders et al. 2002) super-concentrated (cvir~15)? dashed: 30% ellipticity error in M(r) is O(e) solid: 15% ellipticity 30% ellipticity example 2: combining tangential & radial arcs for spherical lenses: the ratio of radial critical line to tangential critical line gives slope. However, this is strongly affected by ellipticity flat isothermal

Cluster Lenses in the SDSS Multiply Imaged Quasars Giant Arcs WIYN 3. 5 m SDSS 2. 5 m UH 2. 2 m ARC 3. 5 m Jim Gunn Apache Point Observatory • SDSS cluster sample • • – Richness selected clusters out to z < 0. 6 -- 7000 deg 2 or ~ Gpc 3 • – Photo-z’s good to within dz = 0. 02 Deep imaging ( g < 26) of richest clusters • on 4 m class imagers Arc redshifts from Magellan and MMT HST imaging of lenses discovered? SDSS quasar samples – Spectro: 50, 000 quasars -- 4000 deg 2 – Photo: 400, 000 quasars -- 7000 deg 2 Search for companions around quasars with similar colors Follow up spectroscopy (ARC 3. 5 m) required because of fiber collisions

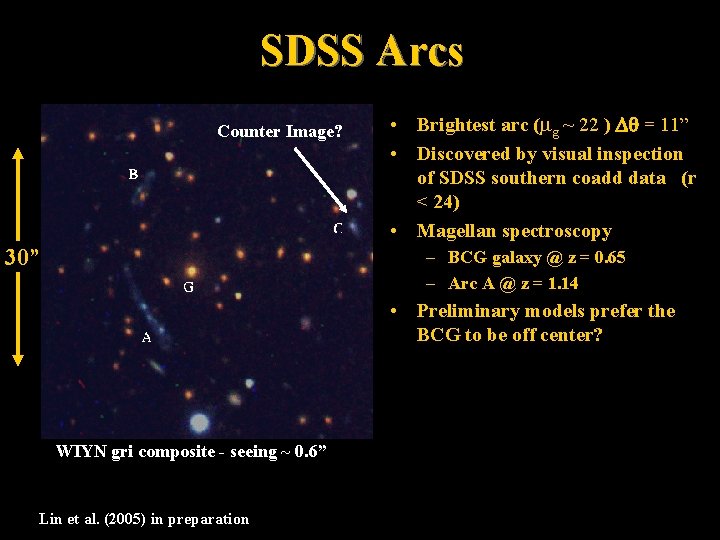
SDSS Arcs Counter Image? 30” • Brightest arc ( g ~ 22 ) = 11” • Discovered by visual inspection of SDSS southern coadd data (r < 24) • Magellan spectroscopy – BCG galaxy @ z = 0. 65 – Arc A @ z = 1. 14 • Preliminary models prefer the BCG to be off center? WIYN gri composite - seeing ~ 0. 6” Lin et al. (2005) in preparation Extreme example of minor axis cusp? Or instead, is BCG off-center?

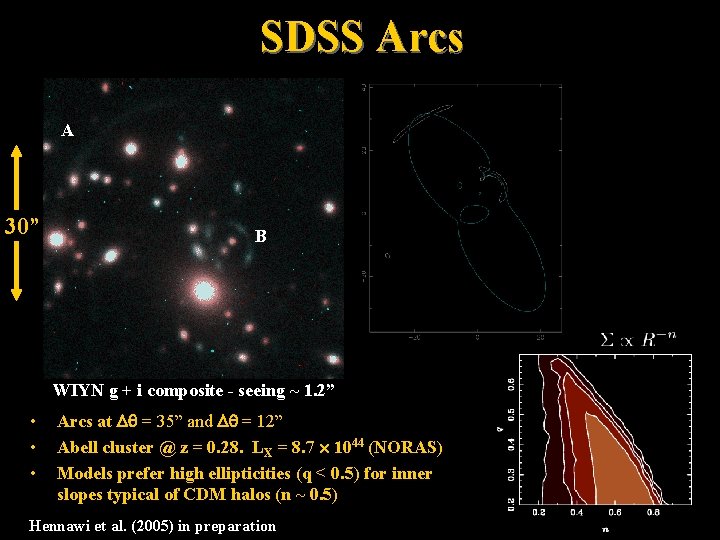
SDSS Arcs A 30” B WIYN g + i composite - seeing ~ 1. 2” • • • Arcs at = 35” and = 12” Abell cluster @ z = 0. 28. LX = 8. 7 1044 (NORAS) Models prefer high ellipticities (q < 0. 5) for inner slopes typical of CDM halos (n ~ 0. 5) Hennawi et al. (2005) in preparation

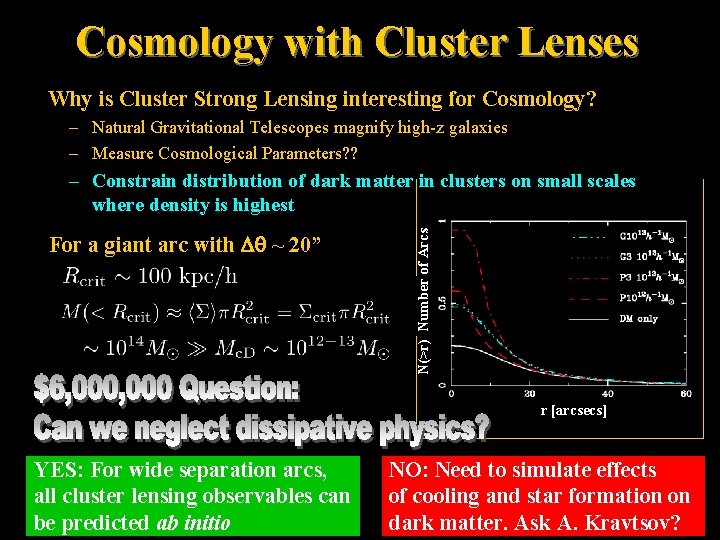
Cosmology with Cluster Lenses Why is Cluster Strong Lensing interesting for Cosmology? – Natural Gravitational Telescopes magnify high-z galaxies – Measure Cosmological Parameters? ? For a giant arc with ~ 20” N(>r) Number of Arcs – Constrain distribution of dark matter in clusters on small scales where density is highest r [arcsecs] YES: For wide separation arcs, all cluster lensing observables can be predicted ab initio NO: Need to simulate effects of cooling and star formation on dark matter. Ask A. Kravtsov?

Strong Lensing Statistics Abundance – Count the number of lensed arcs (QSOs? ) per deg 2 as a function of angular separation and compare to prediction from N-body sims • • PROS Simplest ‘one-point’ statistic Requires ground based imaging of most massive clusters • • CONS Arcs identified by eye. Selection function very difficult to quantify (QSOs? ) Uncertainty in cluster mass scale creeps in unless entire survey area is deeply imaged Detailed Modeling of Individual Lenses – Measure structural parameters of cluster (concentration, ellipticity/triaxiality, inner slope) for each cluster lens. Compare to analogous distributions in N-body simulations • • PROS Isolates parameters of halos breaking • ‘degeneracies’ which could produce the same abundance • Does not require knowledge of selection function of arcs CONS Requires multiple arcs. Imaging from space required to obtain tight constraints Even with multiple arcs degeneracies between model parameters complicates comparison to simulations