Cluster DMFT studies of the Mott transition of

Cluster DMFT studies of the Mott transition of Kappa Organics and Cuprates. G. Kotliar Physics Department and Center for Materials Theory Rutgers La Jolla San Diego May 2005

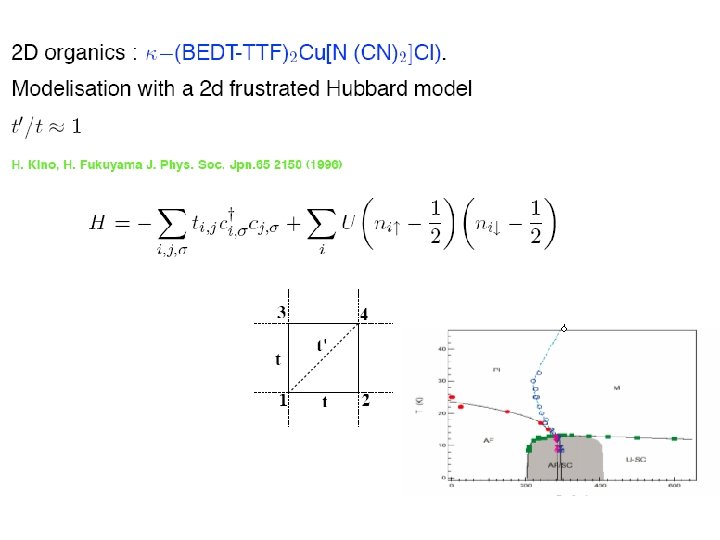
Outline o Dynamical Mean Field Theory and a cluster extension, CDMFT: G. . Kotliar, S. Savrasov, G. Palsson and G. Biroli, Phys. Rev. Lett. 87, 186401 (2001) o Model for kappa organics. [O. Parcollet, G. Biroli and G. Kotliar PRL, 92, 226402. (2004)) ] o Model for cuprates [O. Parcollet (Saclay), M. Capone (U. Rome) M. Civelli (Rutgers) V. Kancharla (Sherbrooke) GK(2005).

Model Hamiltonians: Hubbard model q. U/t q. Doping d or chemical potential q. Frustration (t’/t) q. T temperature

Limit of large lattice coordination Metzner Vollhardt, 89 Muller-Hartmann 89

Mean-Field Classical vs Quantum Classical case Quantum case A. Georges, G. Kotliar Phys. Rev. B 45, 6497(1992)

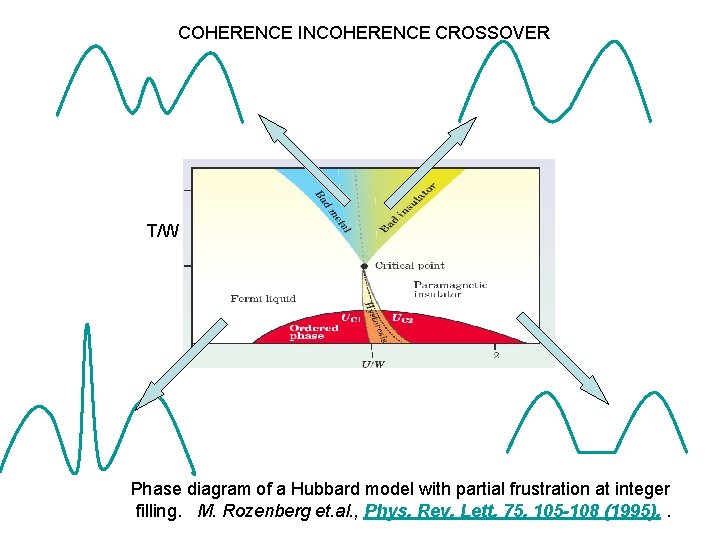
COHERENCE INCOHERENCE CROSSOVER T/W Phase diagram of a Hubbard model with partial frustration at integer filling. M. Rozenberg et. al. , Phys. Rev. Lett. 75, 105 -108 (1995). .

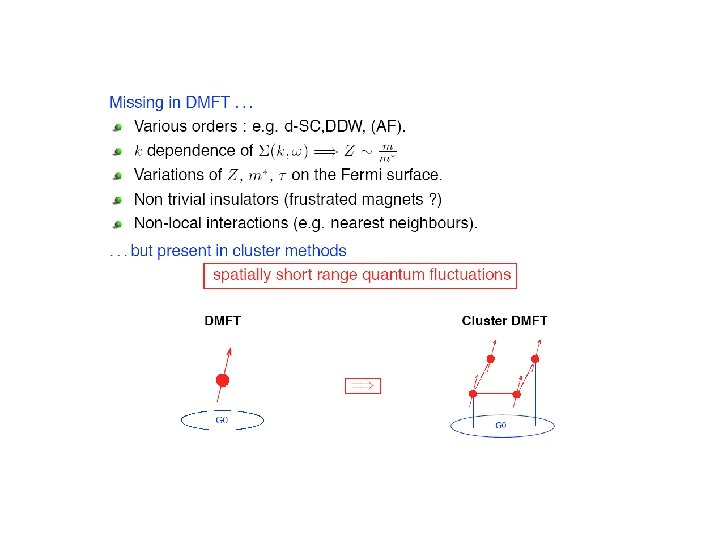
Medium of free electrons : impurity model. Solve for the medium using Self Consistency G. . Kotliar, S. Savrasov, G. Palsson and G. Biroli, Phys. Rev. Lett. 87, 186401 (2001)

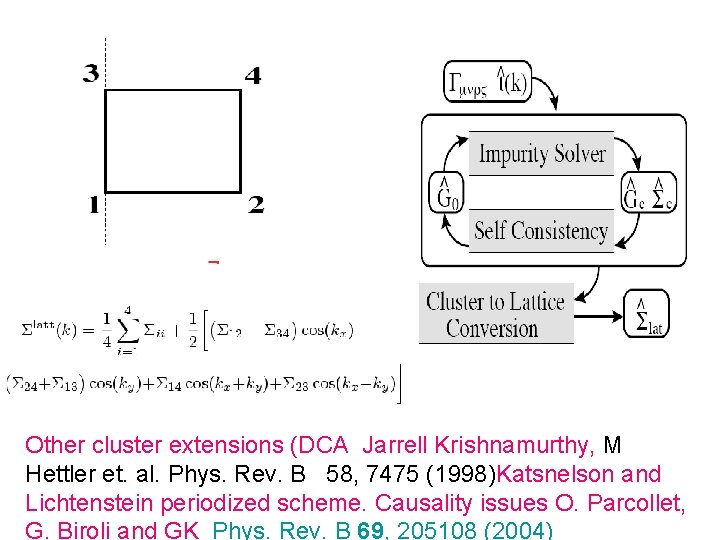
Other cluster extensions (DCA Jarrell Krishnamurthy, M Hettler et. al. Phys. Rev. B 58, 7475 (1998)Katsnelson and Lichtenstein periodized scheme. Causality issues O. Parcollet, G. Biroli and GK Phys. Rev. B 69, 205108 (2004)

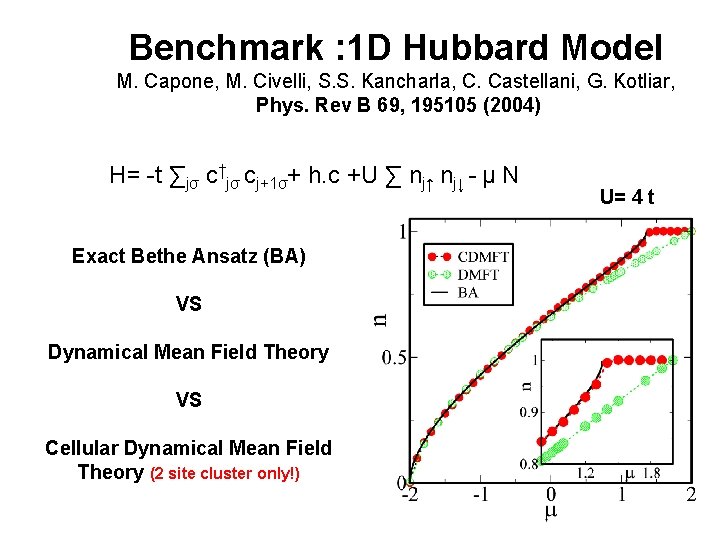
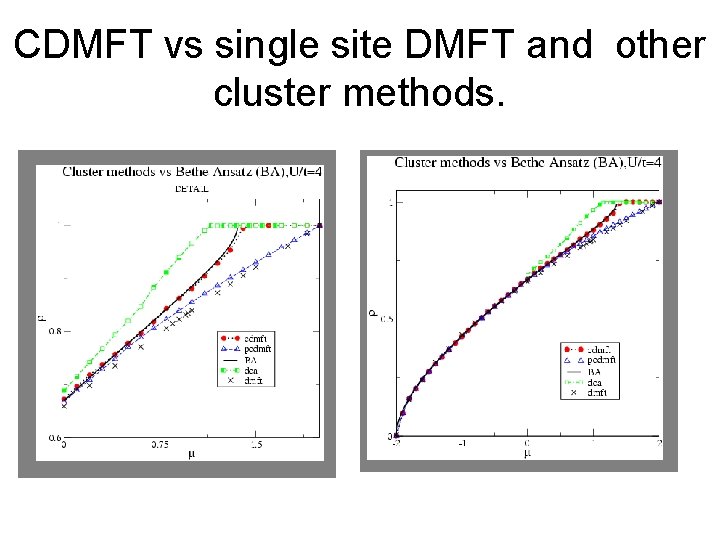
Benchmark : 1 D Hubbard Model M. Capone, M. Civelli, S. S. Kancharla, C. Castellani, G. Kotliar, Phys. Rev B 69, 195105 (2004) H= -t ∑jσ c†jσ cj+1σ+ h. c +U ∑ nj↑ nj↓ - μ N Exact Bethe Ansatz (BA) VS Dynamical Mean Field Theory VS Cellular Dynamical Mean Field Theory (2 site cluster only!) U= 4 t

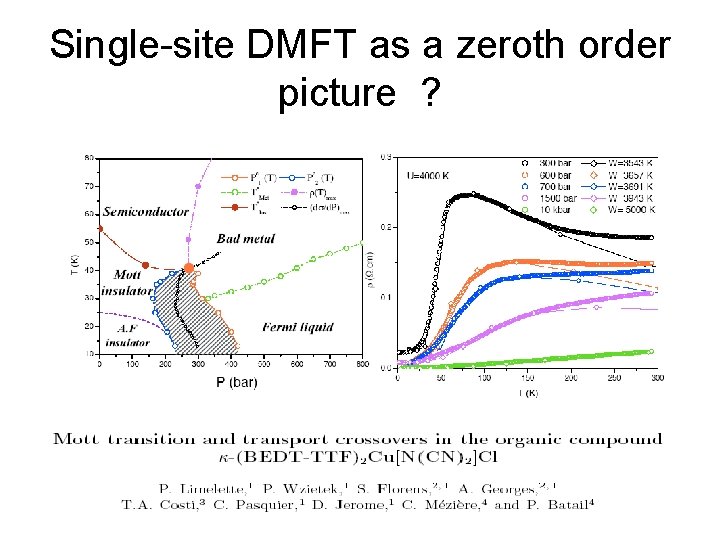
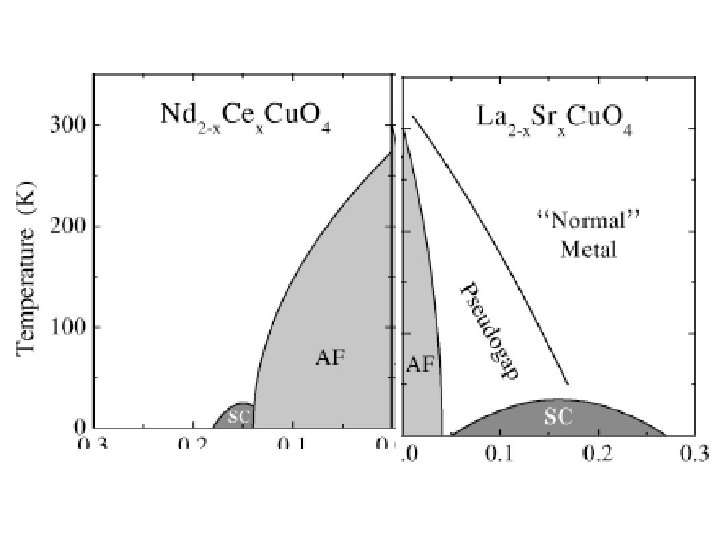
Mott transition in layered organic conductors -mat/0004455, Phys. Rev. Lett. 85, 5420 (2000) S Lefebvre et al. cond

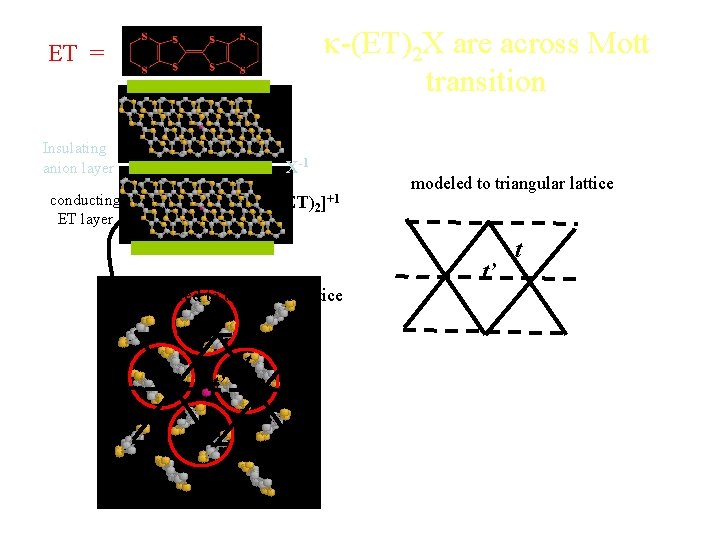
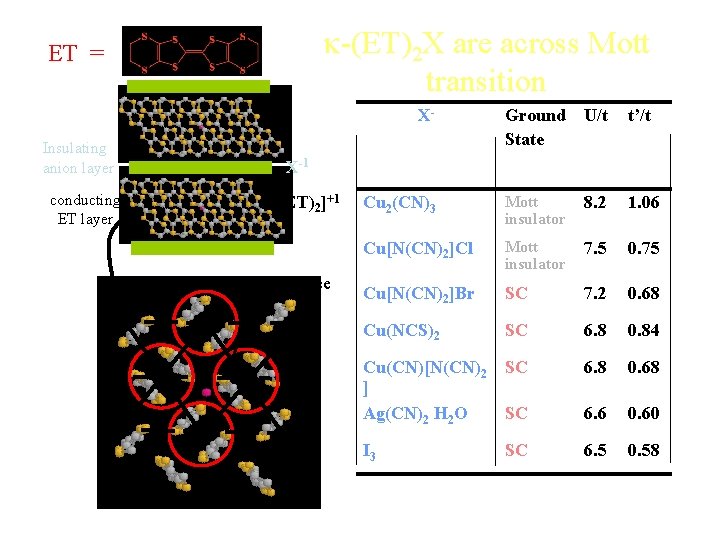
k-(ET)2 X are across Mott transition ET = Insulating anion layer X-1 conducting ET layer [(ET)2 ]+1 modeled to triangular lattice t’ t t

Single-site DMFT as a zeroth order picture ?

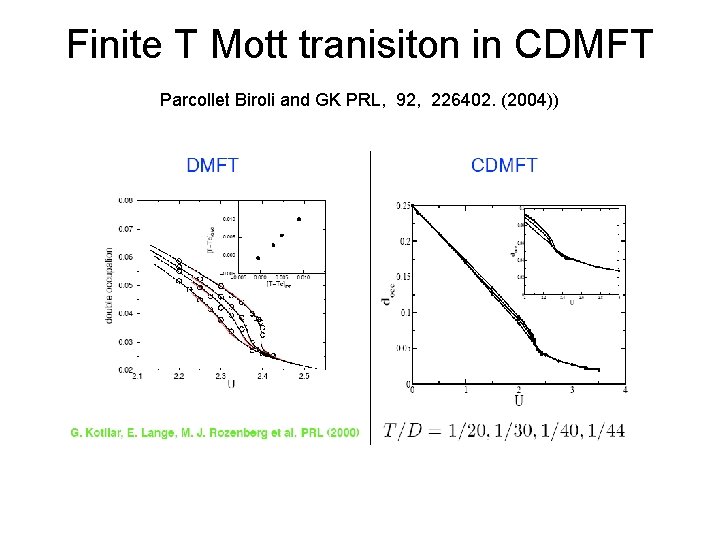
Finite T Mott tranisiton in CDMFT Parcollet Biroli and GK PRL, 92, 226402. (2004))

Evolution of the spectral function at low frequency. If the k dependence of the self energy is weak, we expect to see contour lines corresponding to t(k) = const and a height increasing as we approach the

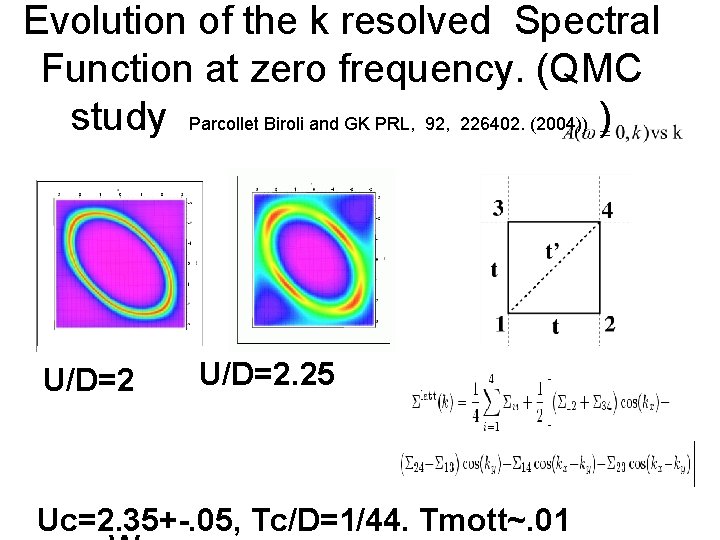
Evolution of the k resolved Spectral Function at zero frequency. (QMC study Parcollet Biroli and GK PRL, 92, 226402. (2004)) ) U/D=2. 25 Uc=2. 35+-. 05, Tc/D=1/44. Tmott~. 01

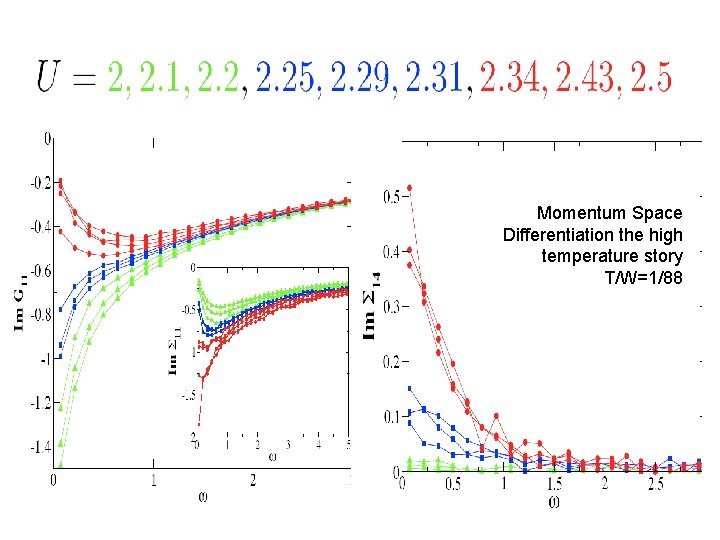
Momentum Space Differentiation the high temperature story T/W=1/88

CDMFT study of cuprates. • Allows the investigation of the normal state underlying the superconducting state, by forcing a symmetric Weiss function, we can follow the normal state near the Mott transition. • Earlier studies (Katsnelson and Lichtenstein, M. Jarrell, M Hettler et. al. Phys. Rev. B 58, 7475 (1998). T. Maier et. al. Phys. Rev. Lett 85, ) used QMC as an impurity solver and DCA as cluster scheme. • We use exact diag ( Krauth Caffarel 1995 with effective temperature 32/t=124/D ) as a solver and Cellular DMFT as the mean field scheme. 1524 (2000)

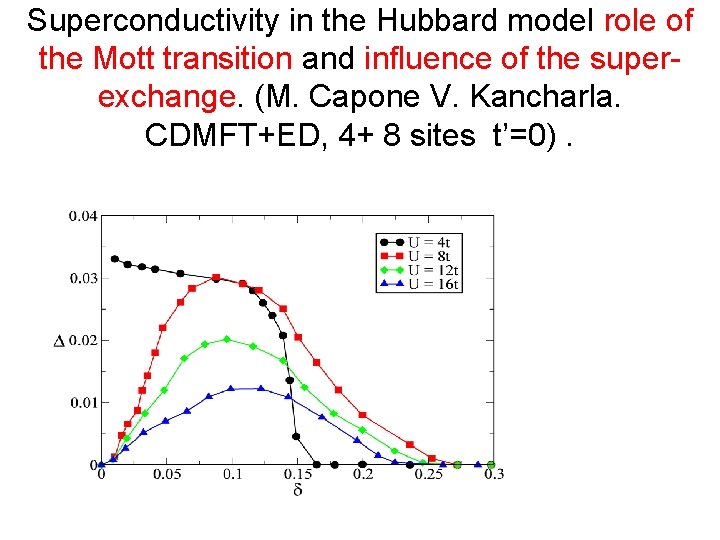
Superconductivity in the Hubbard model role of the Mott transition and influence of the superexchange. (M. Capone V. Kancharla. CDMFT+ED, 4+ 8 sites t’=0).

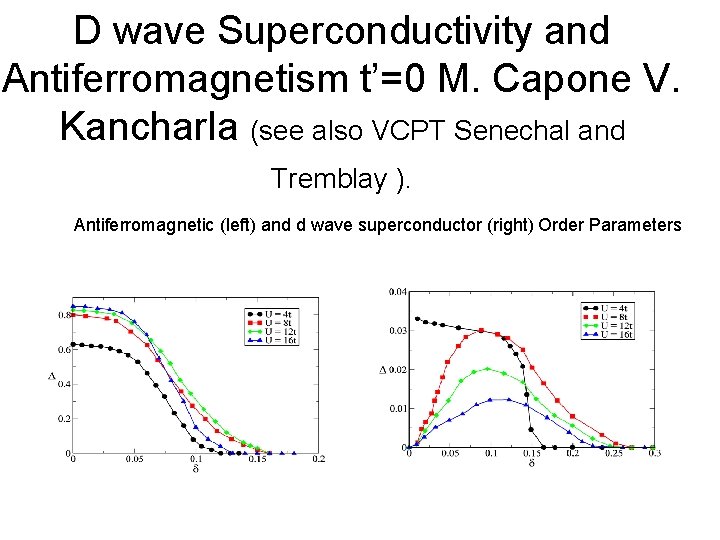
D wave Superconductivity and Antiferromagnetism t’=0 M. Capone V. Kancharla (see also VCPT Senechal and Tremblay ). Antiferromagnetic (left) and d wave superconductor (right) Order Parameters

Follow the “normal state” with doping. Evolution of the spectral function at low frequency. If the k dependence of the self energy is weak, we expect to see contour lines corresponding to Ek = const and a height increasing as we approach the

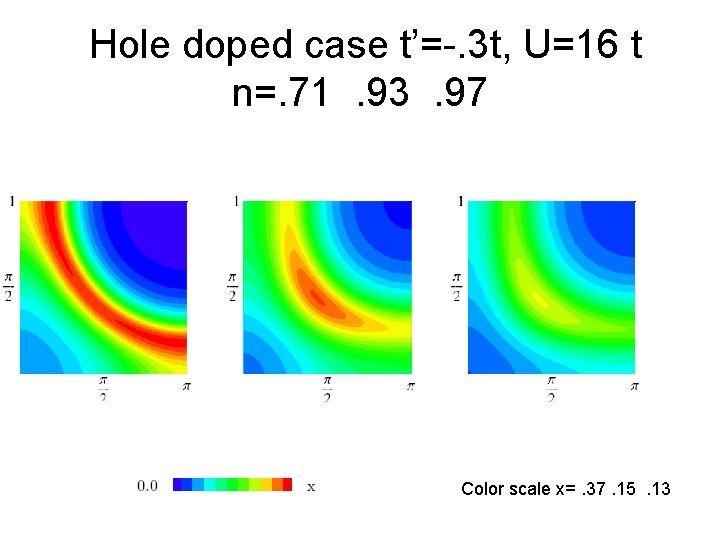
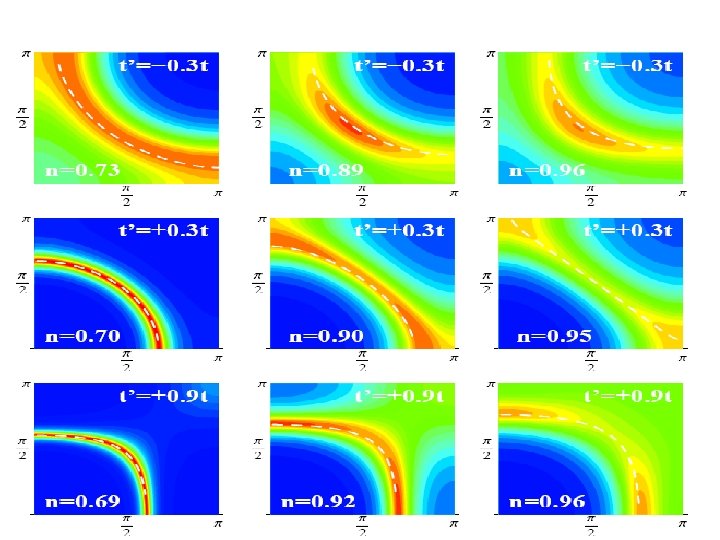
Hole doped case t’=-. 3 t, U=16 t n=. 71. 93. 97 Color scale x=. 37. 15. 13

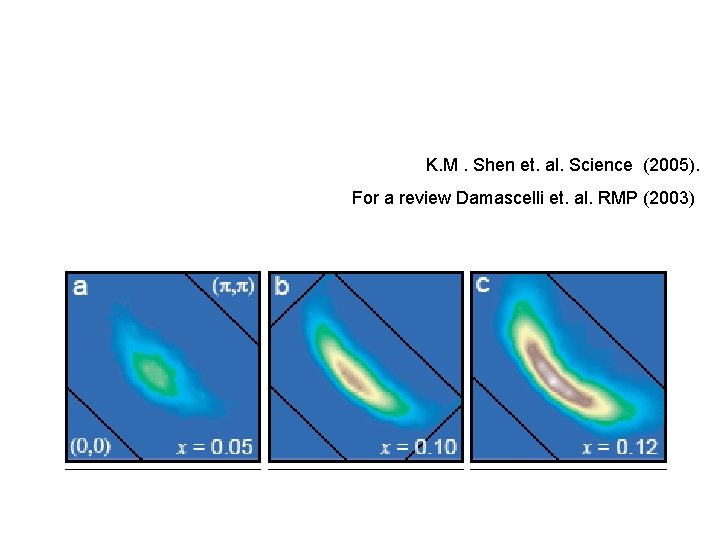
K. M. Shen et. al. Science (2005). For a review Damascelli et. al. RMP (2003)

Approaching the Mott transition: CDMFT Picture • Qualitative effect, momentum space differentiation. Formation of hot –cold regions is an unavoidable consequence of the approach to the Mott insulating state! • D wave gapping of the single particle spectra as the Mott transition is approached. • Similar scenario was encountered in previous study of the kappa organics. O Parcollet G. Biroli and G. Kotliar PRL, 92, 226402. (2004).

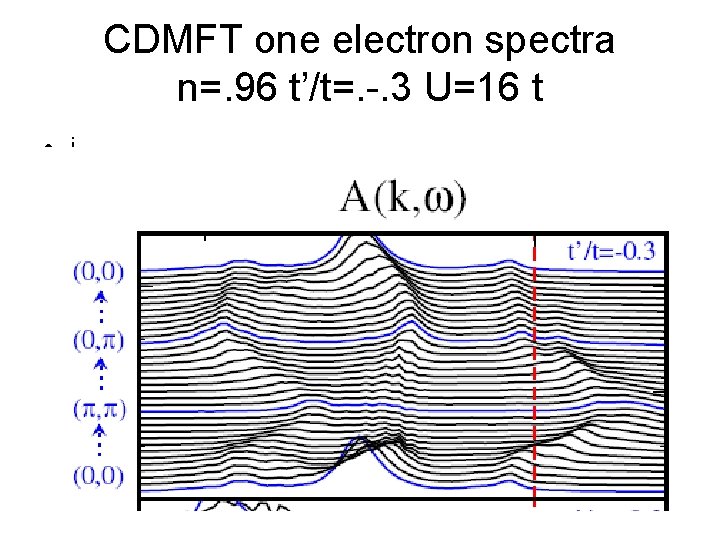
CDMFT one electron spectra n=. 96 t’/t=. -. 3 U=16 t • i

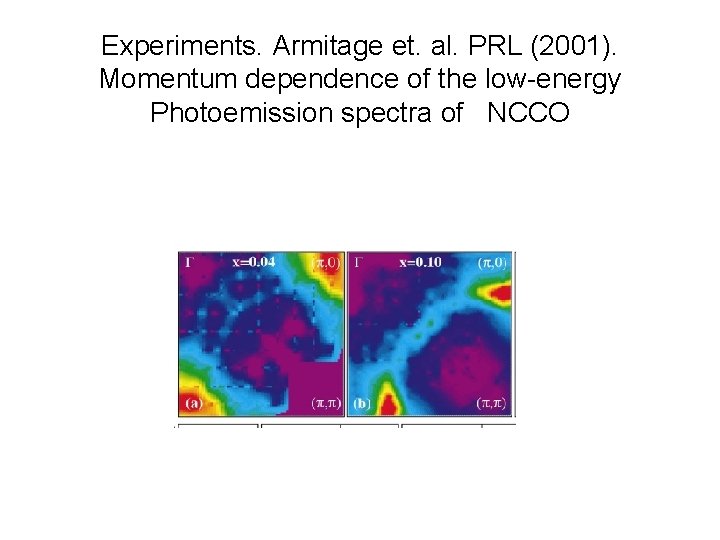
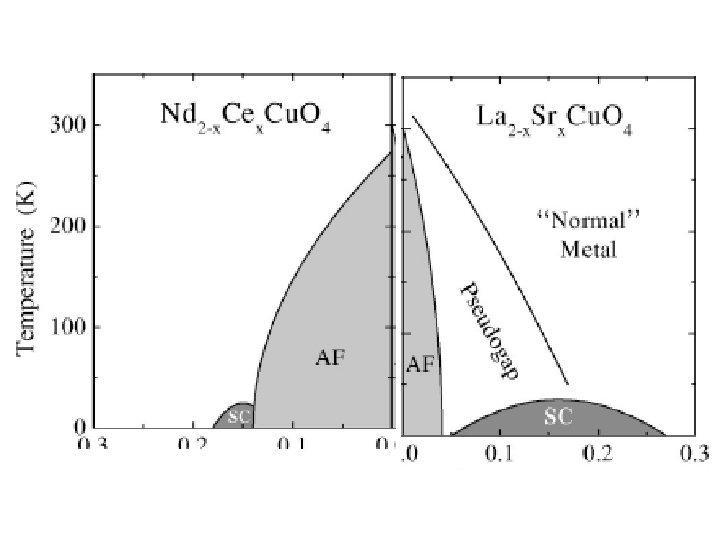
Experiments. Armitage et. al. PRL (2001). Momentum dependence of the low-energy Photoemission spectra of NCCO

Approaching the Mott transition: CDMFT picture. • Qualitative effect, momentum space differentiation. Formation of hot –cold regions is an unavoidable consequence of the approach to the Mott insulating state! • General phenomena, BUT the location of the cold regions depends on parameters. • Quasiparticles are now generated from the Mott insulator at (p, 0). • Results of many numerical studies of electron hole asymmetry in t-t’ Hubbard models Tohyama Maekawa Phys. Rev. B 67, 092509 (2003) Senechal and Tremblay. PRL 92 126401 (2004) Kusko et. al. Phys. Rev 66, 140513 (2002)…………

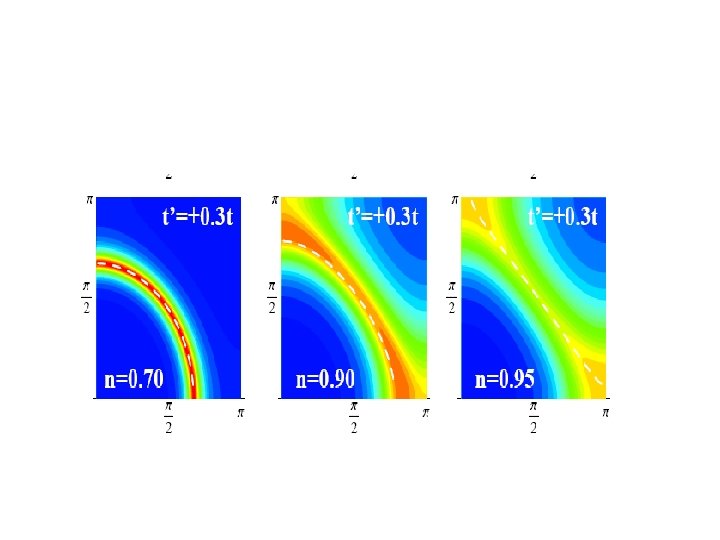
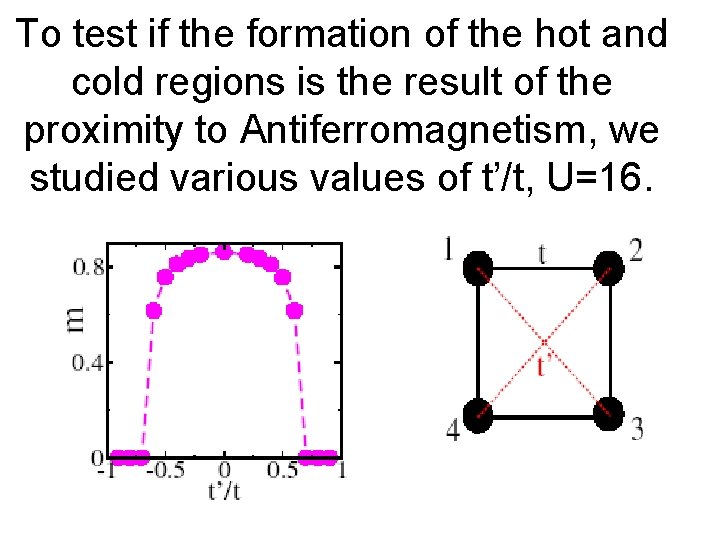
To test if the formation of the hot and cold regions is the result of the proximity to Antiferromagnetism, we studied various values of t’/t, U=16.

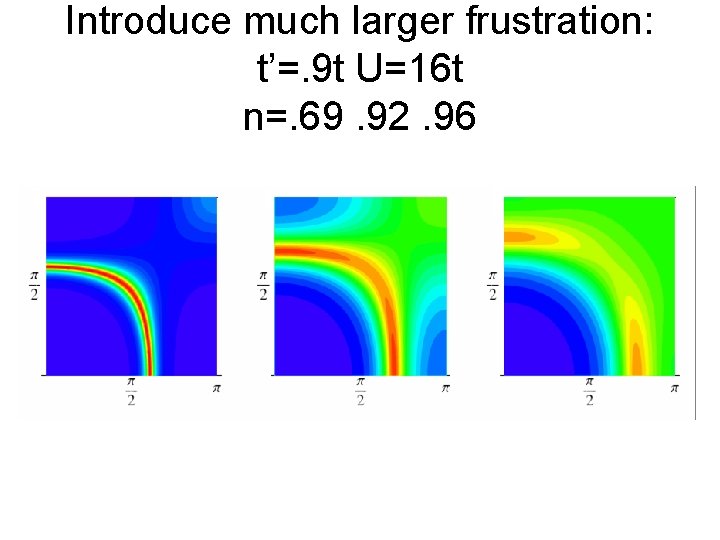
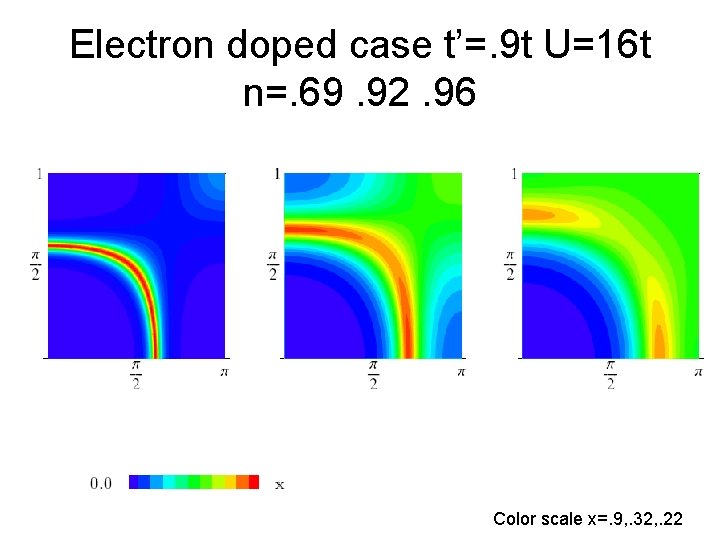
Introduce much larger frustration: t’=. 9 t U=16 t n=. 69. 92. 96

Approaching the Mott transition: • Qualitative effect, momentum space differentiation. Formation of hot –cold regions is an unavoidable consequence of the approach to the Mott insulating state! • General phenomena, but the location of the cold regions depends on parameters. • With the present resolution, t’ =. 9 and. 3 are similar. However it is perfectly possible that at lower energies further refinements and differentiation will result from the proximity to different ordered states.

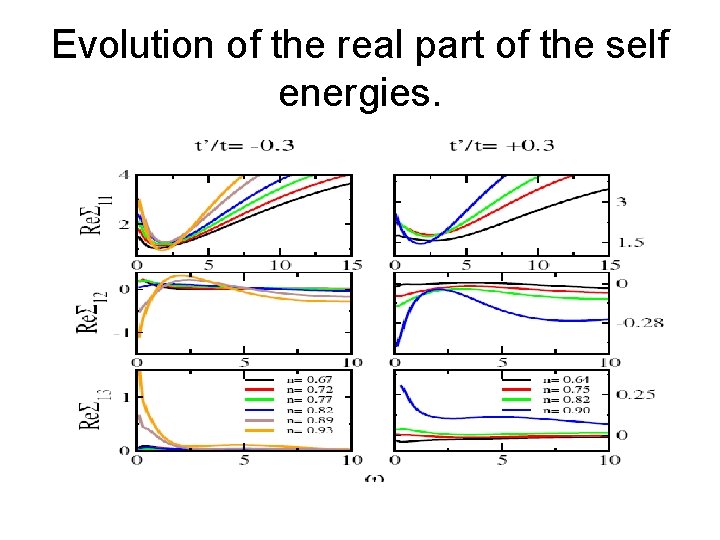
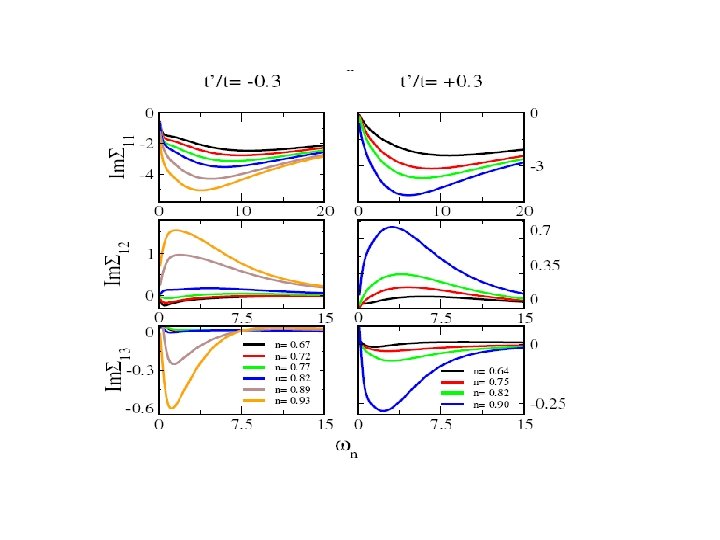
Evolution of the real part of the self energies.

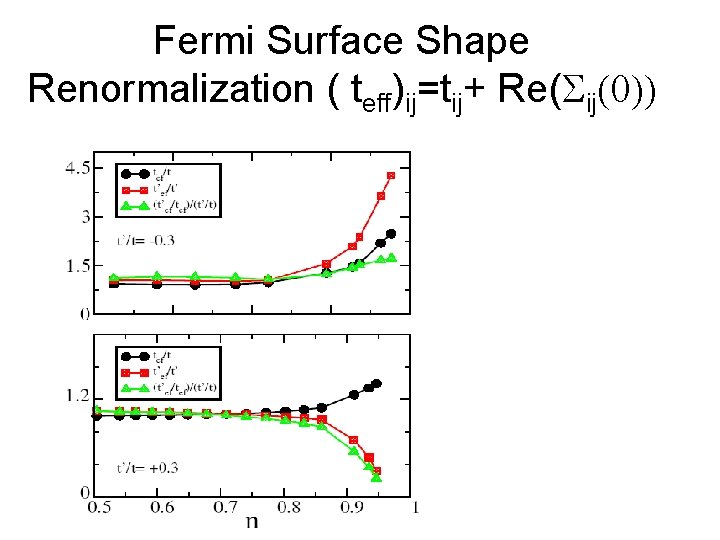
Fermi Surface Shape Renormalization ( teff)ij=tij+ Re(Sij(0))

Fermi Surface Shape Renormalization • Photoemission measured the low energy renormalized Fermi surface. • If the high energy (bare ) parameters are doping independent, then the low energy hopping parameters are doping dependent. Another failure of the rigid band picture. • Electron doped case, the Fermi surface renormalizes TOWARDS nesting, the hole doped case the Fermi surface renormalizes AWAY from nesting. Enhanced magnetism in the electron doped side.

o Qualitative Difference between the hole doped and the electron doped phase diagram is due to the underlying normal state. ” In the hole doped, it has nodal quasiparticles near (p/2, p/2) which are ready “to become the superconducting quasiparticles”. Therefore the superconducing state can evolve continuously to the normal state. The superconductivity can appear at very small doping. o Electron doped case, has in the underlying normal state quasiparticles leave in the (p, 0) region, there is no direct road to the superconducting state (or at least the road is tortuous) since the latter has QP at (p/2, p/2).

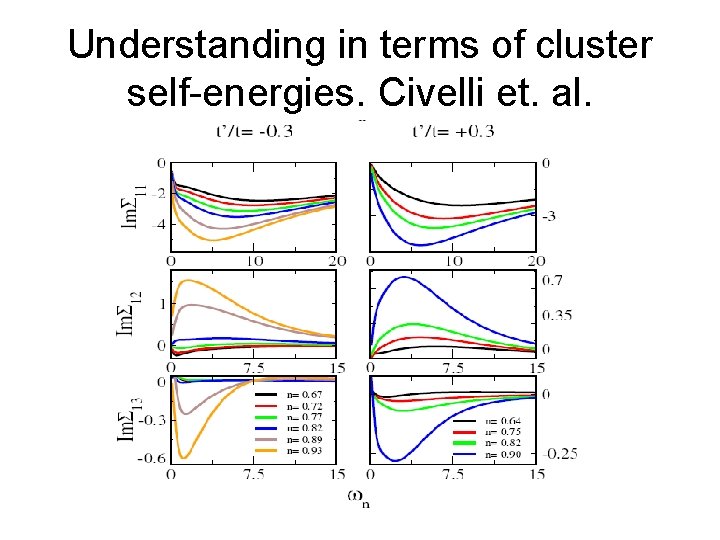
Understanding the result in terms of cluster self energies (eigenvalues)

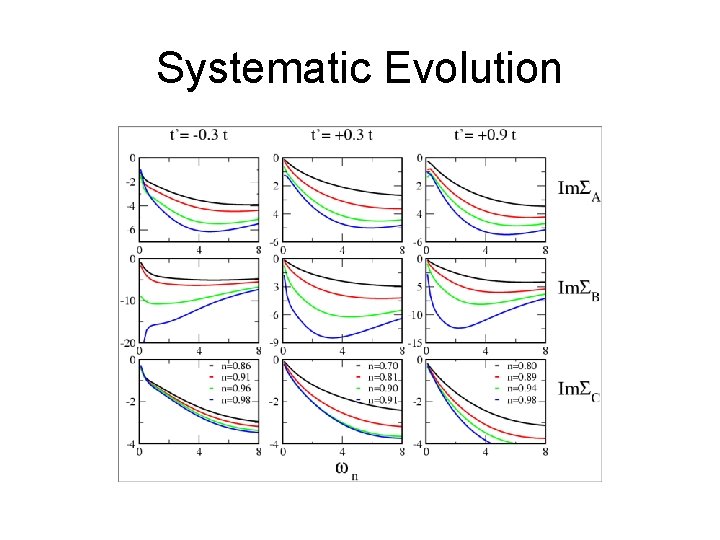
Systematic Evolution

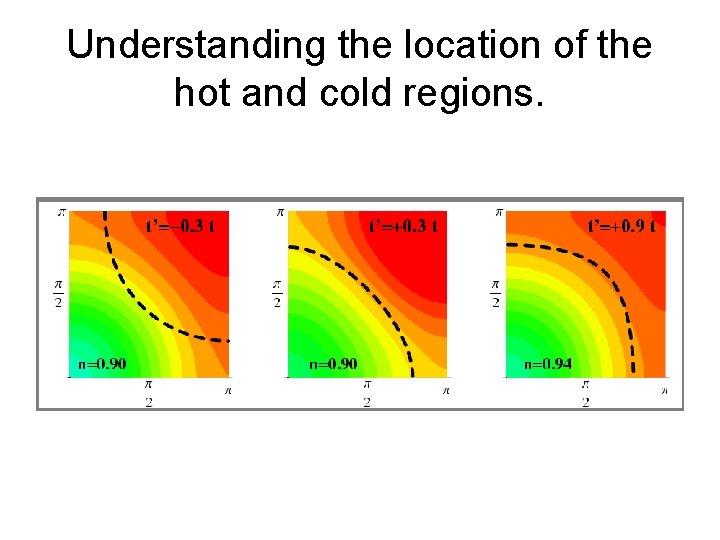
Understanding the location of the hot and cold regions.

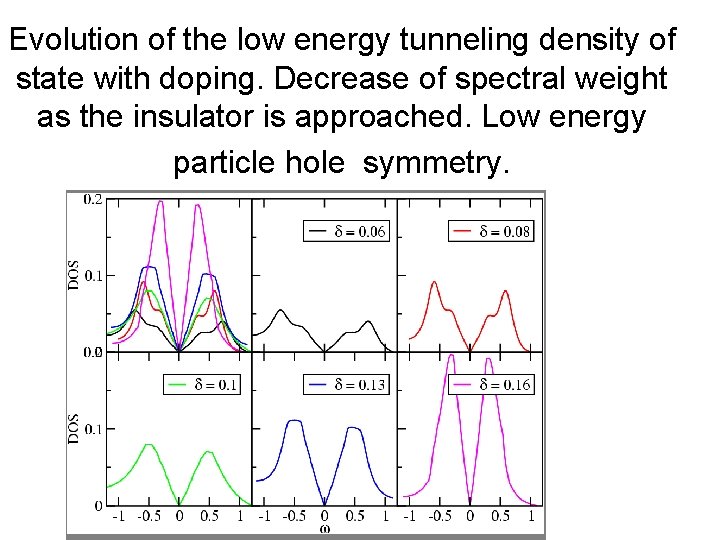
How is the Mott insulator approached from the superconducting state ? Work in collaboration with M. Capone

Evolution of the low energy tunneling density of state with doping. Decrease of spectral weight as the insulator is approached. Low energy particle hole symmetry.

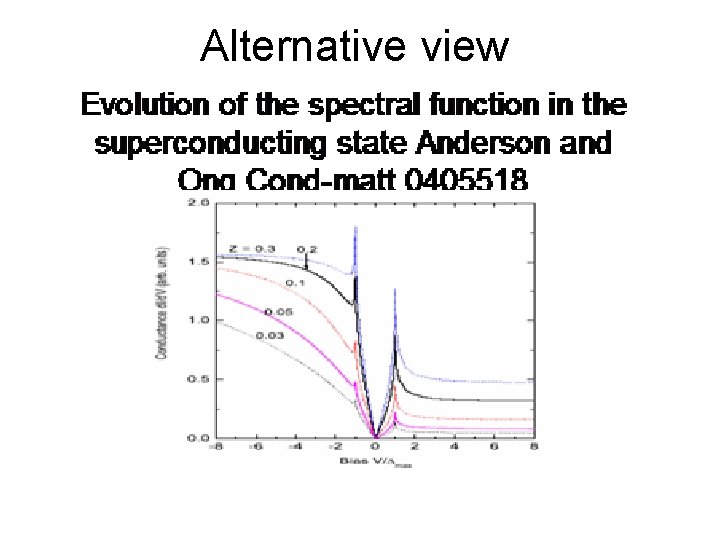
Alternative view

Conclusions • DMFT is a useful mean field tool to study correlated electrons. Provide a zeroth order picture of a physical phenomena. • Provide a link between a simple system (“mean field reference frame”) and the physical system of interest. [Sites, Links, and Plaquettes] • Formulate the problem in terms of local quantities (which we can usually compute better). • Allows to perform quantitative studies and predictions. Focus on the discrepancies between experiments and mean field predictions. • Generate useful language and concepts. Follow mean field states as a function of parameters.

Conclusions • Qualitative effect, momentum space differentiation. Formation of hot –cold regions is an unavoidable consequence of the approach to the Mott insulating state! • General phenomena, but the location of the cold regions depends on parameters. Study the “normal state” of the Hubbard model is useful. • On the hole doped normal and superconducting state can be connected to each other as in the RVB scenario. High Tc superconductivity may result follow from doping a Mott insulator phase but it is not necessarily follow from it. One may not be able to connect the Mott insulator to the superconductor if the nodes are in the “wrong place”.

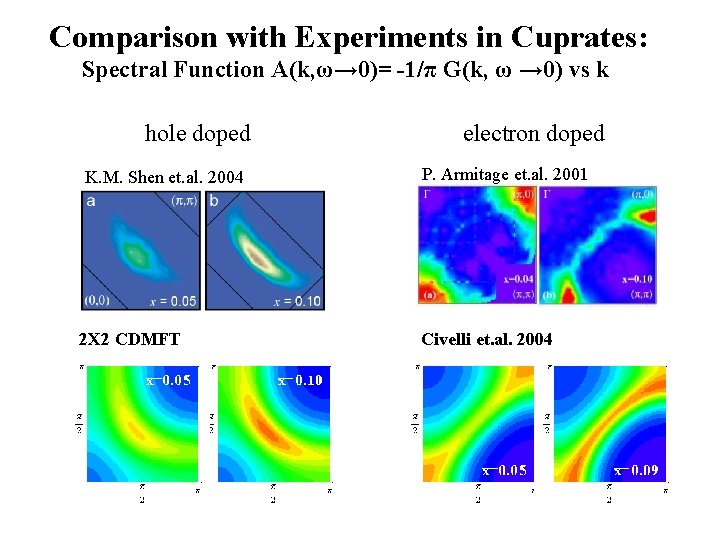
Comparison with Experiments in Cuprates: Spectral Function A(k, ω→ 0)= -1/π G(k, ω → 0) vs k hole doped K. M. Shen et. al. 2004 2 X 2 CDMFT electron doped P. Armitage et. al. 2001 Civelli et. al. 2004

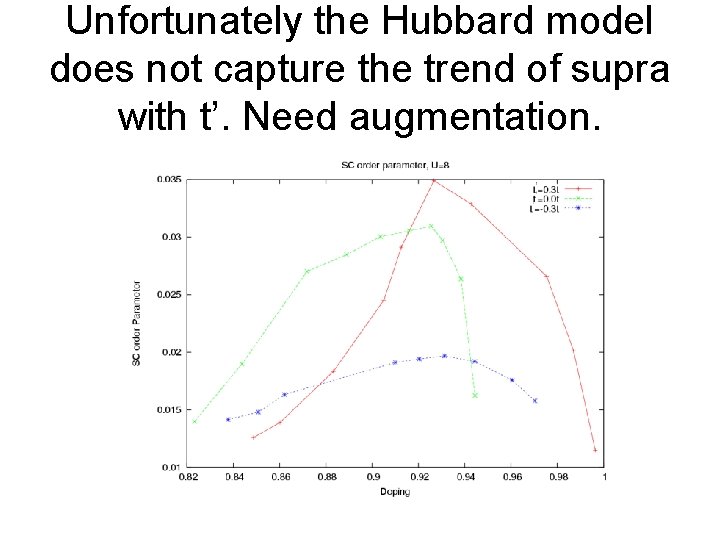
Unfortunately the Hubbard model does not capture the trend of supra with t’. Need augmentation.

CDMFT vs single site DMFT and other cluster methods.

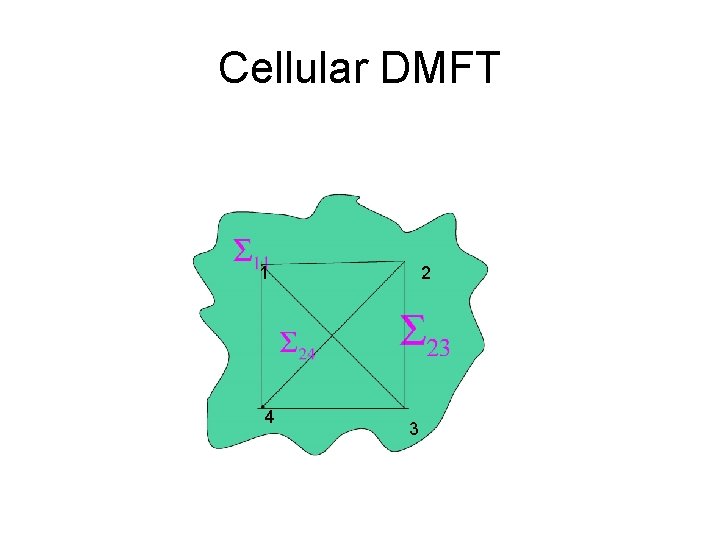
Cellular DMFT 1 4 2 3

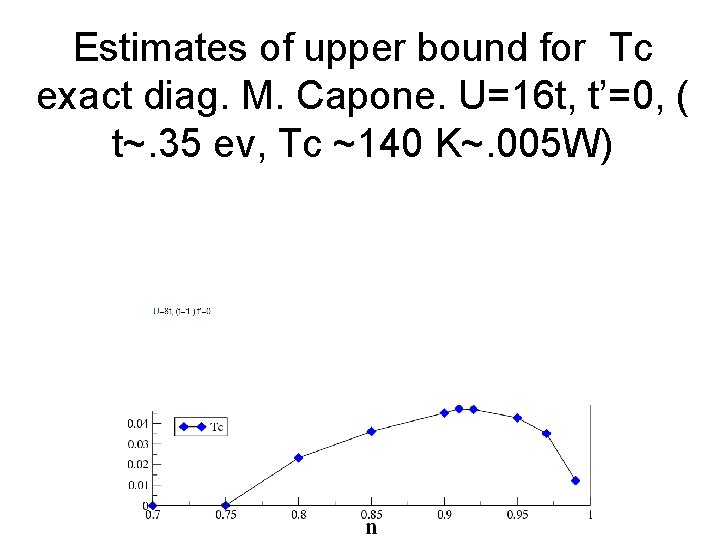
Estimates of upper bound for Tc exact diag. M. Capone. U=16 t, t’=0, ( t~. 35 ev, Tc ~140 K~. 005 W)

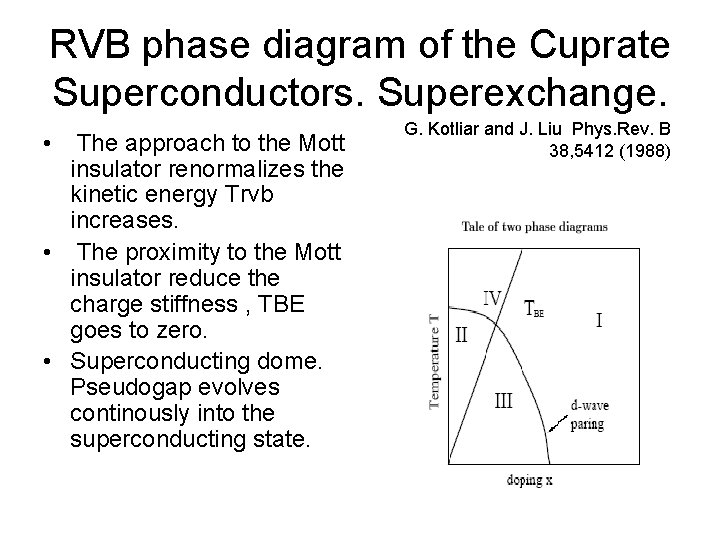
RVB phase diagram of the Cuprate Superconductors • P. W. Anderson. Connection between high Tc and Mott physics. Science 235, 1196 (1987) • Connection between the anomalous normal state of a doped Mott insulator and high Tc. • Baskaran Zhou and Anderson Slave boson approach. <b> coherence order parameter. • k, D singlet formation order parameters.

RVB phase diagram of the Cuprate Superconductors. Superexchange. • The approach to the Mott insulator renormalizes the kinetic energy Trvb increases. • The proximity to the Mott insulator reduce the charge stiffness , TBE goes to zero. • Superconducting dome. Pseudogap evolves continously into the superconducting state. G. Kotliar and J. Liu Phys. Rev. B 38, 5412 (1988)

Problems with the approach. • Numerous other competing states. Dimer phase, box phase , staggered flux phase. Different decouplings, different answers. • Neel order • Stability of the pseudogap state at finite temperature. [Ubbens and Lee] • Missing incoherent spectra. [ fluctuations of slave bosons ] • Temperature dependence of the penetration depth [Wen and Lee , Ioffe and Millis ] • Theory: r[T]=x-Ta x 2 , Exp: r[T]= x-T a. • Mean field is too uniform on the Fermi surface, in contradiction with ARPES.

Site Cellular DMFT. C-DMFT. Kotliar, S. Savrasov, G. Palsson and G. Biroli, Phys. Rev. Lett. 87, 186401 (2001) G. . tˆ(K) hopping expressed in the superlattice notations. • Other cluster extensions (DCA Jarrell Krishnamurthy, M Hettler et. al. Phys. Rev. B 58, 7475 (1998)Katsnelson and Lichtenstein periodized scheme, Nested Cluster Schemes , causality issues, O. Parcollet, G. Biroli and GK Phys. Rev. B 69, 205108 (2004)

Understanding in terms of cluster self-energies. Civelli et. al.

k-(ET)2 X are across Mott transition ET = Insulating anion layer X- Ground State U/t t’/t Cu 2(CN)3 Mott insulator 8. 2 1. 06 Cu[N(CN)2]Cl Mott insulator 7. 5 0. 75 Cu[N(CN)2]Br SC 7. 2 0. 68 Cu(NCS)2 SC 6. 8 0. 84 Cu(CN)[N(CN)2 SC ] Ag(CN)2 H 2 O SC 6. 8 0. 68 6. 6 0. 60 I 3 6. 5 0. 58 X-1 conducting ET layer [(ET)2]+1 modeled to triangular lattice t’ t SC

Electron doped case t’=. 9 t U=16 t n=. 69. 92. 96 Color scale x=. 9, . 32, . 22

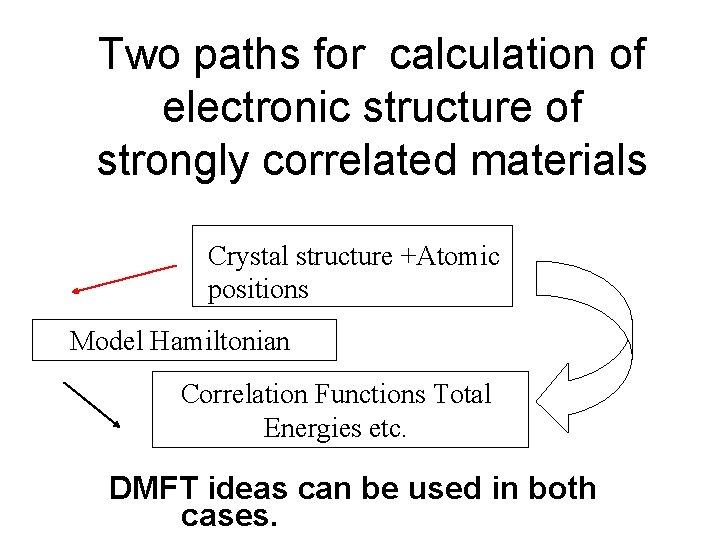
Two paths for calculation of electronic structure of strongly correlated materials Crystal structure +Atomic positions Model Hamiltonian Correlation Functions Total Energies etc. DMFT ideas can be used in both cases.