Cluster Analysis University of Houston Computer Science Prof

Cluster Analysis University of Houston – Computer Science Prof. Huang Chris De. Vito 2/1/2013

Outline • Cluster Analysis • Center Closeness Algorithm • Performance • Issues

Cluster Analysis • Improved Algorithm for the Analyses of Gaussian Data: homogeneity criterion • Hierarchal Clustering Algorithms: k-means • Initial cluster center points • When to terminate loop • Applications: Network Intrusion, cancer detection

Gaussian Data

A Center Closeness Algorithm: Analysis of Gene Expression Data by Huakun Wang, Lixin Feng, Zhou Ying, Zhang Xu • Problem: clustering high dimension data, Prostate tumor data(cancer) and BRAIN-MD (brain tumor data), from MIT. Overcome k-means problems of determining cluster aprioi, instead develop new method , Center-closeness clustering algorithm (CLC). • Assumptions: Assume minimum 2 clusters with maximum N clusters, and n data points. • Concept: CLC based that data points with similar characteristics must have individual attributes close in value of distance measure. • Definition: closeness=dist. (x, y) = || x – y || where x, y are points with n-dimensions

Center Closeness Algorithm 1. From the set of data points, choose any one to be the first center (C 1), 2. Find point farthest from this center, and make it the second center(C 2), 3. Assign remaining points to closest center, 4. Create another cluster? a. Calculate R = distance(C 1 -C 2)/2. b. Calculate the distance (D) from each point to its center. If D>R, create third center. 5. To find the third center, find the point which is the farthest from its center (1 or 2). 6. Assign points to closest center, 7. Calculate R = 8. While D>R create new cluster, until all points are within R units of their center.

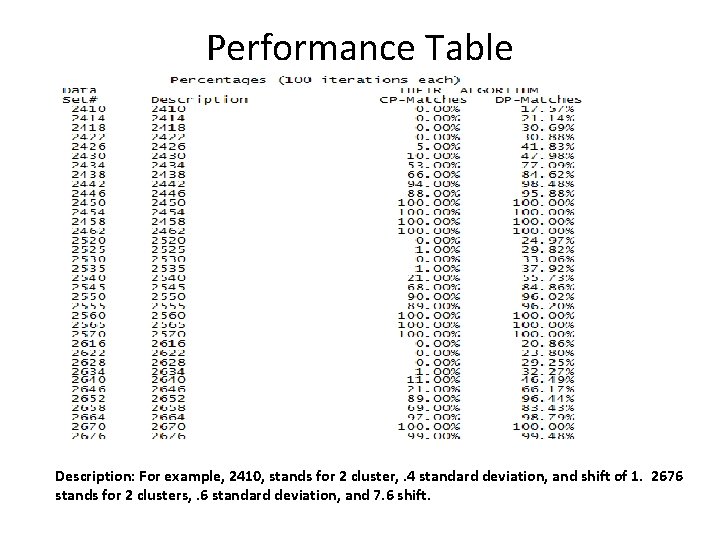
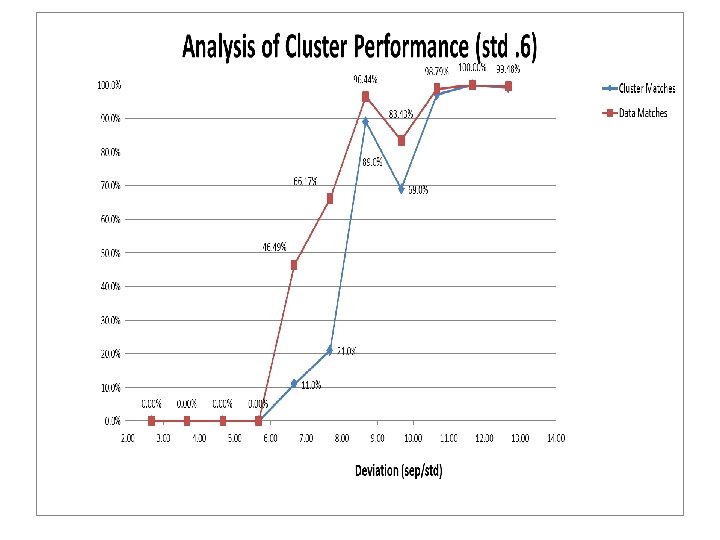
Performance Table Description: For example, 2410, stands for 2 cluster, . 4 standard deviation, and shift of 1. 2676 stands for 2 clusters, . 6 standard deviation, and 7. 6 shift.

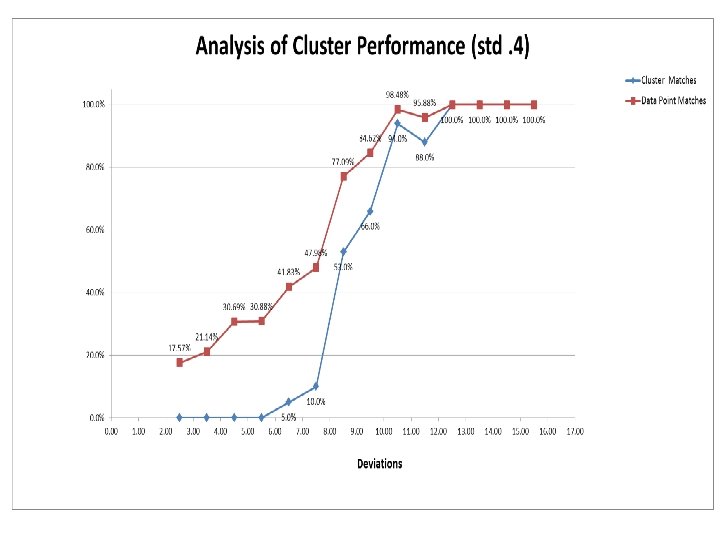
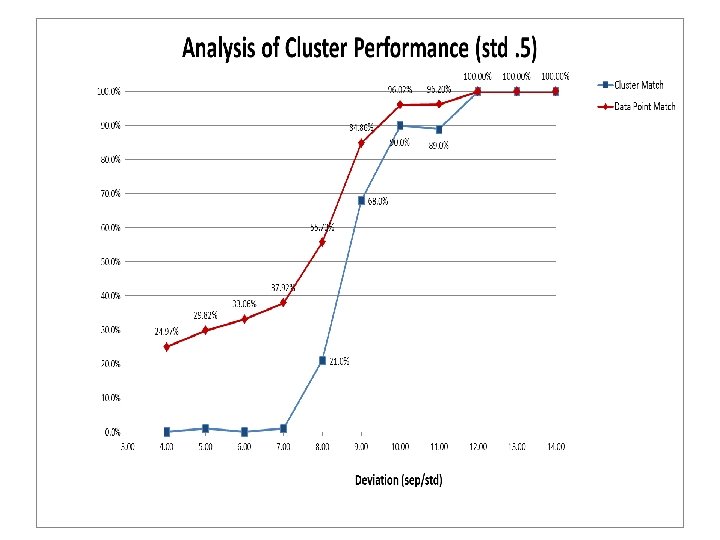
Performance • General Rise in performance in both Data point and Cluster matches • The. 4 std better performance was not realized until 10 deviations, whereas. 5 and. 6 was realized earlier at 8 -9 deviation range • After a sharp rise in performance, there was a slight decrease in performance, then slow plateauing to optimum at 12 deviations.

Issues 1) Determining Number of Clusters with small intra cluster separation D>R where D is inter and R is intra so with small R, algorithm will over cluster. 2) Initial Center points: Centers are rigid and fixed once assigned and affects performance. Solution? Look into adjusting centers (real or imaginary). 3) Euclidian Distance? Look into additional measurements, for example instead of focusing on centers only, create a feature vector of a summary of the cluster itself (i. e. covariance of n dimensions of m points in cluster). Or create a membership function based on density of points within cluster, or vector.

Issues 3) Weighted average, sort of like membership function by taking a weight, but possibly looking at taking the weight of dimensions. 4) Similarity Function: With Euclidian distance we define similarity as inter versus intra distances. Adjust definition of similarity between the combinations of every pair of points within each cluster, then average result of similarity over values between all points in all cluster. 5) Data: Center closeness seems to work well on 3 d normal gaussian data, would like to test on iris (4 d) and later use medical data.