Clouds and Large Model Grid Boxes Damian Wilson

Clouds and Large Model Grid Boxes Damian Wilson Atmospheric Processes and Parametrization Met Office With help from: Andrew Bushell, Jeremy Price, Keith Williams, Rob Wood, Paul Field, Olaf Stiller 1

Contents 2 n What is a cloud…? n Why do we need to represent clouds in a model? n What do we need to know about them? n How can we estimate these quantities? n How effective are current methods? n How can we do better? n What have we learnt?

Contents 3 n What is a cloud…? n Why do we need to represent clouds in a model? n What do we need to know about them? n How can we estimate these quantities? n How effective are current methods? n How can we do better? n What have we learnt?

Contents 4 n What is a cloud…? n Why do we need to represent clouds in a model? n What do we need to know about them? n How can we estimate these quantities? n How effective are current methods? n How can we do better? n What have we learnt?

Clouds in the atmosphere Clouds have several effects in the atmosphere: Radiative transfer Latent heat Moisture transport Chemistry Visibility To fully calculate the effect of each we would need to know the full three dimensional distribution of liquid and ice contents. 5

Radiative importance of clouds 12 Z 10/1/03 2152 Z 18 Z 6 -6 to -4 -4 to -2 -2 to 0 18 Z

Contents 7 n What is a cloud…? n Why do we need to represent clouds in a model? n What do we need to know about them? n How can we estimate these quantities? n How effective are current methods? n How can we do better? n What have we learnt?

A basic cloud representation 8 n On the very small scale, we can represent clouds by growing particles (e. g. Köhler theory). n On the slightly larger scale we might assume that condensational growth or evaporation is fast enough to maintain the surroundings at saturation. n This assumption isn’t good enough for ice, so we must use a distribution of particles and integrate the depositional growth equation. n And. . .

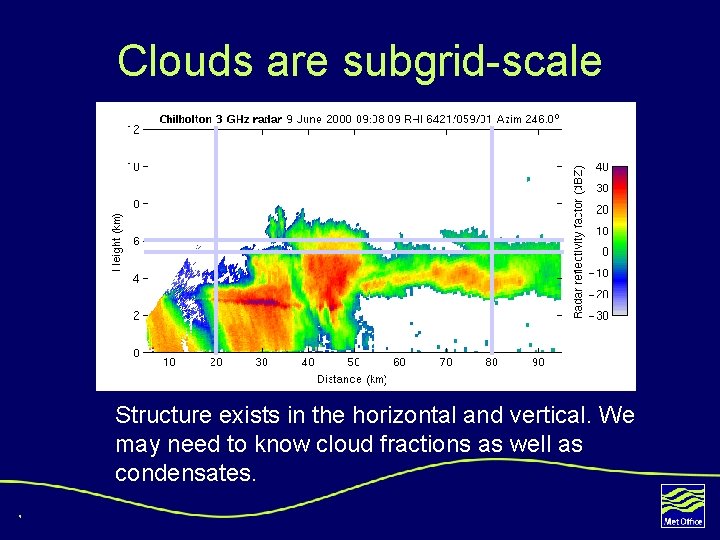
Clouds are subgrid-scale Structure exists in the horizontal and vertical. We may need to know cloud fractions as well as condensates. 9

Is subgrid-scale cloud information important? 10 n Some simple theory n Some simulations

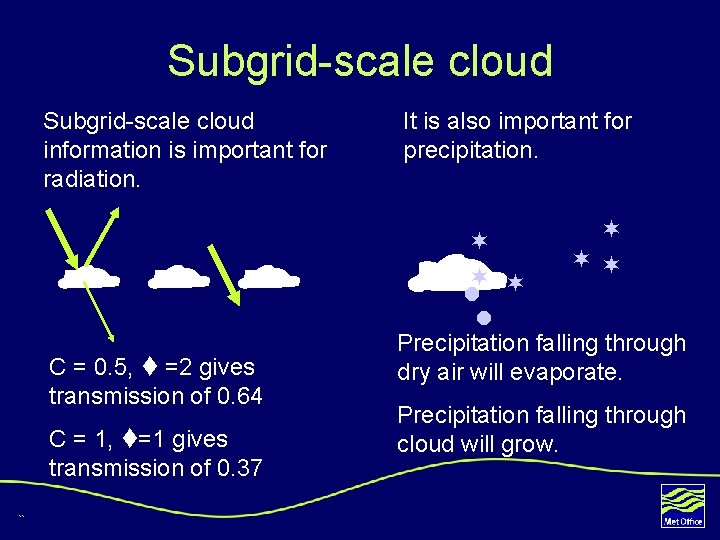
Subgrid-scale cloud information is important for radiation. C = 0. 5, =2 gives transmission of 0. 64 C = 1, =1 gives transmission of 0. 37 11 It is also important for precipitation. Precipitation falling through dry air will evaporate. Precipitation falling through cloud will grow.

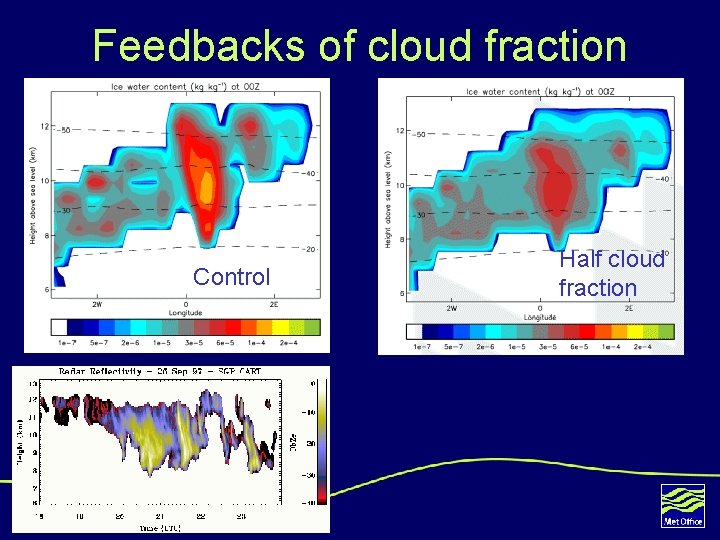
Feedbacks of cloud fraction Control 12 Half cloud fraction

What do we need to know about clouds? 13 n Cloud fraction n Cloud thickness - how much condensate is present n Cloud morphology n Particle phase and size distributions

Contents 14 n What is a cloud…? n Why do we need to represent clouds in a model? n What do we need to know about them? n How can we estimate these quantities? n How effective are current methods? n How can we do better? n What have we learnt?

Instantaneous condensation q. T>qsat Cloudy q. T=qsat(T) condensate q. T<qsat Clear T Consider as a 1 D distribution of q. T - qsat 15

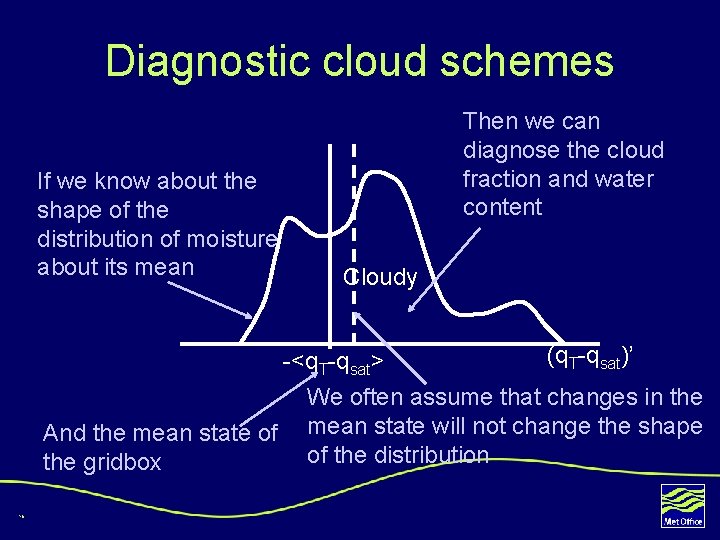
Diagnostic cloud schemes If we know about the shape of the distribution of moisture about its mean Then we can diagnose the cloud fraction and water content Cloudy (q. T-qsat)’ -<q. T-qsat> We often assume that changes in the And the mean state of mean state will not change the shape of the distribution the gridbox 16

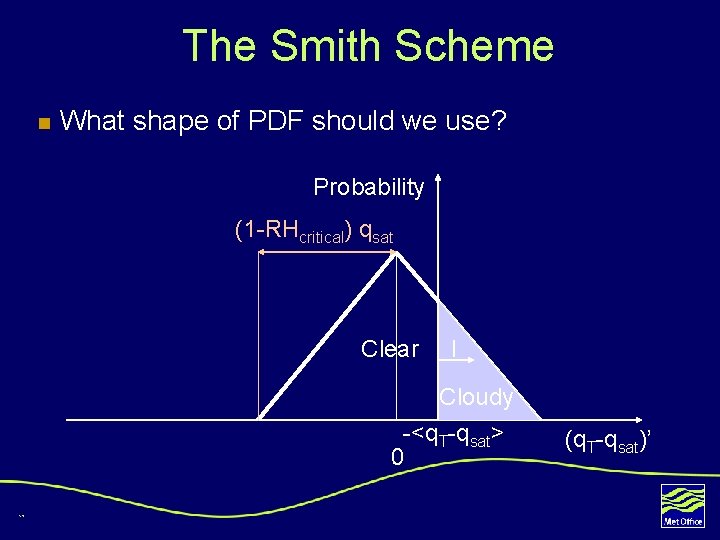
The Smith Scheme n What shape of PDF should we use? Probability (1 -RHcritical) qsat Clear l Cloudy -<q. T-qsat> 0 17 (q. T-qsat)’

Contents 18 n What is a cloud…? n Why do we need to represent clouds in a model? n What do we need to know about them? n How can we estimate these quantities? n How effective are current methods? n How can we do better? n What have we learnt?

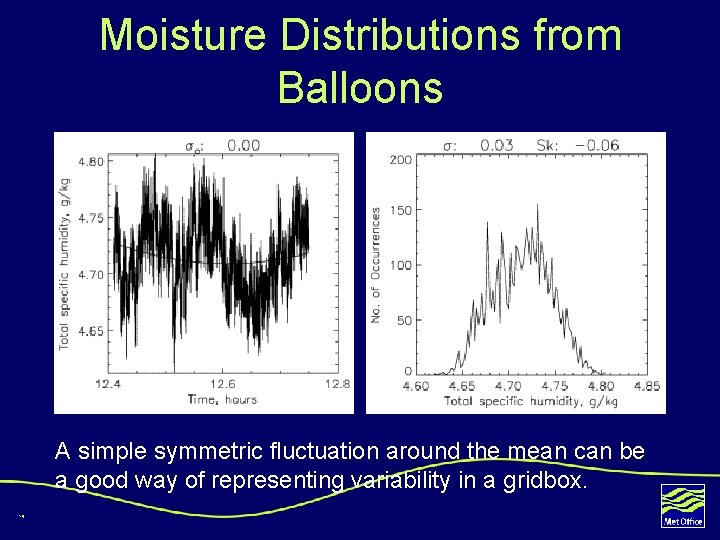
Moisture Distributions from Balloons A simple symmetric fluctuation around the mean can be a good way of representing variability in a gridbox. 19

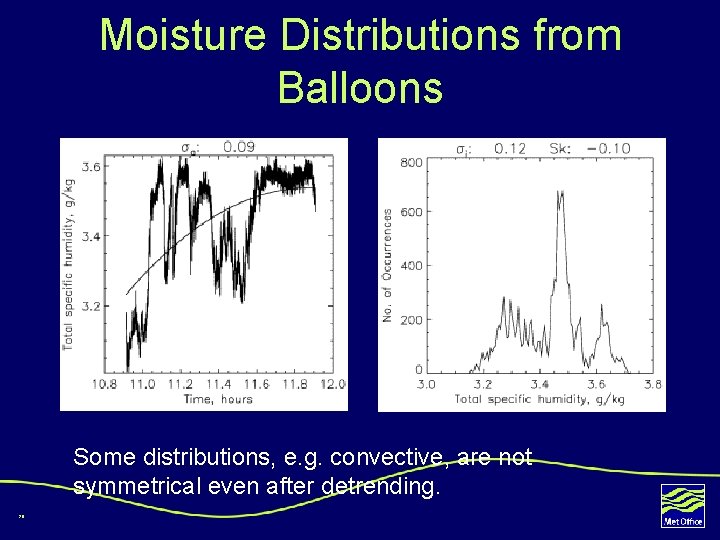
Moisture Distributions from Balloons Some distributions, e. g. convective, are not symmetrical even after detrending. 20

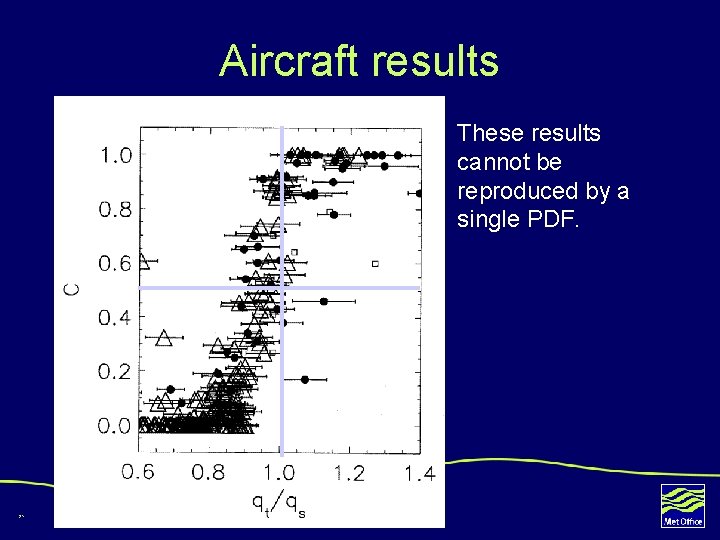
Aircraft results These results cannot be reproduced by a single PDF. 21

Do these inaccuracies matter? 22 n Forecasts n Climate predictions

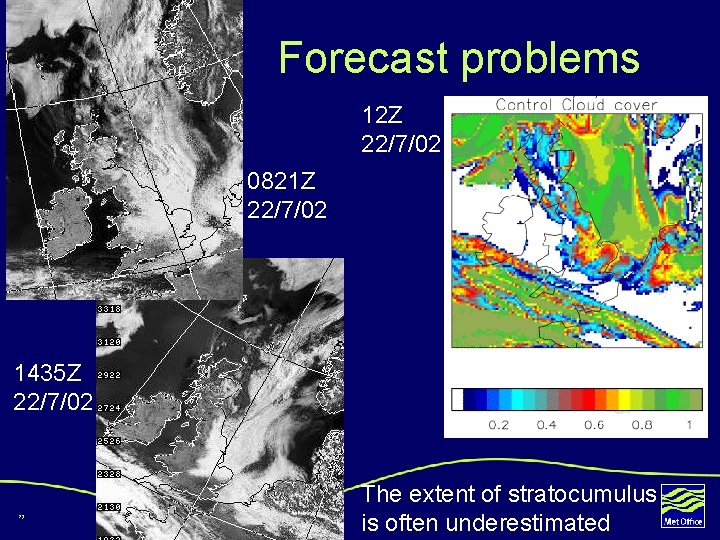
Forecast problems 12 Z 22/7/02 0821 Z 22/7/02 1435 Z 22/7/02 23 The extent of stratocumulus is often underestimated

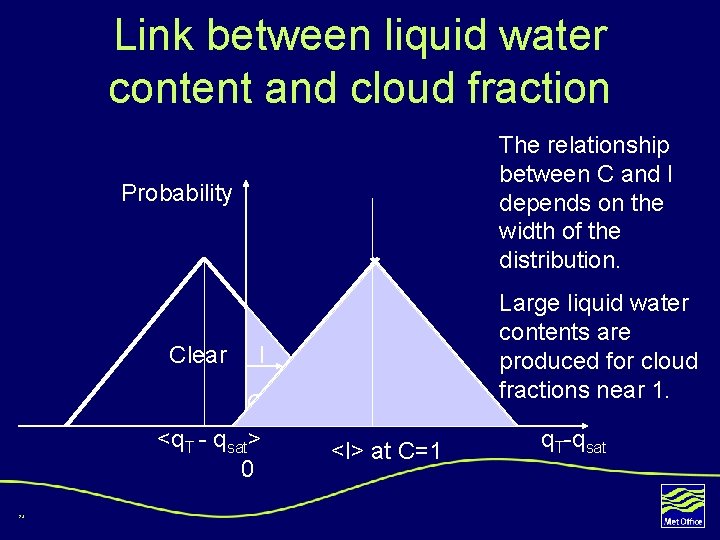
Link between liquid water content and cloud fraction The relationship between C and l depends on the width of the distribution. Probability Clear l Cloudy <q. T - qsat> <l> at C=1 0 24 Large liquid water contents are produced for cloud fractions near 1. q. T-qsat

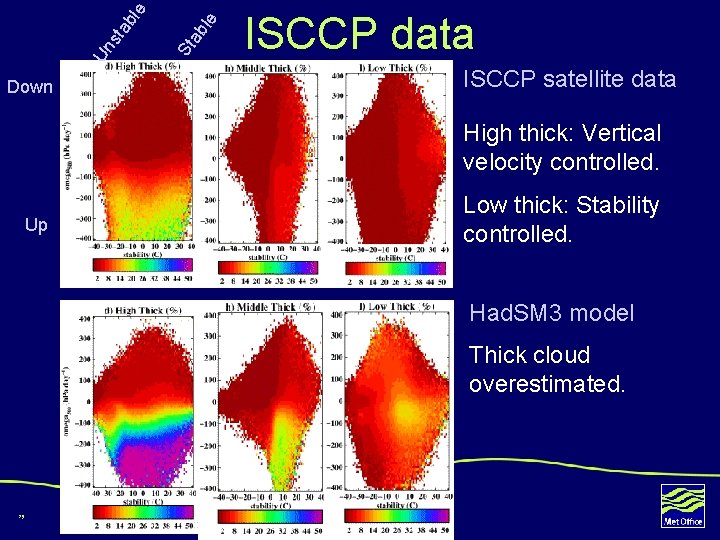
le ab St ble Un sta Down ISCCP data ISCCP satellite data High thick: Vertical velocity controlled. Up Low thick: Stability controlled. Had. SM 3 model Thick cloud overestimated. 25

Contents 26 n What is a cloud…? n Why do we need to represent clouds in a model? n What do we need to know about them? n How can we estimate these quantities? n How effective are current methods? n How can we do better? n What have we learnt?

Building a prognostic scheme n We choose specify the sources and sinks of – Liquid condensate – Ice condensate – Liquid cloud fraction – Ice cloud fraction – Total cloud fraction 27 n For all processes which occur in the model n We can use Cloud resolving models, observations and conceptual models to help.

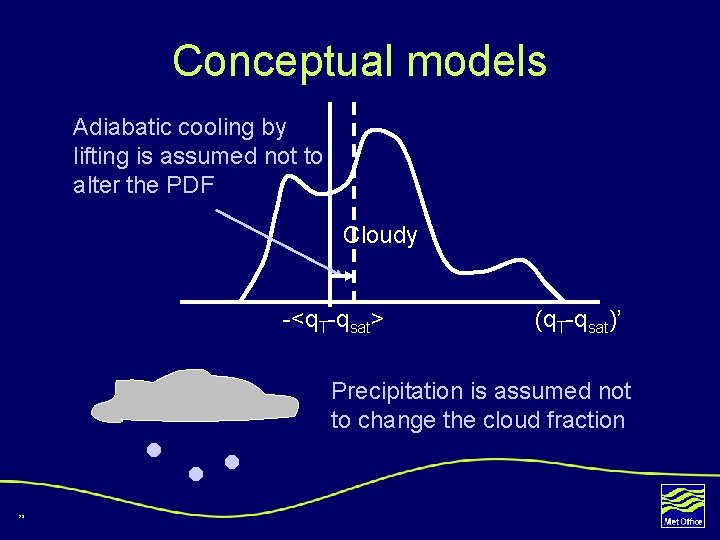
Conceptual models Adiabatic cooling by lifting is assumed not to alter the PDF Cloudy -<q. T-qsat> (q. T-qsat)’ Precipitation is assumed not to change the cloud fraction 28

Does a prognostic scheme do any better? 29 n Forecast results n Microphysical comparison

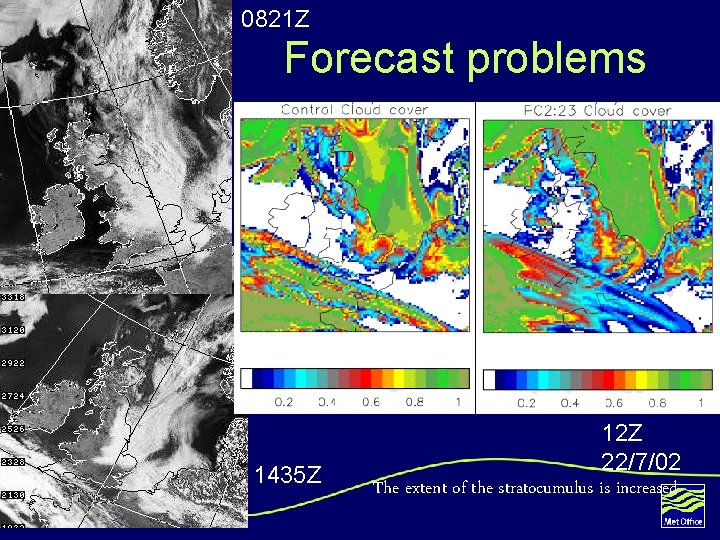
0821 Z Forecast problems 1435 Z 30 12 Z 22/7/02 The extent of the stratocumulus is increased

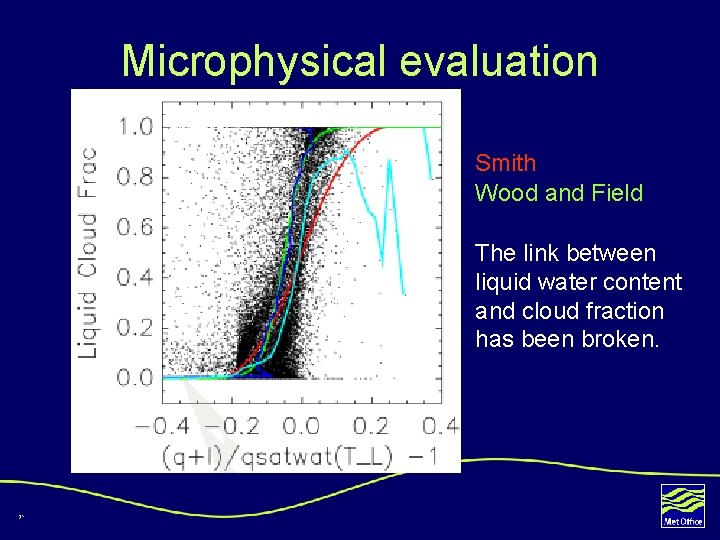
Microphysical evaluation Smith Wood and Field The link between liquid water content and cloud fraction has been broken. 31

Contents 32 n What is a cloud…? n Why do we need to represent clouds in a model? n What do we need to know about them? n How can we estimate these quantities? n How effective are current methods? n How can we do better? n What have we learnt?

Summary n Clouds have a large effect on radiative transfer, hence surface temperatures and circulation. n Clouds are usually below the size of model grid-boxes. n Symmetric probability density function parametrizations are good in many cases (for liquid cloud) but have problems. n Prognostic cloud schemes allow a more direct link between processes and clouds. n Modelled climate feedbacks and weather forecasts depend strongly on how sub-grid clouds are represented. 33

34

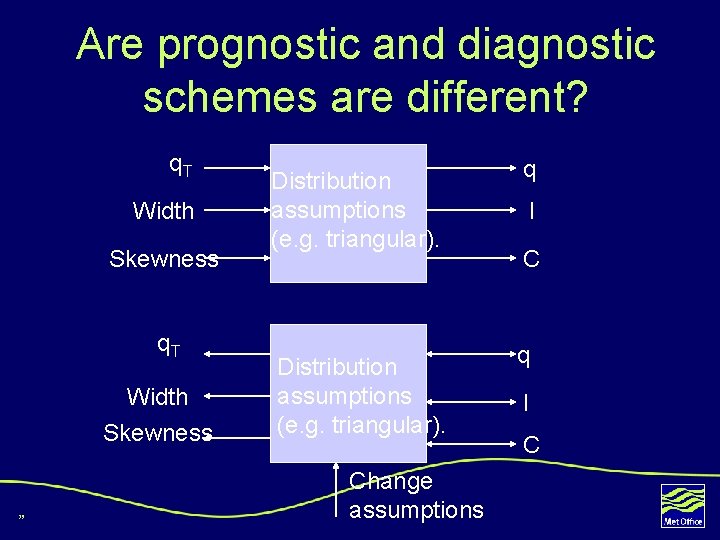
Are prognostic and diagnostic schemes are different? q. T Width Skewness 35 Distribution assumptions (e. g. triangular). q Change assumptions l C

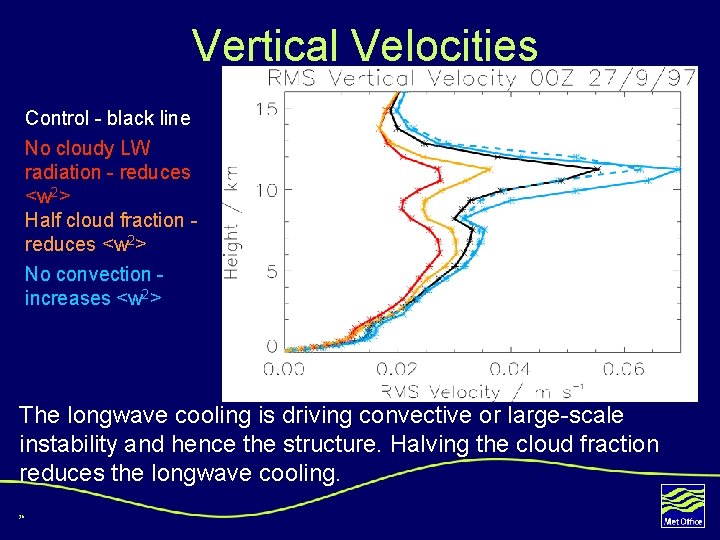
Vertical Velocities Control - black line No cloudy LW radiation - reduces <w 2> Half cloud fraction reduces <w 2> No convection increases <w 2> The longwave cooling is driving convective or large-scale instability and hence the structure. Halving the cloud fraction reduces the longwave cooling. 36

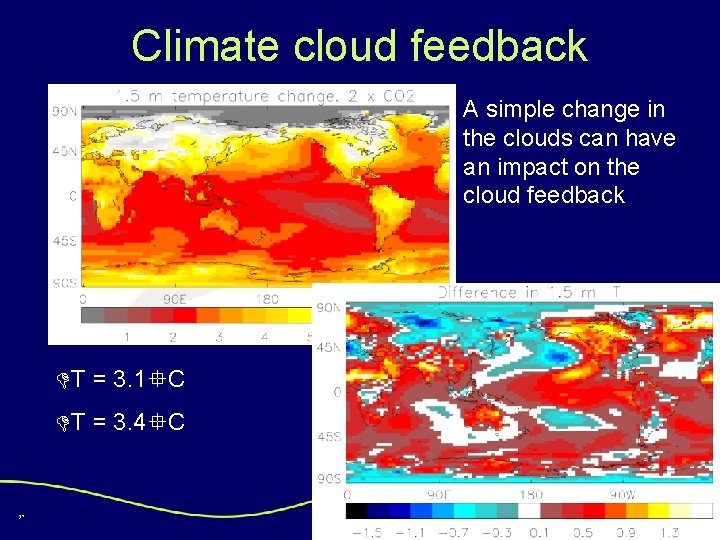
Climate cloud feedback A simple change in the clouds can have an impact on the cloud feedback T = 3. 1 C T = 3. 4 C 37

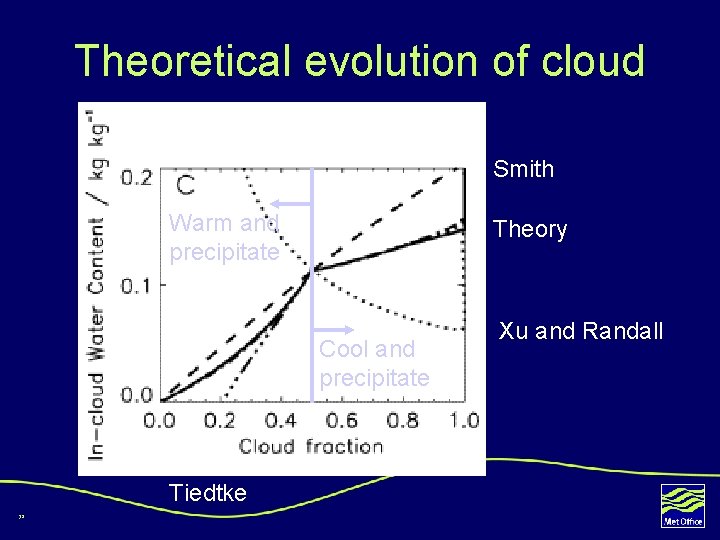
Theoretical evolution of cloud Smith Warm and precipitate Theory Cool and precipitate Tiedtke 38 Xu and Randall

Ice cloud Nucleation Liquid saturation Ice super-saturation Fall of ice Sublimation 39 The assumption of instantaneous condensation for ice cloud is not good. It excludes the possibility of supercooled liquid cloud.

Clouds 40 A cloud droplet will grow and shrink by diffusion of water vapour molecules to and from the surface until a dynamic equilibrium is reached with the surroundings.

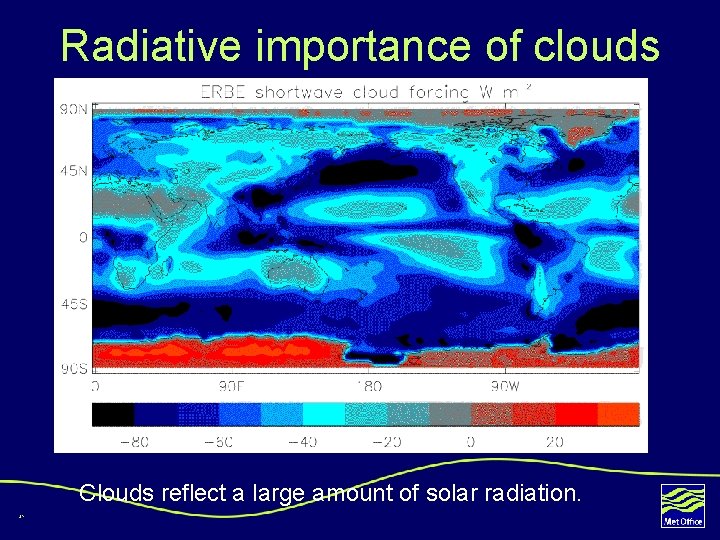
Radiative importance of clouds Clouds reflect a large amount of solar radiation. 41

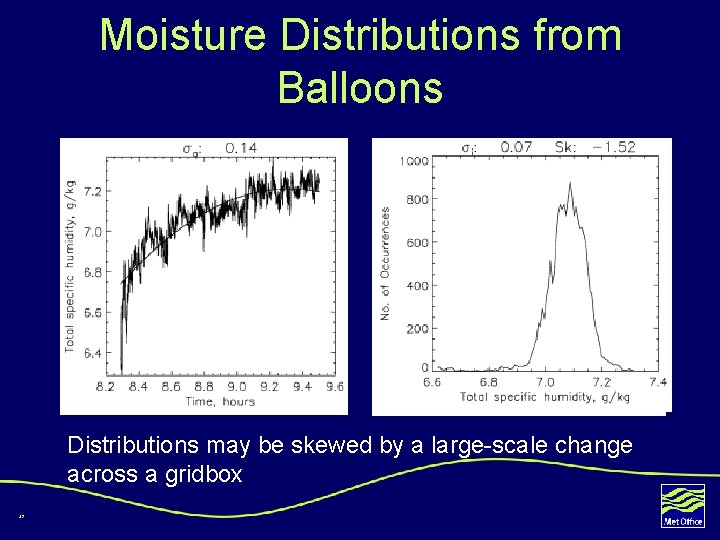
Moisture Distributions from Balloons Distributions may be skewed by a large-scale change across a gridbox 42

A prognositic scheme? Anvils detrained from convective cores can exist long after the convection has died down. 43

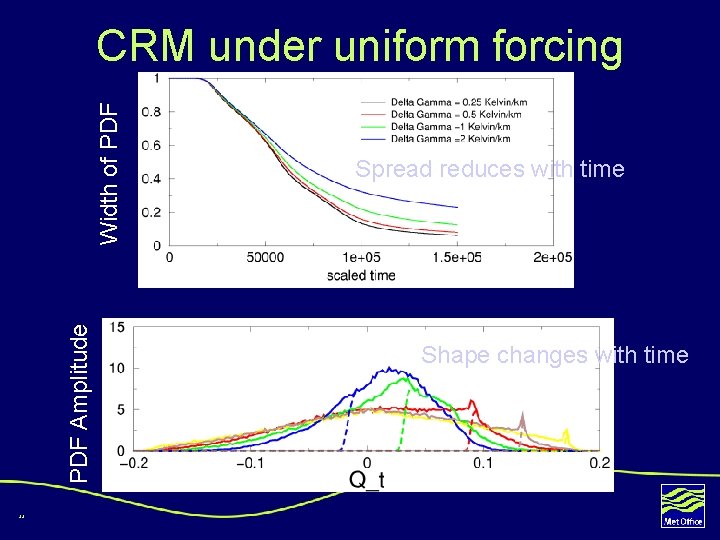
PDF Amplitude Width of PDF CRM under uniform forcing 44 Spread reduces with time Shape changes with time