Cloud Fragmentation via filament formation Tsuribe T Osaka

Cloud Fragmentation via filament formation Tsuribe, T. (Osaka U. ) Contents: Introduction Basic Aspects of Cloud Fragmentation Application to the Metal deficient Star Formation based on Omukai, TT, Schineider, Ferrara 2005, Ap. J TT&Omukai 2006, Ap. JL TT&Omukai 2008, Ap. JL (+if possible, some new preliminary results) 2009/01/14 -16 @Tsukuba

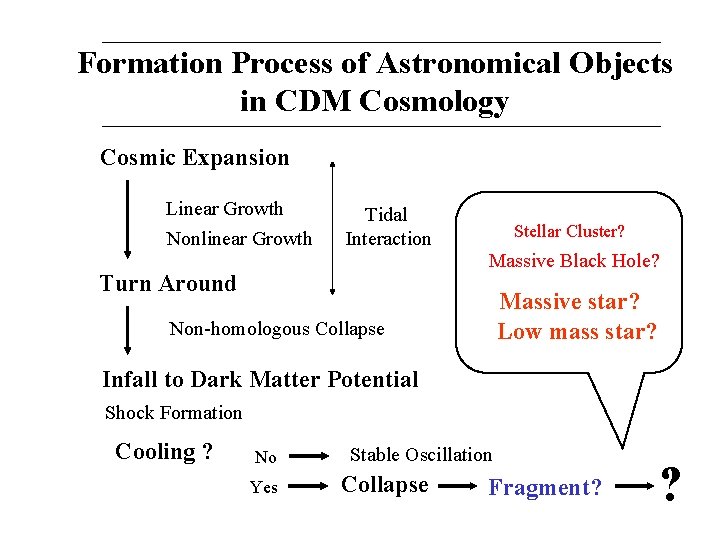
Formation Process of Astronomical Objects in CDM Cosmology Cosmic Expansion Linear Growth Nonlinear Growth Tidal Interaction Turn Around Stellar Cluster? Massive Black Hole? Massive star? Low mass star? Non-homologous Collapse Infall to Dark Matter Potential Shock Formation Cooling ? No Yes Stable Oscillation Collapse Fragment? ?

Possibility of Subfragmentation? Density Fluctuations Cloud Core ? Fragmentation When fragmentation stops? Fragments Simple criterion? Runaway Collapse Core Formation Accretion ／ Merging Stars Feedback …UV, SNe, etc.

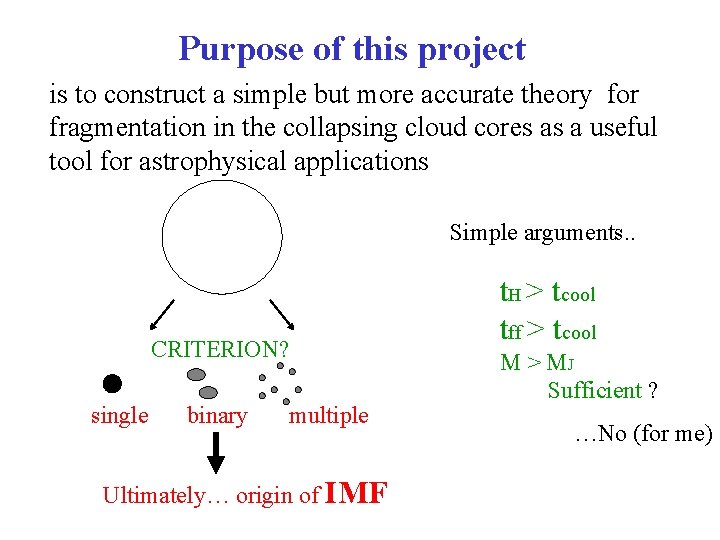
Purpose of this project is to construct a simple but more accurate theory for fragmentation in the collapsing cloud cores as a useful tool for astrophysical applications Simple arguments. . CRITERION? single binary multiple Ultimately… origin of IMF t. H > tcool tff > tcool M > MJ Sufficient ? …No (for me)

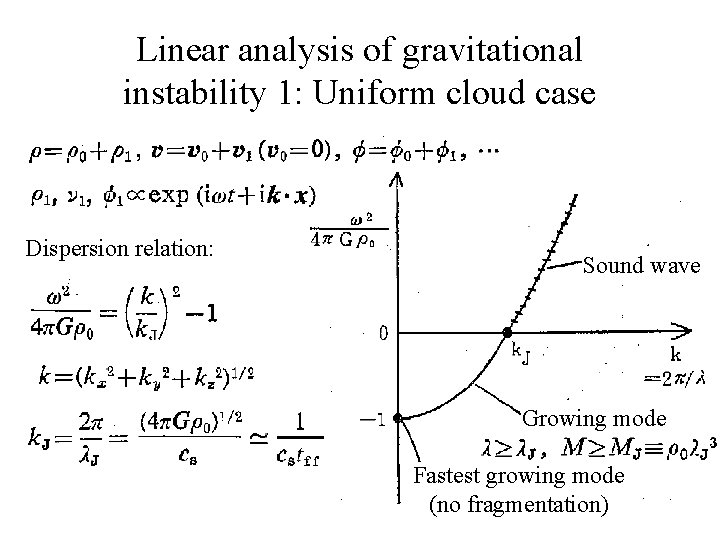
Linear analysis of gravitational instability 1: Uniform cloud case Dispersion relation: Sound wave Growing mode Fastest growing mode (no fragmentation)

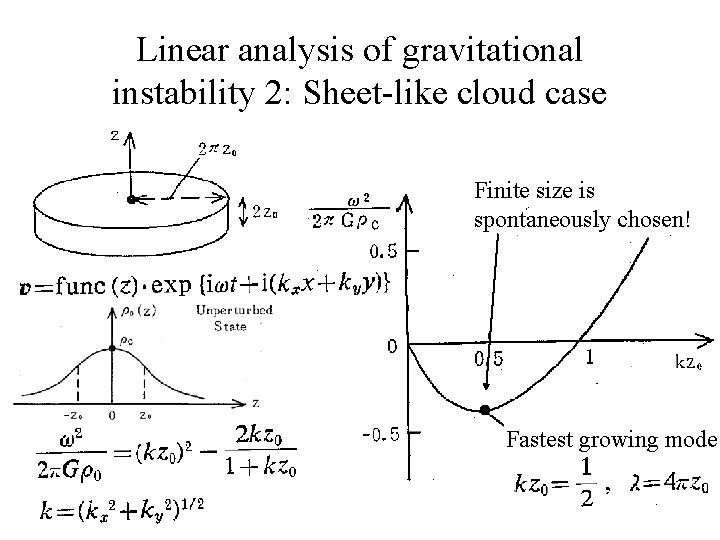
Linear analysis of gravitational instability 2: Sheet-like cloud case Finite size is spontaneously chosen! Fastest growing mode

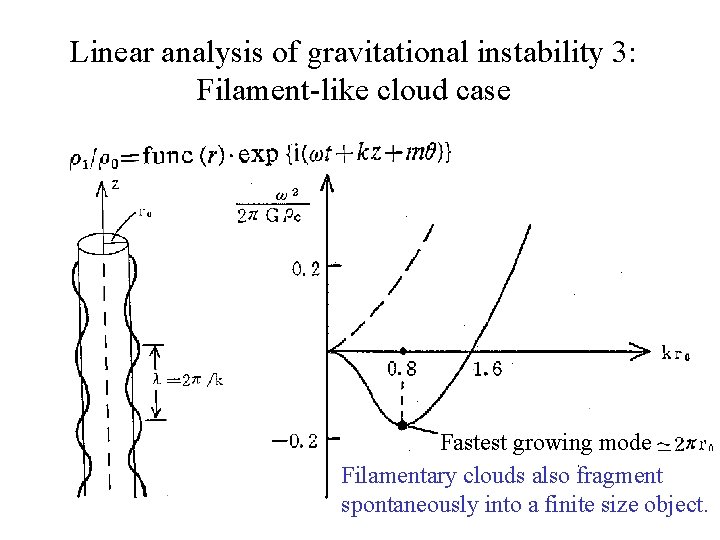
Linear analysis of gravitational instability 3: Filament-like cloud case Fastest growing mode Filamentary clouds also fragment spontaneously into a finite size object.

In this talk, in order to understand the possibility of (sub)fragmentation of self-gravitating run-away collapsing cloud core, Physical property of non-spherical gravitational collapse is a key. Collapsing cloud core Elongation & Filament Formation? Fragmentation? … this talk Disk formation? Ring formation? c. f. , Omukai-san’s talk

In primordial star formation, infinite length filament is investigated by e. g. , Uehara, Susa, Nishi, Yamada&Nakamura(1996) Uehara&Inutsuka(2000) Nakamura&Umemura (1999, 2001, 2002) Isothermal G P density In a infinite length filament, since With increasing T P Fg = GM/R … R^-1 G Fp = cs^2 rho/R … R^-1 (for isothermal), density isothermal evolution has a special meaning. … Break down of isothermality is sometimes interpreted as a site of fragmentation In this work, the formation process of filament from the finite size core is also investigated.

Elongation of cloud core If non-spherical perturbation is given to a spherical fragment … Elongation Unstable It will elongate to form sheet or filament Possibly fragment again Stable It keeps spherical shape It will form massive object without fragmentation Condition of elongation instability? Condition for fragmentation?

Non-spherical elongation of a self-similar collapse solution Hanawa&Matsumoto (2000) Lai (2001) Zooming coordinate Equations in self-similar frame

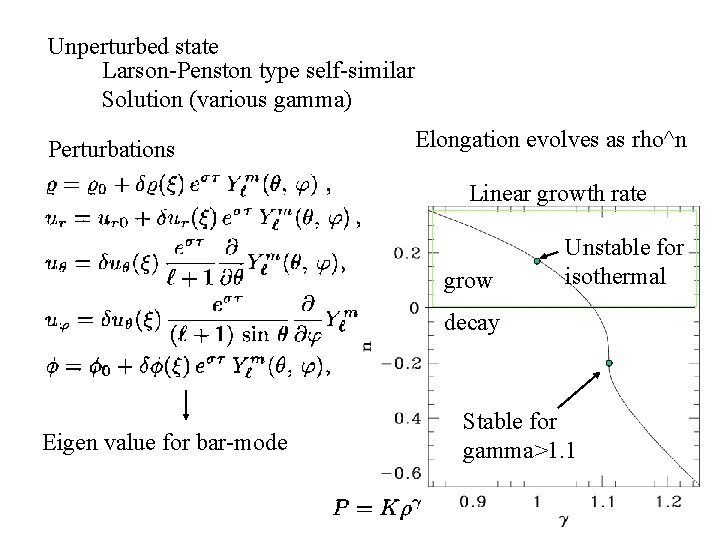
Unperturbed state Larson-Penston type self-similar Solution (various gamma) Perturbations Elongation evolves as rho^n Linear growth rate grow Unstable for isothermal decay Eigen value for bar-mode Stable for gamma>1. 1

Effect of the dust cooling for elongation

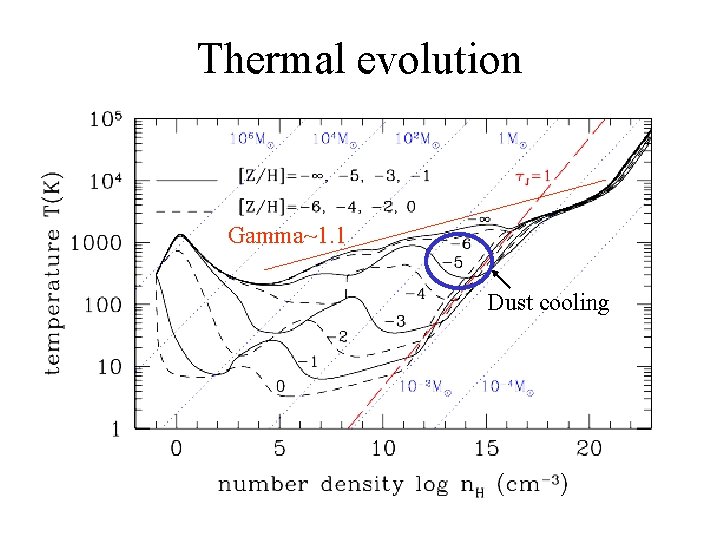
Thermal evolution Gamma~1. 1 Dust cooling

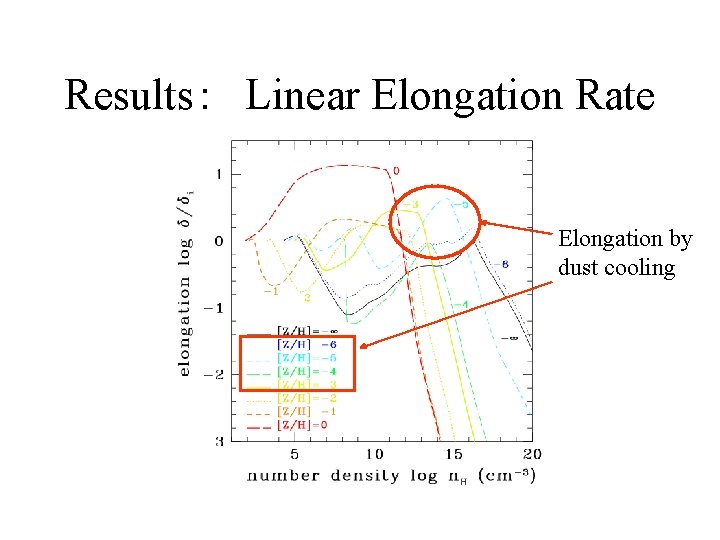
Results： Linear Elongation Rate Elongation by dust cooling

Fragmentation Sites (by linear growth + thresholds + Monte Carlro) mass function Fragmentation

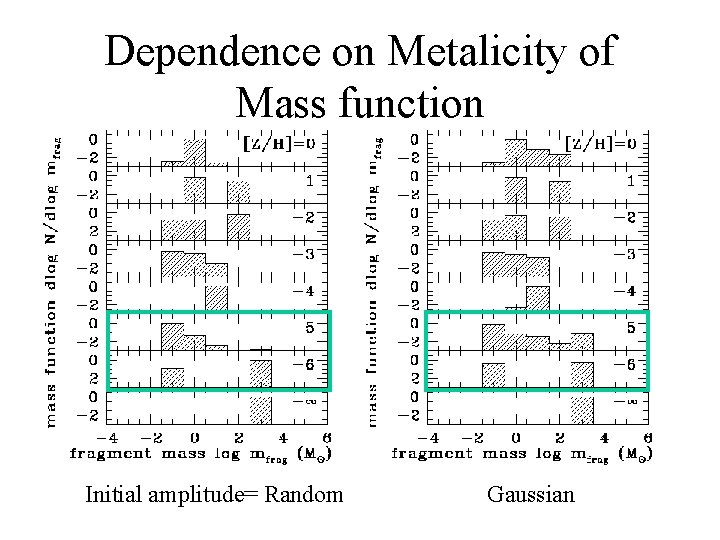
Dependence on Metalicity of Mass function Initial amplitude= Random Gaussian

Fragmentation Sites (by linear growth + thresholds + Monte Carlro) Solved range Fragmentation

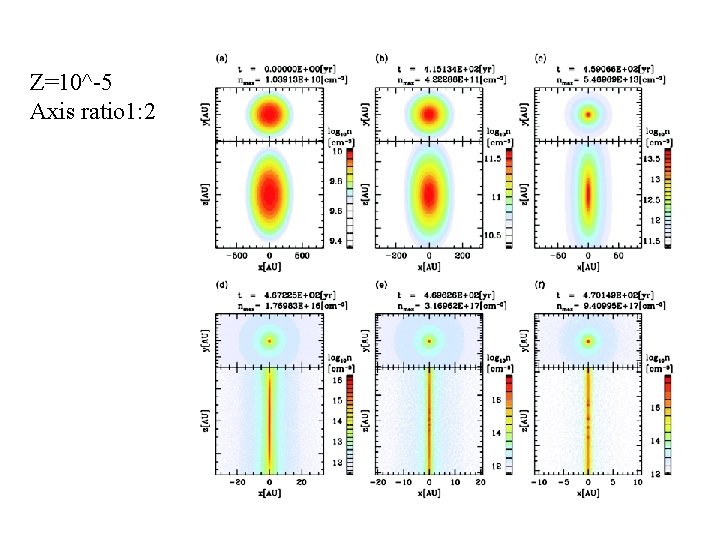
Z=10^-5 Axis ratio 1: 2

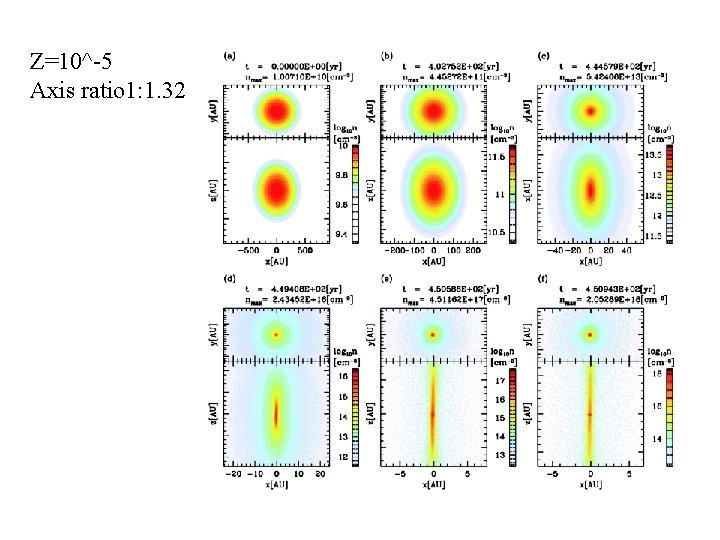
Z=10^-5 Axis ratio 1: 1. 32

Effect of Sudden heating + Dust cooling

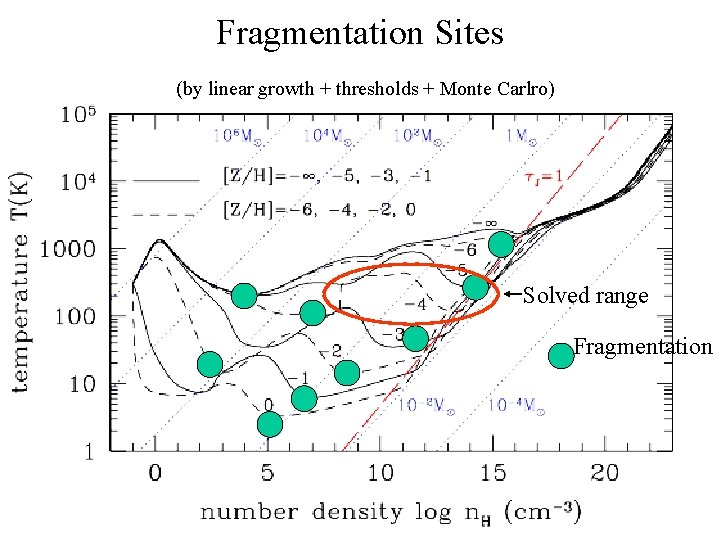
Fragmentation Sites (by linear growth + thresholds + Monte Carlro) Solved range Fragmentation

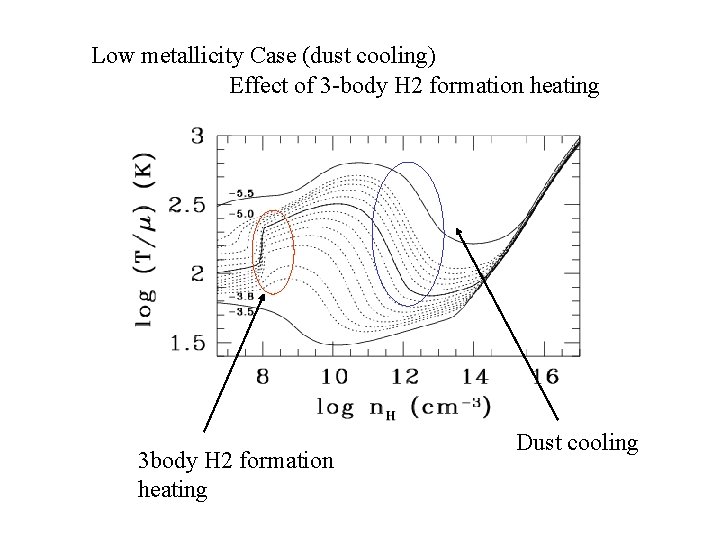
Low metallicity Case (dust cooling) Effect of 3 -body H 2 formation heating 3 body H 2 formation heating Dust cooling

Without rotation [M/H] =-4. 5 [M/H] =-5. 5

With rotation [M/H]=-4. 5 [M/H]=-5. 5

Rule of thumb Fragmented Axis Ratio-1 Not fragmented For filament fragmentation, elongation > 30 is required.

Summary 1: (1) Filament fragmentation is one mode of fragmentatation which can generate small mass objects (2) Starting from a finite-size-cloud core with moderate initial elongation, elongation is supressed in the case with gamma>1. 1 (3) Dust cooling in metal deficient clouds as low as 10^-5~10^-6 Zsun provides the possible thermal evolution in which filament fragmentation works, provided that moderate elongation ~1: 2 exists at the onset of dust cooling. (4) If the cloud is suffered from sudden heating process before dust cooling, axis ratio becomes close to unity and filament fragmentation can not be expected even with dust cooling. (5) With the rotation, elongation become larger but the effect is limited.

Effect of isothermal temperature floor by CMB (Preliminary results)

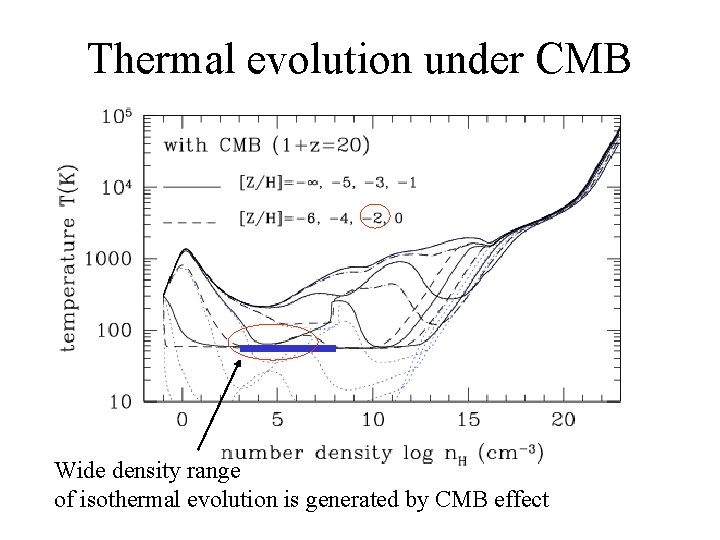
Thermal evolution under CMB Wide density range of isothermal evolution is generated by CMB effect

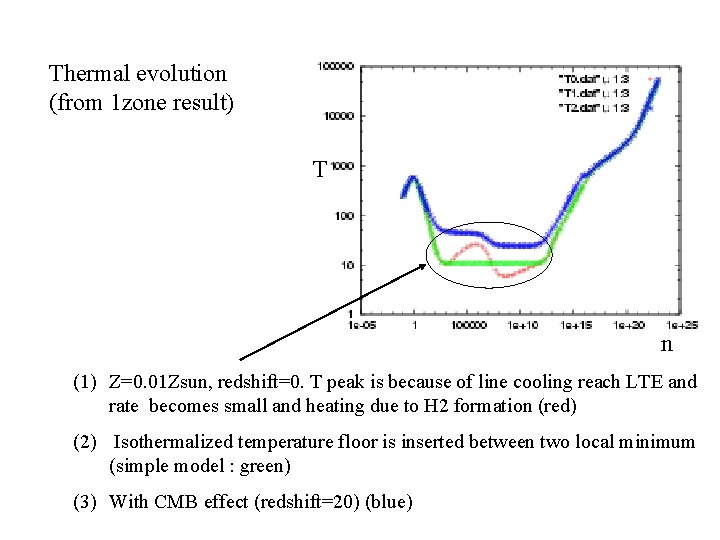
Thermal evolution (from 1 zone result) T n (1) Z=0. 01 Zsun, redshift=0. T peak is because of line cooling reach LTE and rate becomes small and heating due to H 2 formation (red) (2) Isothermalized temperature floor is inserted between two local minimum (simple model : green) (3) With CMB effect (redshift=20) (blue)

Model: (1) Prepare uniform sphere with |Eg|=|Eth| (2) Elongate it to with keeping mass and density to Axis ratio = 1: 2 pi, 1: 5, 1: 4, 1: 3, 1: 2 (3) Follow the gravitational collapse Initial density n=10 Nsph=10^6 Result : final density so far (n=4 e 6) (1) Bounce -> No collapse 1: 2 pi, 1: 5 (2) Collapse -> filament formation -> fragmentation 1: 4, 1: 3 (3) Collapse -> filament formation -> Jeans Condition 1: 2 (4) Collapse -> almost spherical (not calculated) 1: 1. 01 etc.

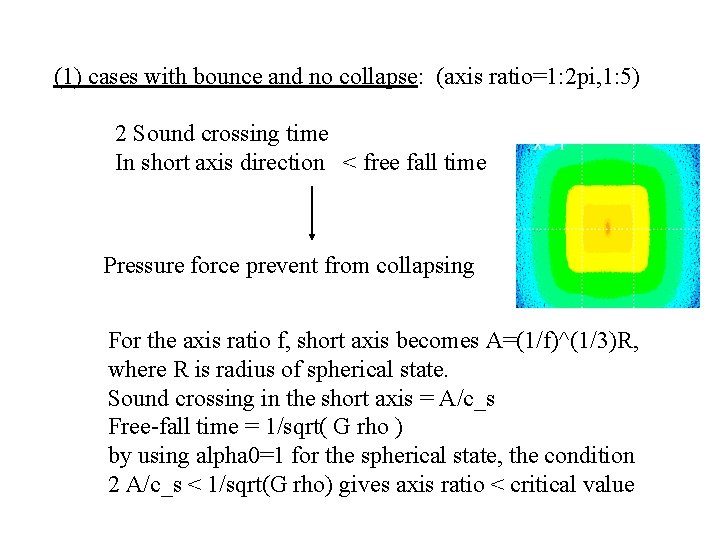
(1) cases with bounce and no collapse: (axis ratio=1: 2 pi, 1: 5) 2 Sound crossing time In short axis direction < free fall time Pressure force prevent from collapsing For the axis ratio f, short axis becomes A=(1/f)^(1/3)R, where R is radius of spherical state. Sound crossing in the short axis = A/c_s Free-fall time = 1/sqrt( G rho ) by using alpha 0=1 for the spherical state, the condition 2 A/c_s < 1/sqrt(G rho) gives axis ratio < critical value

(4) Cases with Non-filamentary collapse Axis Ratio Growth Rate rho^0. 354 for quasi-spherical rho^0. 5 for cylindrical shape Condition for filament formation before the first minimum temperature … at n=1 e 3 Since n 0=10, n/n 0=1 e 2, therefore even initial cylindrical Shape is assumed, we need at least Initial axis ratio > 2 pi/sqrt(1 e 2) = 2 pi/10 = 0. 628 … 1: 1. 628 For smaller than this value, cloud is expected to not to be Filamentally shape enough to fragment.

(2), (3) Collapse & Filament Formation Initial Axis ratio = 1: 4, 1: 3, and 1: 2 In these cases, growth rate of axis ratio is rho^0. 5. 2 Sound crossing time is larger than free-fall time. Therefore, axis ratio becomes larger than 2 pi before n=10^3 and collapse does not halted in the early state. There is another condition, Sound crossing time in short axis < free-fall time Rarefaction wave reach the center of axis Central region of the filament becomes equilibrium Central bounce This condition seems to be between the cases with 1: 3 and 1: 2

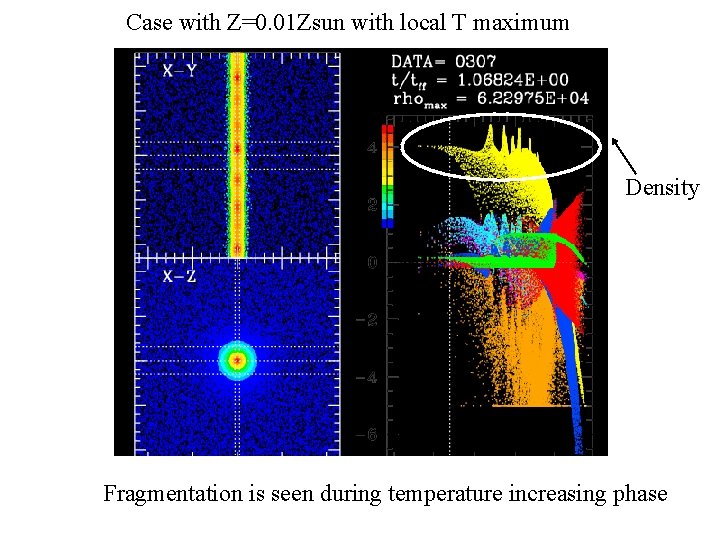
Case with Z=0. 01 Zsun with local T maximum Density Fragmentation is seen during temperature increasing phase

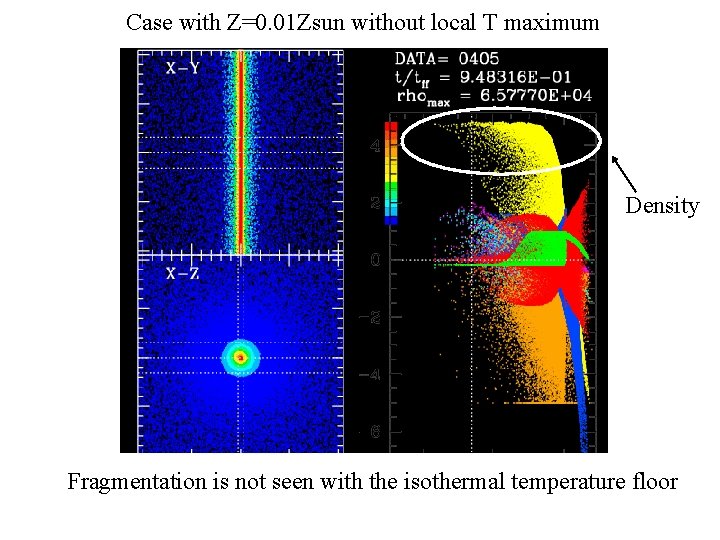
Case with Z=0. 01 Zsun without local T maximum Density Fragmentation is not seen with the isothermal temperature floor

1: 2 … no central bounce further filament collapse no fragmentation, spindle formation fragmentation later 1: 3, 1: 4 … central bounce and equilibrium filamentary core dynamical time become larger than free-fall time fragmentation can be expected here. Numerical Result: 1: 2 … no fragmentation before T local maximum 1: 3 … fragmented 1: 4 … fragmented (just after local T minimum)

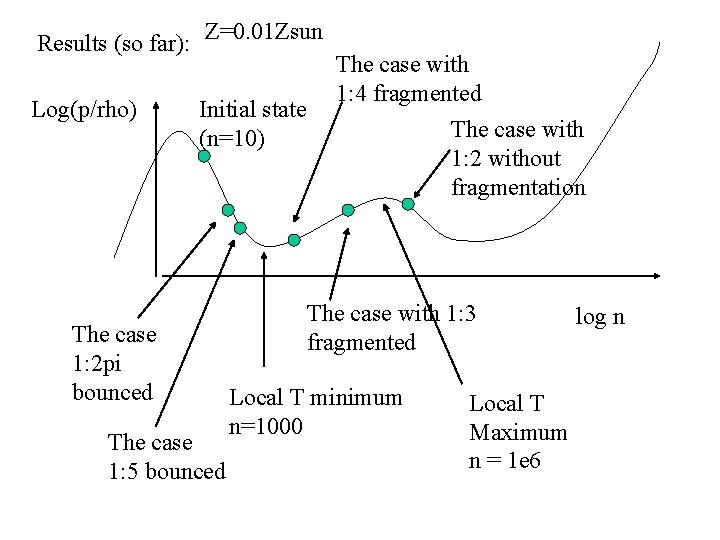
Results (so far): Z=0. 01 Zsun Log(p/rho) Initial state (n=10) The case 1: 2 pi bounced The case 1: 5 bounced The case with 1: 4 fragmented The case with 1: 2 without fragmentation The case with 1: 3 fragmented Local T minimum n=1000 Local T Maximum n = 1 e 6 log n

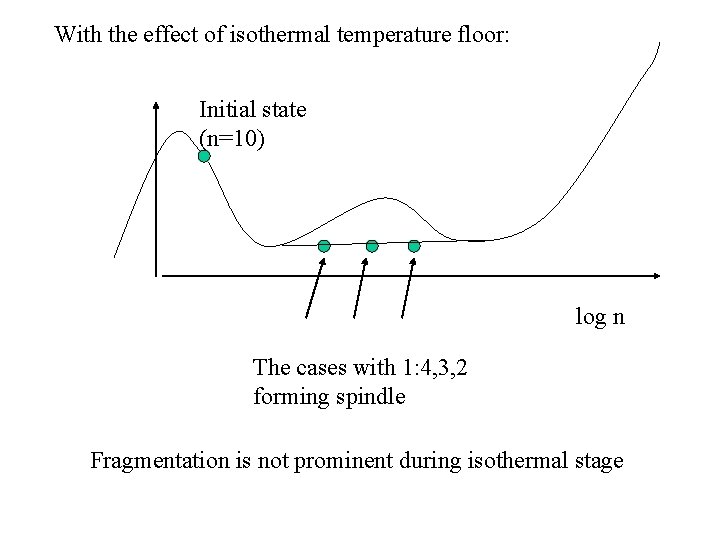
With the effect of isothermal temperature floor: Initial state (n=10) log n The cases with 1: 4, 3, 2 forming spindle Fragmentation is not prominent during isothermal stage

Discussion (preliminary) • For a cloud with dust, filament fragmentation may be effective for clouds with moderate initial elongation • Once filament is formed, fragmentation can be possible at the continuous density range where T is weakly increasing (not only just after the temperature minimum). • Fragmentation density (i. e. mass) of above mode depends on the degree of initial elongation. • Once filament fragmentation takes place, in temperature increasing phase, each fragment tend to have highly spherical shape. Further subfragmentation via filament fragmentation may be rare event (still under investigation) but disk fragmentation is not excluded. • In the density range with the isothermalized EOS, perturnation growth is not prominent within the time scale of filament collapse of the whole system indicating smaller mass fragmentation in later stage.