Closures of relations A closure extends a relation

Closures of relations A closure “extends” a relation to satisfy some property. But extends it as little as possible. Definition. The closure of relation R with respect to property P is the relation S that i) contains R ii) satisfies property P iii) is contained in any relation satisfying i) and ii). That is S is the “smallest” relation satisfying i) and ii). 1

Lemma 1. The reflexive closure of R is S = R {(a, a) | a A } =r(R). Proof. In accordance to the definition of a closure, we need to prove three things to show that S is reflexive closure: i) S contains R ii) S is reflexive iii) S is the smallest relation satisfying i) and ii). S contains R and is reflexive by design. Furthermore, any relation satisfying i) must contain R, any satisfying ii) must contain the pairs (a, a), so any relation satisfying both i) and ii) must contain S 2

Lemma 2. The symmetric closure of R is S = R R-1 =s(R) Proof. S is symmetric and contains R. It is also the smallest such. For suppose we have some symmetric relation T with R T. To show that T contains S we need to show that R-1 T. Take any (a, b) R-1 , it implies (b, a) R , and (b, a) T, since R T. But then (a, b) T as well, because T is symmetric by assumption. So, S = R R-1 T. 3

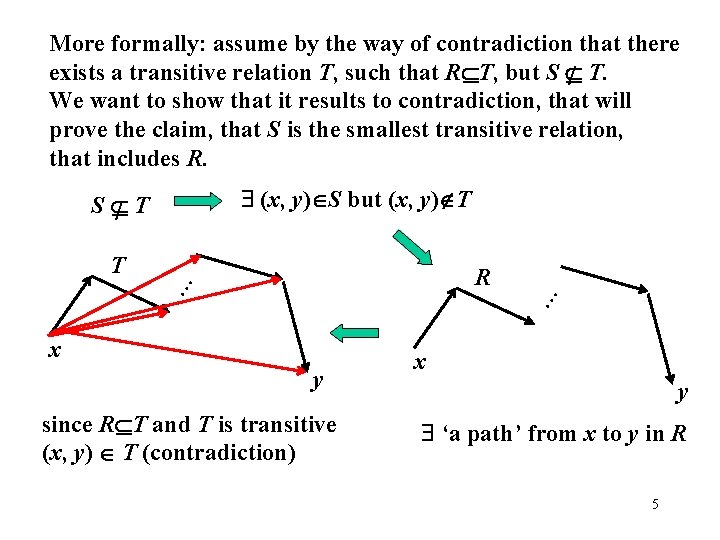
Theorem. The transitive closure of a relation R is the set S = {(a, b) | there is a path from a to b in R}= t (R) Proof. Let’s show that S is transitive. Suppose (a, b) S and (b, c) S. This means there is a path from a to b and a path from b to c in R. If we “concatenate” them (attach the end of the (a, b)-path to the start of the (b, c)-path) we get a path from a to c. Thus, (a, c) S and S is transitive. We need to show, that any transitive relation T containing R contains S. Let’s prove by contradiction. Assume that there exists a transitive relation T containing R, that is smaller then S. 4

More formally: assume by the way of contradiction that there exists a transitive relation T, such that R T, but S / T. We want to show that it results to contradiction, that will prove the claim, that S is the smallest transitive relation, that includes R. (x, y) S but (x, y) T S /T T … … R x y since R T and T is transitive (x, y) T (contradiction) x y ‘a path’ from x to y in R 5

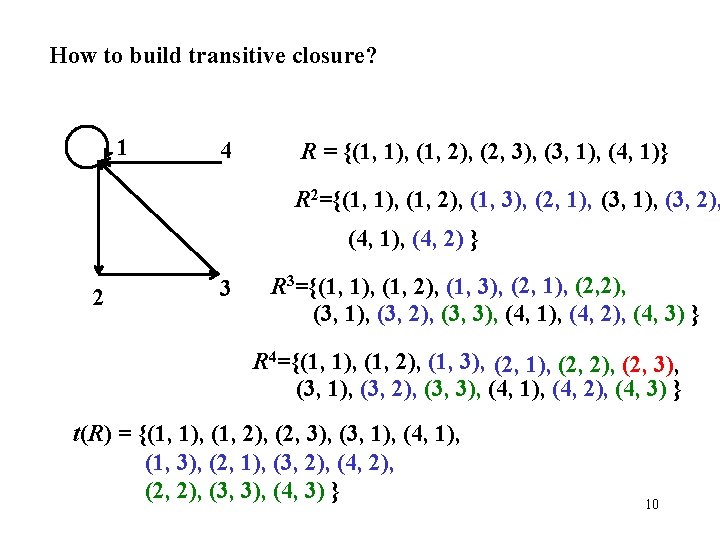
An alternative way to represent transitive closure is as the union of paths with different length t (R) = S 1 S 2 S 3 … where Sn = {(a, b) | there is a path of length n from a to b in R } Theorem. (a, b) Rn iff there is a path of length n in R. (will be proved later by induction) Thus, we can prove the following equivalent definition of transitive closure Lemma 3. The transitive closure of the relation R is t(R) = R R 2 R 3… (left for you to prove) 6

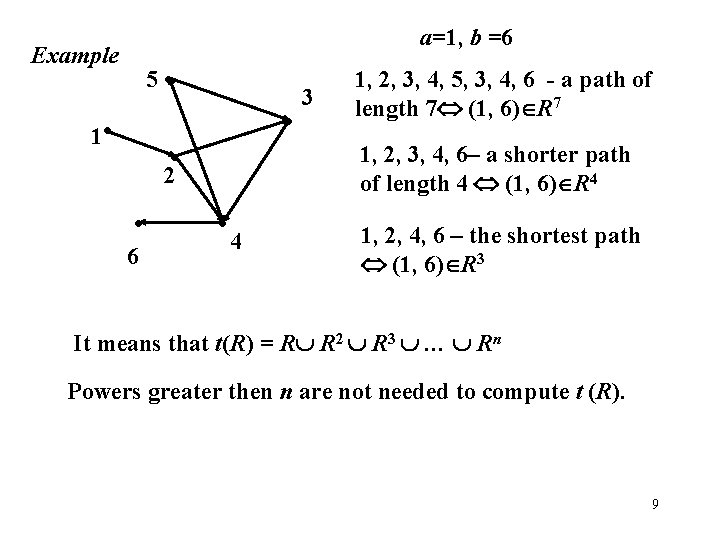
How many powers of R we need to find t (R)? It turns out that if |A|=n, we don’t need powers greater then n. Theorem. Suppose R is a relation on a set A, R A A, |A|=n, and there is a path of length m > n from a to b in R. Then there is a path from a to b of length less or equal n. Example: n =4 a • b • c There is a path of length 5 from a to a there is a shorter path. 7

Proof. Assume that there exists a path x 0, x 1, …, xm , a = x 0 and b = xm, of length m, m>n. Then you have m “pigeons” and n “holes”, m >n. By Pigeonhole principle, at least two of vertices should coincide: xi=xj for some i < j (some vertex visited twice on the path). It means that we can cut off a loop and make a shorter path from a to b. The length of a path from a to b, is at most n (n 1, if a b). 8

a=1, b =6 Example 5 • • 1, 2, 3, 4, 6– a shorter path of length 4 (1, 6) R 4 • 2 • 6 3 1, 2, 3, 4, 5, 3, 4, 6 - a path of length 7 (1, 6) R 7 • 4 1, 2, 4, 6 – the shortest path (1, 6) R 3 It means that t(R) = R R 2 R 3 … Rn Powers greater then n are not needed to compute t (R). 9

We can also define a composition of closures, e. g. tr(R) = t(r(R)), rs(R)=r(s(R)), etc. It turns out, that the order of composition does matter. Theorem. For any binary relation R A A st(R) ts(R). By theorem about symmetric and transitive closures st(R) = s(t(R)) = t(R) (t(R))-1 = (R R 2 R 3 …)-1 ts(R) = t(s(R)) = t(R R-1) = (R R-1)2 (R R-1)3… By the distributive property of composition over union (R R-1)2= (R R-1) = R (R R-1) R-1 (R R-1) = R R-1 R R-1 = R 2 R R-1 R R-2, where R-1= R-2 11

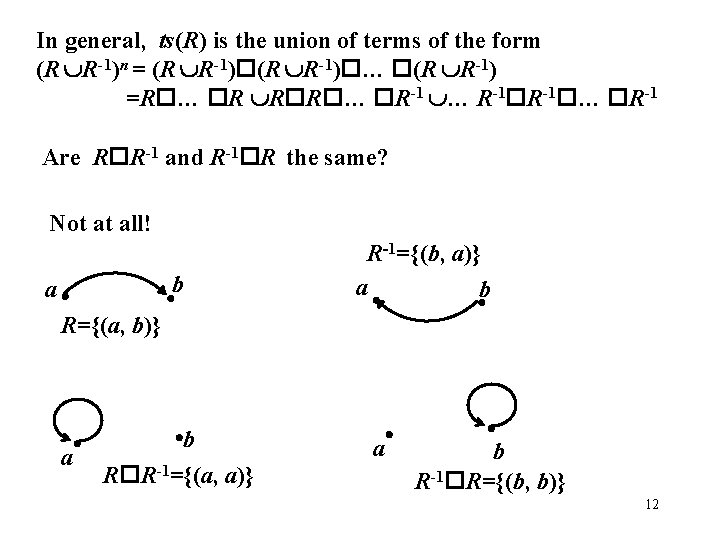
In general, ts(R) is the union of terms of the form (R R-1)n = (R R-1) … (R R-1) =R … R R R … R-1 R-1 … R-1 Are R R-1 and R-1 R the same? Not at all! b a R-1={(b, a)} a b R={(a, b)} a b R R-1={(a, a)} a b R-1 R={(b, b)} 12

We can observe, that ts(R) includes compositions of all possible sequences of R and R-1, while st(R) is a union of positive and negative powers of R (but not mixtures). So, it can be proved that st(R) ts(R), but ts(R) st(R). Proof. Take arbitrary (x, y) st(R) to show that (x, y) ts(R). By the Lemma 2 (x, y) st(R) implies that (x, y) t(R) (t(R))-1. We have two cases. Case 1: (x, y) t(R), i. e. there exists a path from x to y in R. It implies that there exist a path from x to y in s(R), since R s(R) = R R-1. By the definition of transitive closure it means that (x, y) t(s(R)). Case 2: (x, y) (t(R))-1 , i. e. (y, x) t(R), and similar to the case 1, there exists a path from y to x in R, that implies the path in s (R). It implies there exists a path from x to y, or (x, y) ts(R). Try to find a counterexample to disproves that ts(R) st(R). 13

Equivalence relations and partitions. Consider the following relation on a set of all people: B = {(x, y)| x has the same birthday as y } B is reflexive, symmetric and transitive. We can think about this relation as splitting all people into 366 categories, one for each possible day. Definition. A relation R A A is called an equivalence relation on A if it is symmetric, reflexive and transitive. An equivalence relation on a set A represents some partition of this set. 14

Definition. For any set A subsets Ai A partition set A if • A = A 1 A 2 … An • Ai Aj= , for any i j. • Ai for any i A A 2 A 1 A 4 A 3 Example. A={1, 2, 3, 4}, ={{2}, {1, 3}, {4}} is a partition of A. 15

Definition. Suppose R is equivalence relation on a set A, and x A. Then the equivalence class of x with respect to R is the set [x]R={y A| y. Rx} In the case of the same birthday relation B, if p is any person, then the equivalence class of p [p]B={q P | p. Bq} ={q P | q has the same birthday as p} For example, if John was born on Aug. 10, [John]B= {q P | q was born on Aug. 10} The set of all equivalence classes of elements of A is called A modulo R and is denoted A/R: A/R={[x]R | x A} 16

We are going to prove that any equivalence relation R on A induces a partition of A and any partition of A gives rise to an equivalence relation. Theorem 1. Suppose R is an equivalence relation on a set A. Then A/R ={[x]R | x A} is a partition of A. Proof. To prove that A/R defines a partition, we must prove three properties of a partition. 1) The union of all equivalence classes [x]R equals A, i. e. Since any equivalence class is a subset of A, their union is also a subset of A. So, all we need to show is To prove this, suppose x A. Then x [x]R because [x]R ={y A | y. Rx }and x. Rx due to reflexive property of R. 17

x [x]R implies 2) To prove that A/R is pairwise disjoint we need to show, that for any x, y A if [x] [y] then [x] [y]=. It is easier to prove the contrapositive: if [x] [y] , then [x]=[y]. So, assume [x] [y] , then we can find an element z [x] [y]. It implies that x. Rz and z. Ry by definition of equivalence classes. Then x. Rz and z. Ry implies x. Ry due to transitive property of R. We now claim that [x] [y]. Take any a [x], it implies a. Rx, which implies a. Ry because of x. Ry and transitive property of R. a. Ry implies a [y], i. e. [x] [y]. Similarly [y] [x], or [x]=[y]. 3) None of equivalence classes is empty, because for any x A, x [x]. 18

Theorem 2. Suppose A is a set and is a partition of A, i. e. is a set of disjoint nonempty subsets, such that any element of A belongs to exactly one subset. Then the relation R on A defined as R = {(x, y) | x, y A and x and y belong to the same subset in } is an equivalence relation on A. Proof. We need to prove that R is reflexive, symmetric and transitive. • R is reflexive because for any x A, x and itself belong to the same subset in . • R is obviously symmetric • Suppose x. Ry and y. Rz, that is x and y belong to the same subset and y and z belong to the same subset. This implies that x and z belong to the same subset in , thus x. Rz. 19

Definition. A partition P 2 is called a refinement of P 1 if every set in P 2 is a subset of one of sets in P 1. Example. Consider the partition P 1. ={{1, 3, 5, 7, 9}, {2, 4, 6, 8, 10}}, induced by the relation R 1 = {(x, y) | x = y mod(2)} on a set A = {1, 2, … 10}. Then the relation R 2 = {(x, y) | x = y mod(4)} induces a partition P 2. ={{1, 5, 9}, {3, 7}, {2, 6, 10}, {4, 8}}, which is a refinement of P 1. Theorem. Suppose R 1 and R 2 are equivalence relations on a set A. Let P 1 and P 2 are partitions that correspond to R 1 and R 2 respectively Then R 1 R 2 iff P 1 is a refinement of P 2 20

Partial Orders. A particular type of binary relation on a set. Definition. A binary relation R A A is a partial order, if it is reflexive, transitive and anti-symmetric. The set A together with the partial order relation is called a poset. Examples: ‘less or equal’ ‘greater or equal’ ‘subset’ relation ‘divides’ 21

Functions. Function is a special type of relation. Recall that in a relation R A B an element a A may be related to more then one element of B, or it may be not related to any. Definition. A function f : A B is a binary relation from A to B such that, for every a A there exists a unique (i. e. exactly one) element b B such that (a, b) f. If a A, write f(a) for corresponding element of B, b= f(a) A = domain f a a is the pre-image of b b= f(a) B = co-domain. b is the image of a; 22

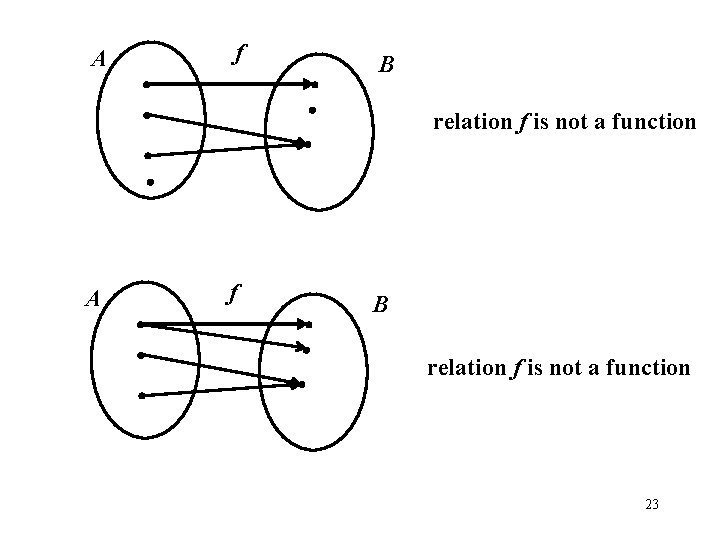
f A B relation f is not a function f A B relation f is not a function 23

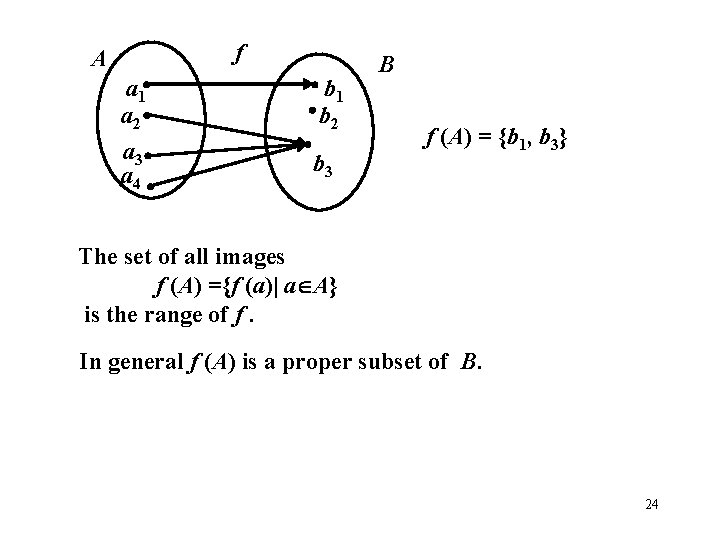
f A a 1 a 2 b 1 b 2 a 3 a 4 b 3 B f (A) = {b 1, b 3} The set of all images f (A) ={f (a)| a A} is the range of f. In general f (A) is a proper subset of B. 24

Assume |A|=n, |B|=m. How many different functions f : A B exist? Recall that there are 2 n m different relations R A B, but not all of them are functions. For relations we counted all subsets of A B. A function must include exactly n pairs, one for each element in A. Each of elements from the domain can be related to any element from co-domain. So, we have m choices for each pair, the total number of functions is mn. where 25

Properties of functions (surjective, injective, bijective ) Definition. Surjective (“onto”): range = co-domain. A function f : A B is called surjective, if for any b B there exists a A, such that f (a) = b. b B, a A (f (a)=b) f A a 1 a 2 b 1 b 2 a 3 a 4 B b 3 This function is not surjective because b 2 does not have any pre-image. 26

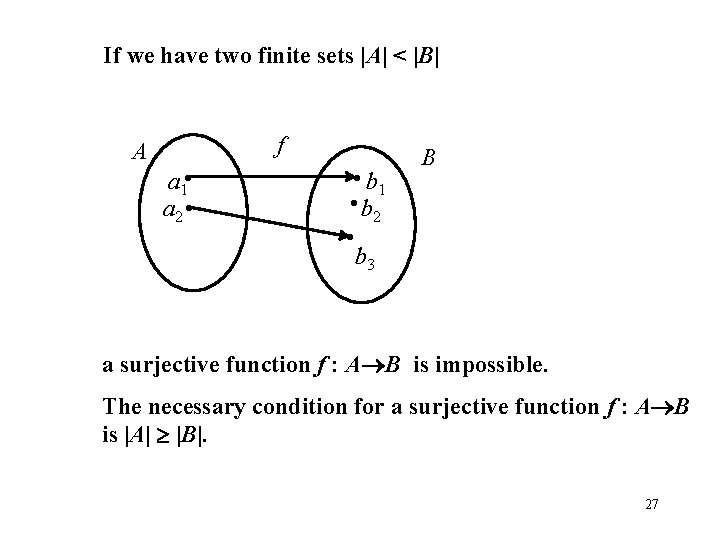
If we have two finite sets |A| < |B| f A a 1 a 2 b 1 b 2 B b 3 a surjective function f : A B is impossible. The necessary condition for a surjective function f : A B is |A| |B|. 27

Definition. Injective (“one-to-one”): a 1, a 2 A, a 1 a 2 f (a 1) f (a 2) A function f : A B is called injective, if for all a 1, a 2 A, a 1 a 2 f (a 1) f (a 2). Equivalently, it means f (a 1) = f (a 2) a 1 = a 2 f A a 1 a 2 a 3 b 1 B b 2 This function is not injective. 28

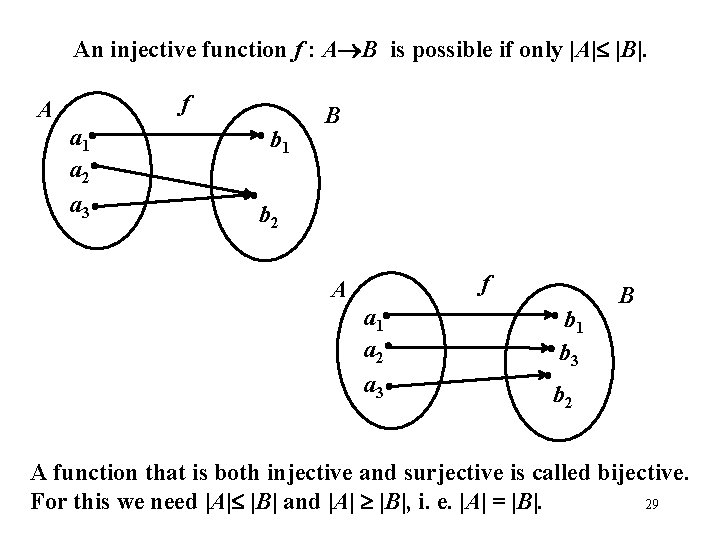
An injective function f : A B is possible if only |A| |B|. f A a 1 a 2 a 3 b 1 B b 2 f A a 1 a 2 a 3 b 1 b 3 B b 2 A function that is both injective and surjective is called bijective. For this we need |A| |B| and |A| |B|, i. e. |A| = |B|. 29

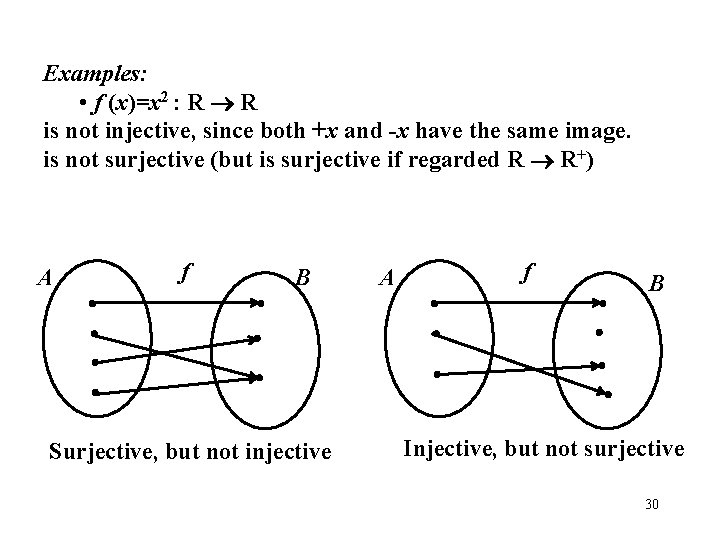
Examples: • f (x)=x 2 : R R is not injective, since both +x and -x have the same image. is not surjective (but is surjective if regarded R R+) f A B f A Surjective, but not injective B Injective, but not surjective 30

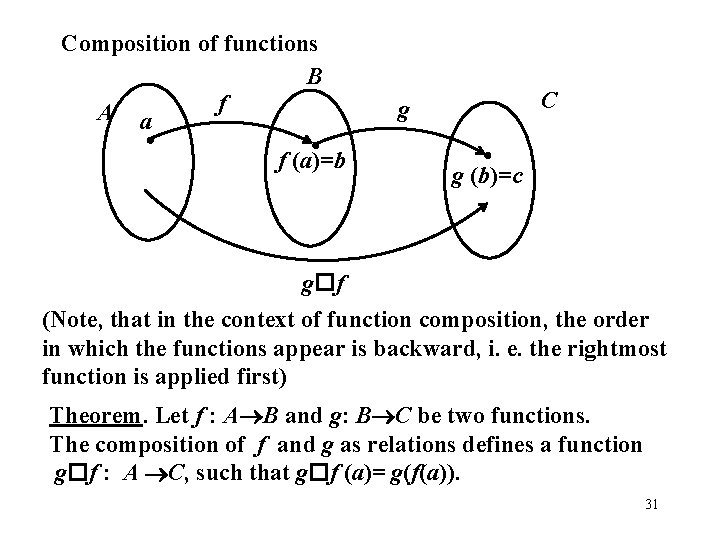
Composition of functions B f A a f (a)=b C g g (b)=c g f (Note, that in the context of function composition, the order in which the functions appear is backward, i. e. the rightmost function is applied first) Theorem. Let f : A B and g: B C be two functions. The composition of f and g as relations defines a function g f : A C, such that g f (a)= g(f(a)). 31

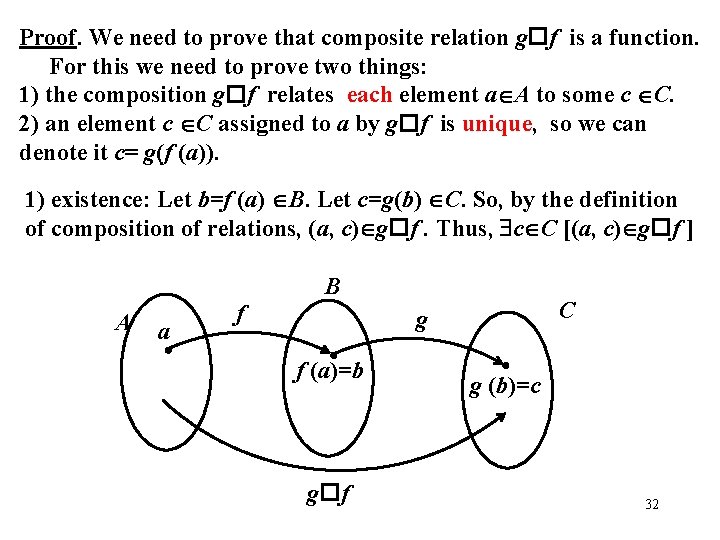
Proof. We need to prove that composite relation g f is a function. For this we need to prove two things: 1) the composition g f relates each element a A to some c C. 2) an element c C assigned to a by g f is unique, so we can denote it c= g(f (a)). 1) existence: Let b=f (a) B. Let c=g(b) C. So, by the definition of composition of relations, (a, c) g f. Thus, c C [(a, c) g f ] B A a f C g f (a)=b g f g (b)=c 32

2) uniqueness: Suppose (a, c 1) g f and (a, c 2) g f. Then by the definition of composition, b 1 B, such that (a, b 1) f and (b 1, c 1) g, and b 2 B, such that (a, b 2) f and (b 2, c 2) g. Since f is a function, there may be only one b B, such that (a, b) f, so b 1= b 2. Since g is a function, (b, c 1) g and (b, c 2) g imply that c 1= c 2. b 1 g f a c 1 b 2 c 2 Thus, (g f )(a)= c= g (b) = g (f (a)). 33