Closest Pair Given a set S p 1

Closest Pair Given a set S = {p 1, p 2, . . . , pn} of n points in the plane find the two points of S whose distance is the smallest.

Closest Pair – Naïve Algorithm Pseudo code for each pt i S for each pt j S and i<>j { compute distance of i, j if distance of i, j < min_dist = distance i, j } return min_dist n n Time Complexity– O(n 2) Can we do better?

Closest Pair – Divide & Conquer n Divide the problem into two equal-sized sub problems n Solve those sub problems recursively n Merge the sub problem solutions into an overall solution

Closest Pair – Divide & Conquer n Assume that we have solutions for sub problems S 1, S 2. n How can we merge in a time-efficient way? n n n The closest pair can consist of one point from S 1 and another from S 2 Testing all posibilities requires: O(n/2) · O(n/2) O(n 2) Not good enough

Closest Pair – Divide & Conquer dimension d = 1 n n n Partition S, a set of points on a line, into two sets S 1 and S 2 at some point m such that for every point p S 1 and q S 2 , p < q. Solve Closest Pair recursively on S 1 and S 2 Let 1 be the smallest distance in S 1 and 2 in S 2 Let be the smallest distance found so far: = min ( 1, 2) What is the closest pair in S? n Either {p 1, p 2} or {q 1, q 2} or some {p 3, q 3} with p 3 S 1 and q 3 S 2. S 1 p 2 S 2 p 3 q 3 m q 1 q 2

Closest Pair – Divide & Conquer dimension d = 1 n To find a pair {p 3, q 3}, Is it necessary to check all possible pairs? n n How many points of S 1 or S 2 can lie within of m? n n n No Since is the distance between the closest pair in either S 1 or S 2, there can only be at most 1 point in each side. Therefore, the number of distance computations required to check for a closest pair {p 3, q 3} with p 3 S 1 and q 3 S 2 is O(1). Thus, the time complexity is n O(n log n) S 1 p 2 p 3 q 3 m S 2 q 1 q 2

Closest Pair – Divide & Conquer dimension d = 2 n n n Partition two dimensional set S into subsets S 1 and S 2 by a vertical line l at the median x coordinate of S. Solve the problem recursively on S 1 and S 2. Let {p 1, p 2} be the closest pair in S 1 and {q 1, q 2} in S 2. Let 1 = distance(p 1, p 2) and 2 = distance(q 1, q 2) Let = min( 1, 2) S 1 l S 2 p 1 1 p 2 q 1 q 2 2

Closest Pair – Divide & Conquer dimension d = 2 n n n In order to merge we have to determine if exists a pair of points {p, q} where p S 1, q S 2 and distance(p, q) < . If so, p and q must both be within of l. Let P 1 and P 2 be vertical regions of the plane of width on either side of l. If {p, q} exists, p must be within P 1 and q within P 2. For d = 1, there was at most one candidate point for p and one for q. For d = 2, every point in S 1 and S 2 may be a candidate, as long as each is within of l, which implies: O(n/2) = O(n 2) Can we do better ? P 1 l P 2 p 1 S 1 1 q 1 S 2 p 2 2 q 2

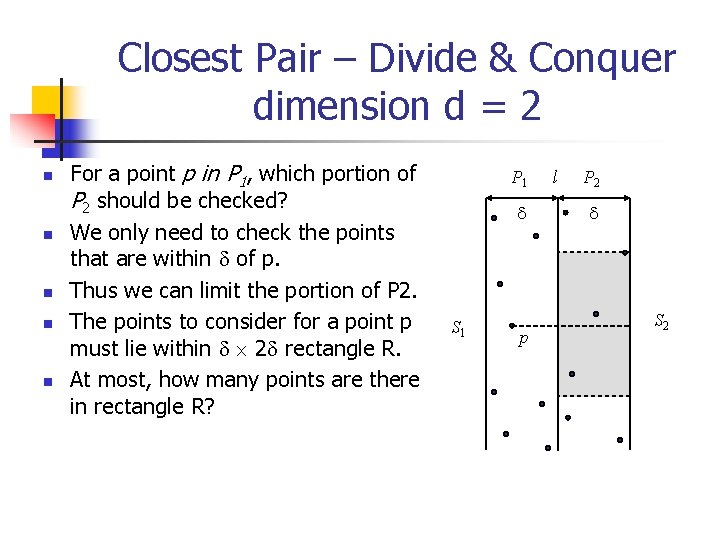
Closest Pair – Divide & Conquer dimension d = 2 n n n For a point p in P 1, which portion of P 2 should be checked? We only need to check the points that are within of p. Thus we can limit the portion of P 2. The points to consider for a point p must lie within 2 rectangle R. At most, how many points are there in rectangle R? P 1 S 1 p l P 2 S 2

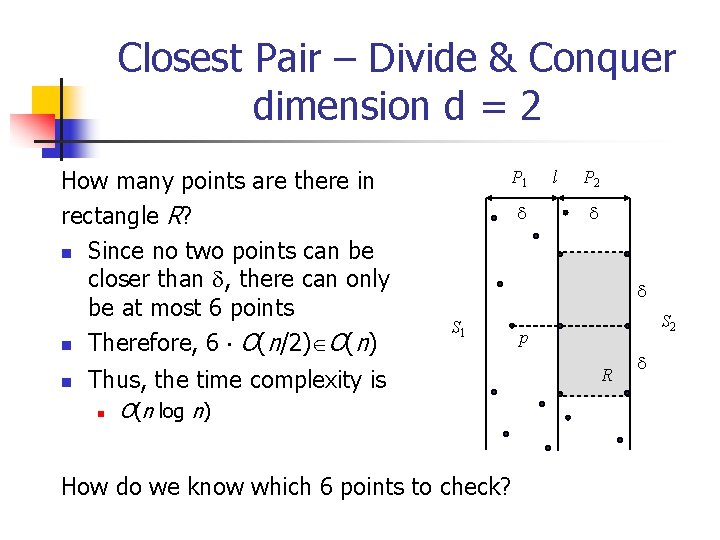
Closest Pair – Divide & Conquer dimension d = 2 How many points are there in rectangle R? n Since no two points can be closer than , there can only be at most 6 points n Therefore, 6 O(n/2) O(n) n P 1 P 2 S 1 Thus, the time complexity is n l O(n log n) How do we know which 6 points to check? S 2 p R

Closest Pair – Divide & Conquer dimension d = 2 How do we know which 6 points to check? n Project p and all the points of S 2 within P 2 onto l. n Only the points within of p in the y projection need to be considered (max of 6 points). n After sorting the points on y coordinate we can find the points by scanning the sorted lists. Points are sorted by y coordinates only once. n To prevent resorting in O(n log n) in each merge, two previously sorted lists are merged in O(n). Time Complexity: O(n log n)