ClosedForm MSE Performance of the Distributed LMS Algorithm

Closed-Form MSE Performance of the Distributed LMS Algorithm Gonzalo Mateos, Ioannis Schizas and Georgios B. Giannakis ECE Department, University of Minnesota Acknowledgment: ARL/CTA grant no. DAAD 19 -01 -2 -0011 USDo. D ARO grant no. W 911 NF-05 -1 -0283 1

Motivation n Estimation using ad hoc WSNs raises exciting challenges q q q n Unique features q q n Communication constraints Single-hop communications Limited power budget Lack of hierarchy / decentralized processing Consensus Environment is constantly changing (e. g. , WSN topology) Lack of statistical information at sensor-level Bottom line: algorithms are required to be q q q Resource efficient Simple and flexible Adaptive and robust to changes 2

Prior Works n Single-shot distributed estimation algorithms q q q n n Consensus averaging [Xiao-Boyd ’ 05, Tsitsiklis-Bertsekas ’ 86, ’ 97] Incremental strategies [Rabbat-Nowak etal ’ 05] Deterministic and random parameter estimation [Schizas etal ’ 06] Consensus-based Kalman tracking using ad hoc WSNs q MSE optimal filtering and smoothing [Schizas etal ’ 07] q Suboptimal approaches [Olfati-Saber ’ 05], [Spanos etal ’ 05] Distributed adaptive estimation and filtering q LMS and RLS learning rules [Lopes-Sayed ’ 06 ’ 07] 3

Problem Statement n Ad hoc WSN with sensors q q q Single-hop communications only. Sensor ‘s neighborhood Connectivity information captured in Zero-mean additive (e. g. , Rx) noise n Goal: estimate a signal vector n Each sensor q q n , at time instant Acquires a regressor and scalar observation Both zero-mean and spatially uncorrelated Least-mean squares (LMS) estimation problem of interest 4

Power Spectrum Estimation n Find spectral peaks of a narrowband (e. g. , seismic) source q q q AR model: Source-sensor multi-path channels modeled as FIR filters Unknown orders and tap coefficients n Observation at sensor is n Define: n Challenges q q Data model not completely known Channel fades at the frequencies occupied by 5

A Useful Reformulation Introduce the bridge sensor subset n 1) 2) n For all sensors , such that For , a path connecting them devoid of edges linking two sensors Consider the convex, constrained optimization Proposition [Schizas etal’ 06]: For WSN is connected, then satisfying 1)-2) and the 6

Algorithm Construction n Associated augmented Lagrangian n Two key steps in deriving D-LMS 1) Resort to the alternating-direction method of multipliers Gain desired degree of parallelization 2) Apply stochastic approximation ideas Cope with unavailability of statistical information 7

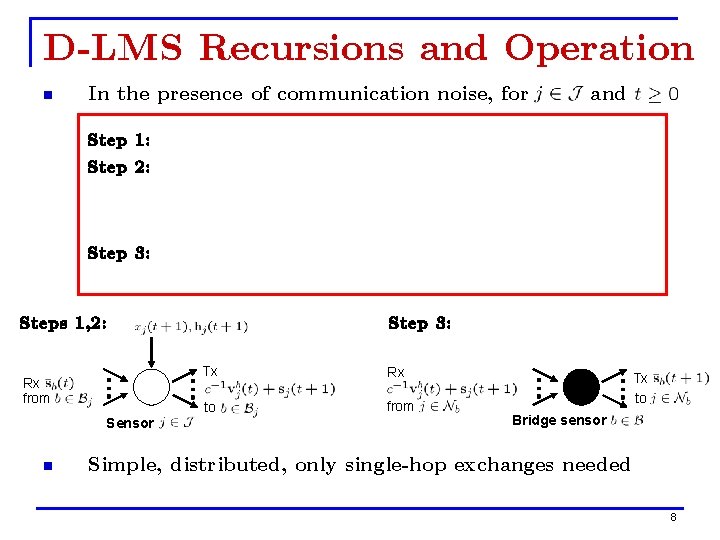
D-LMS Recursions and Operation n In the presence of communication noise, for and Step 1: Step 2: Step 3: Steps 1, 2: Rx from Sensor n Step 3: Tx Rx to from Tx to Bridge sensor Simple, distributed, only single-hop exchanges needed 8

Error-form D-LMS Study the dynamics of n q q Local estimation errors: Local sum of multipliers: (a 1) Sensor observations obey where the zero-mean white noise n Introduce and Lemma: Under (a 1), for and has variance then where consists of the blocks with 9

Performance Metrics n Local (per-sensor) and global (network-wide) metrics of interest (a 2) (a 3) is white Gaussian with covariance matrix and are independent n Define n Customary figures of merit q q q MSD EMSE Local Global 10

Tracking Performance (a 4) Random-walk model: mean white with covariance n n Let Convenient c. v. : where ; independent of where Proposition: Under (a 2)-(a 4), the covariance matrix of with is zeroand obeys . Equivalently, after vectorization where 11

Stability and S. S. Performance Proposition: Under (a 1)-(a 4), the D-LMS algorithm achieves consensus in the mean, i. e. , the step-size is chosen such that q provided with MSE stability follows n Intractable to obtain explicit bounds on Proposition: Under (a 1)-(a 4), the D-LMS algorithm is MSE stable for sufficiently small q From stability, has bounded entries n The fixed point of is n Enables evaluation of all figures of merit in s. s. 12

Step-size Optimization n If n Not surprising q q optimum minimizing EMSE Excessive adaptation MSE inflation Vanishing tracking ability lost n Recall n Hard to obtain closed-form , but easy numerically (1 -D). 13

Simulated Tests node WSN, Rx AWGN w/ Regressors: , w/ ; i. i. d. ; w/ Observations: linear data model, WGN w/ , D-LMS: Time-invariant parameter: Random-walk model: 14

Concluding Summary n Developed a distributed LMS algorithm for general ad hoc WSNs n Detailed MSE performance analysis for D-LMS q q n Analysis under the simplifying white Gaussian setting q q q n Stationary setup, time-invariant parameter Tracking a random-walk Closed-form, exact recursion for the global error covariance matrix Local and network-wide figures of merit for and in s. s. Tracking analysis revealed minimizing the s. s. EMSE Simulations validate theoretical findings q Results extend to temporally-correlated (non-) Gaussian sensor data 15