Close Packed Crystals Part of MATERIALS SCIENCE A

Close Packed Crystals Part of MATERIALS SCIENCE & A Learner’s Guide ENGINEERING AN INTRODUCTORY E-BOOK Anandh Subramaniam & Kantesh Balani Materials Science and Engineering (MSE) Indian Institute of Technology, Kanpur- 208016 Email: anandh@iitk. ac. in, URL: home. iitk. ac. in/~anandh http: //home. iitk. ac. in/~anandh/E-book. htm

Close Packed Crystals q Initially we consider ‘usual’ type of close packed crystals, which are made of single kind of sphere. q In other types of close packed crystals (e. g. tetrahedrally close packed crystals, also called topologically close packed crystals), more than one size of sphere may be involved. q One may even conceive of close packing of ellipsoids and other non-spherical objects. q Cubic Close Packed (CCP- commonly called FCC crystal also) and Hexagonal Close Packed (HCP) are two common examples of close packed crystals. q The term close packed crystal implies closest packed crystal (having a packing fraction of 0. 74). q The proof that this is the densest crystallographic packing of spheres possible is a difficult one (and will not be considered here). q CCP and HCP are just two examples among a series of close packed structures which can be envisaged (shown in coming slides). q Every atom in these structures has a coordination number of 12 forming a Cubeoctahedron or a Twinned Cubeoctahedron (around the central atom).

q The common starting point is a close packed layer of atoms with 6 -fold symmetry. q Identical layers are stacked one on another with a shift. q The shift is such that the atoms in the above (and below) layers sit in the ‘valleys’ formed by a layer. q All such possibilities (see coming slides) lead to Close Packed Crystals. q The original 6 -fold symmetry present in a single layer is lost on this kind of packing (you must be aware of the 3 -fold present in CCP and HCP crystals!). Yes! HCP crystal has NO true 6 -fold axis!

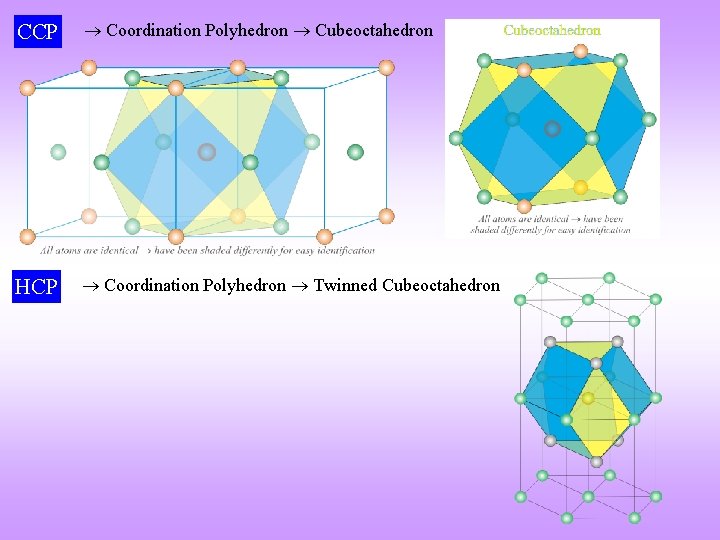
CCP Coordination Polyhedron Cubeoctahedron HCP Coordination Polyhedron Twinned Cubeoctahedron

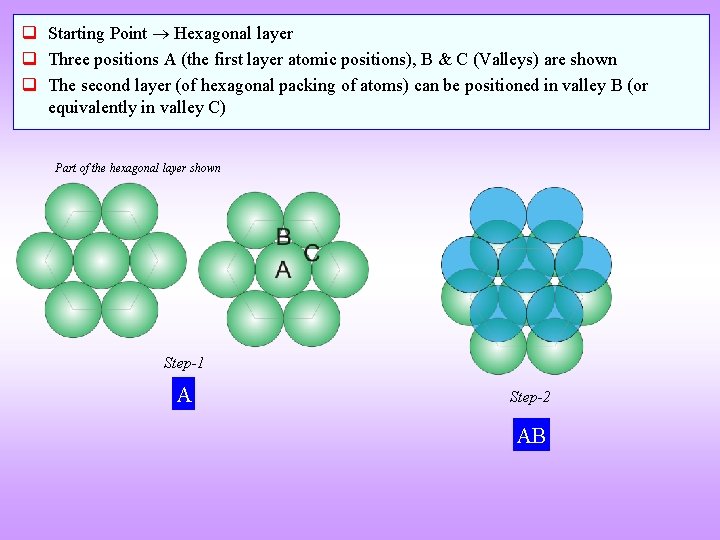
q Starting Point Hexagonal layer q Three positions A (the first layer atomic positions), B & C (Valleys) are shown q The second layer (of hexagonal packing of atoms) can be positioned in valley B (or equivalently in valley C) Part of the hexagonal layer shown Step-1 A Step-2 AB

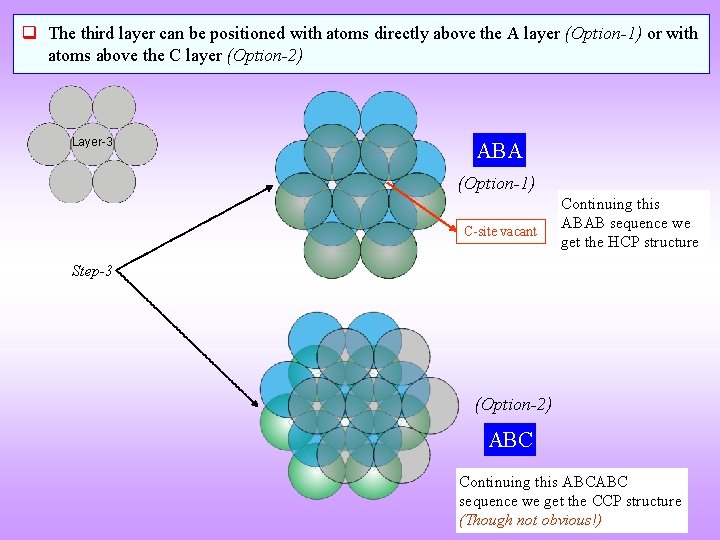
q The third layer can be positioned with atoms directly above the A layer (Option-1) or with atoms above the C layer (Option-2) Layer-3 ABA (Option-1) C-site vacant Continuing this ABAB sequence we get the HCP structure Step-3 (Option-2) ABC Continuing this ABCABC sequence we get the CCP structure (Though not obvious!)

q ABCABC… & ABAB… are just but two amongst the infinite possibilities q At each stage of construction we have a choice of putting an atomic layer at A, B or C position q Possibilites include: ABCAB… ABCABCAB… q Hence we can construct crystals with larger and larger unit cells. q If we randomly put the layers we will not get a crystal in the ‘true sense’. (We can think of these as 2 D crystals, which are not periodic in 3 rd dimension). q Few stages in the infinite choice tree is shown below. B A C B A A B C C B B C Track a branch to infinity or truncate at some stage and repeat to get a structure

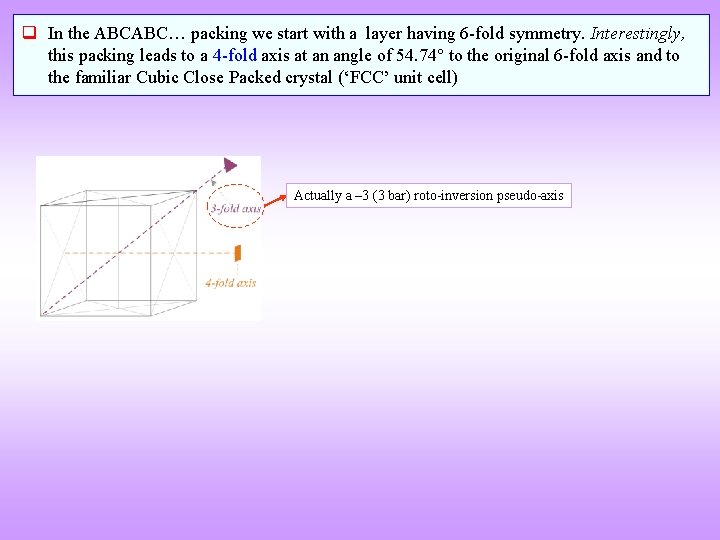
q In the ABCABC… packing we start with a layer having 6 -fold symmetry. Interestingly, this packing leads to a 4 -fold axis at an angle of 54. 74 to the original 6 -fold axis and to the familiar Cubic Close Packed crystal (‘FCC’ unit cell) Actually a – 3 (3 bar) roto-inversion pseudo-axis

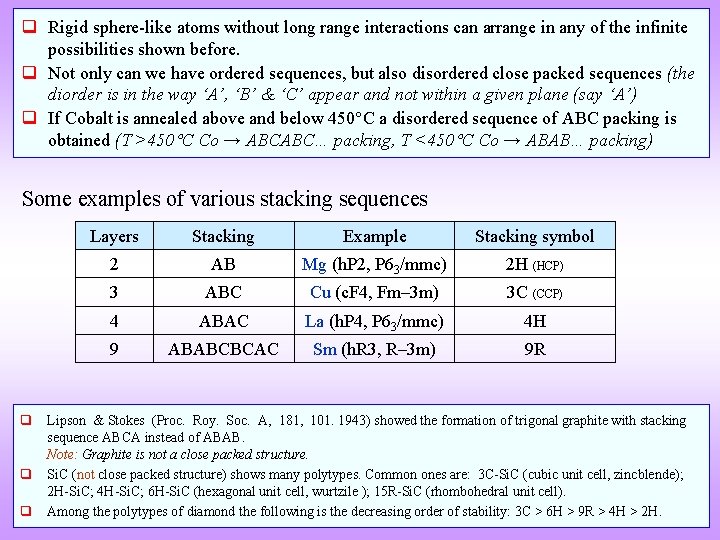
q Rigid sphere-like atoms without long range interactions can arrange in any of the infinite possibilities shown before. q Not only can we have ordered sequences, but also disordered close packed sequences (the diorder is in the way ‘A’, ‘B’ & ‘C’ appear and not within a given plane (say ‘A’) q If Cobalt is annealed above and below 450 C a disordered sequence of ABC packing is obtained (T >450 C Co → ABCABC… packing, T <450 C Co → ABAB… packing) Some examples of various stacking sequences Layers Stacking Example Stacking symbol 2 AB Mg (h. P 2, P 63/mmc) 2 H (HCP) 3 ABC Cu (c. F 4, Fm– 3 m) 3 C (CCP) 4 ABAC La (h. P 4, P 63/mmc) 4 H 9 ABABCBCAC Sm (h. R 3, R– 3 m) 9 R q Lipson & Stokes (Proc. Roy. Soc. A, 181, 101. 1943) showed the formation of trigonal graphite with stacking sequence ABCA instead of ABAB. Note: Graphite is not a close packed structure. q Si. C (not close packed structure) shows many polytypes. Common ones are: 3 C-Si. C (cubic unit cell, zincblende); 2 H-Si. C; 4 H-Si. C; 6 H-Si. C (hexagonal unit cell, wurtzile ); 15 R-Si. C (rhombohedral unit cell). q Among the polytypes of diamond the following is the decreasing order of stability: 3 C > 6 H > 9 R > 4 H > 2 H.

La Closed packed crystal [0001] C layer A layer B layer A layer Lattice parameter(s) a = 3. 77Å, c = 12. 159Å Space Group P 63/mmc (194) Strukturbericht notation Pearson symbol Other examples with this structure hp 4 Wyckoff Site position Symmetry x y z Occupancy La 1 2 a -3 m 0 0 0 1 La 2 2 c -6 m 2 0. 33 0. 67 0. 25 1 Note: All atoms are La

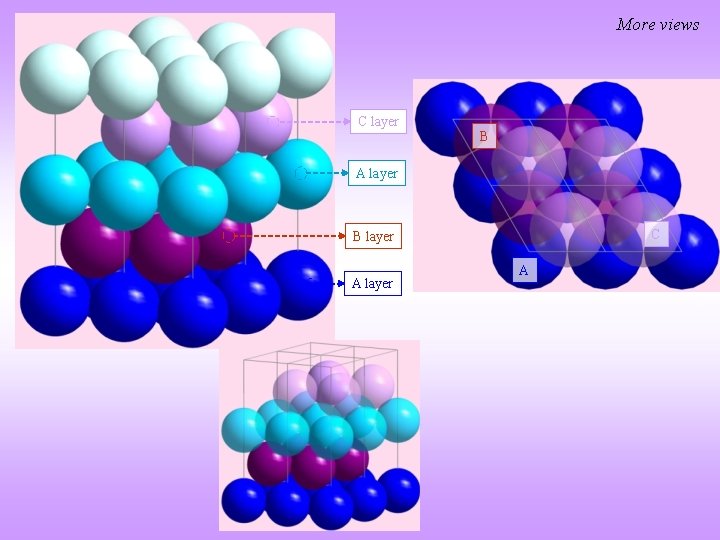
More views C layer B A layer C B layer A