Clip Art courtesy of MS Office 2000 Refrigeration

Clip Art courtesy of MS Office 2000. Refrigeration and Heat Pump Systems

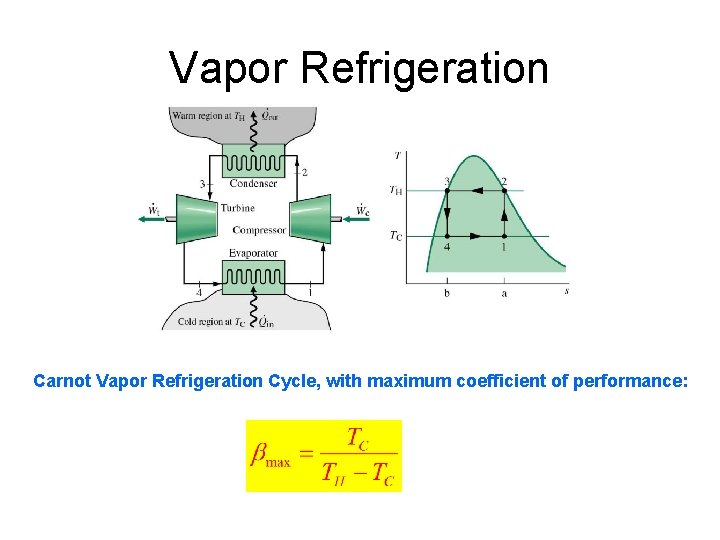
Vapor Refrigeration Carnot Vapor Refrigeration Cycle, with maximum coefficient of performance:

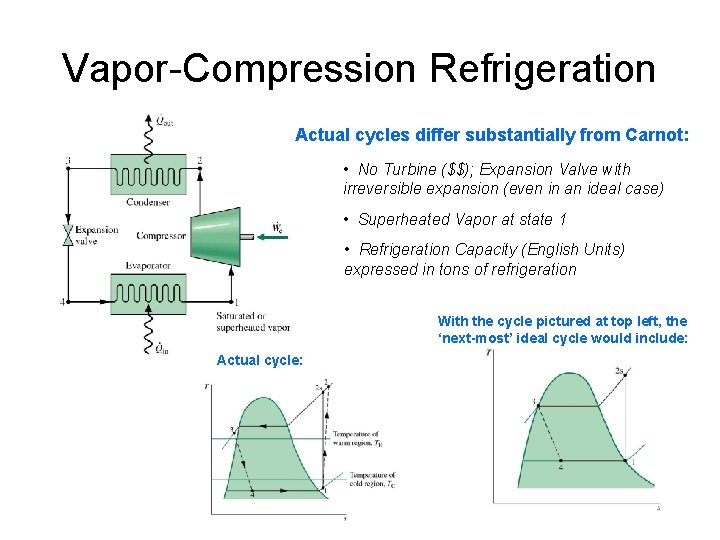
Vapor-Compression Refrigeration Actual cycles differ substantially from Carnot: • No Turbine ($$); Expansion Valve with irreversible expansion (even in an ideal case) • Superheated Vapor at state 1 • Refrigeration Capacity (English Units) expressed in tons of refrigeration With the cycle pictured at top left, the ‘next-most’ ideal cycle would include: Actual cycle:

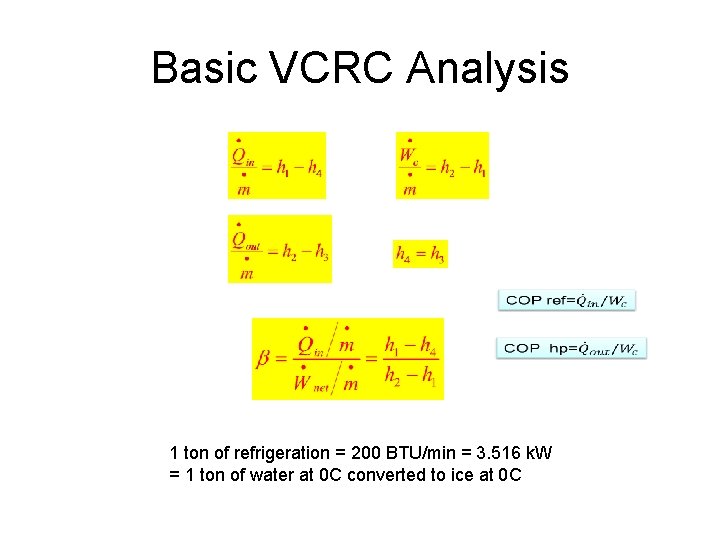
Basic VCRC Analysis 1 ton of refrigeration = 200 BTU/min = 3. 516 k. W = 1 ton of water at 0 C converted to ice at 0 C

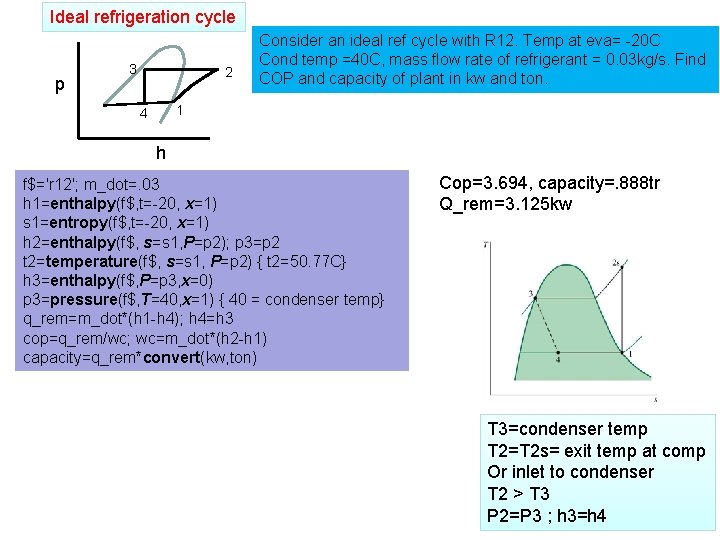
Ideal refrigeration cycle p 3 2 Consider an ideal ref cycle with R 12. Temp at eva= -20 C Cond temp =40 C, mass flow rate of refrigerant = 0. 03 kg/s. Find COP and capacity of plant in kw and ton. 1 4 h f$='r 12'; m_dot=. 03 h 1=enthalpy(f$, t=-20, x=1) s 1=entropy(f$, t=-20, x=1) h 2=enthalpy(f$, s=s 1, P=p 2); p 3=p 2 t 2=temperature(f$, s=s 1, P=p 2) { t 2=50. 77 C} h 3=enthalpy(f$, P=p 3, x=0) p 3=pressure(f$, T=40, x=1) { 40 = condenser temp} q_rem=m_dot*(h 1 -h 4); h 4=h 3 cop=q_rem/wc; wc=m_dot*(h 2 -h 1) capacity=q_rem*convert(kw, ton) Cop=3. 694, capacity=. 888 tr Q_rem=3. 125 kw T 3=condenser temp T 2=T 2 s= exit temp at comp Or inlet to condenser T 2 > T 3 P 2=P 3 ; h 3=h 4

Stirling Cycle module work(v 1, v 2, t 1: w) w=integral(pressure(air, t=t 1, v=v), v, v 1, v 2) end p 1=100; t 1=5; rk=6; t 3=400 v 1=volume(air, p=p 1, t=t 1) v 2=v 1/rk call work(v 1, v 2, t 1: w 12) q 23=u 3 -u 2; q 12=w 12+u 2 -u 1; u 1=intenergy(air, t=t 1) u 3=intenergy(air, t=t 3); u 2=intenergy(air, t=t 2) t 2=t 1 t 4=t 3 v 3=v 2; v 4=v 1 call work(v 3, v 4, t 3: w 34) q 34=w 34+u 4 -u 3 u 4=intenergy(air, t=t 4); q 41=u 1 -u 4 w_net=q 12+q 23+q 34+q 41 { w_net should equal w_comp} eff=(w_comp)/(q 23+q 34); w_comp=w 12+w 34 eff_carnot=1 -(t 1+273)/(t 3+273) 3 p 2 4 1 v Eff=31. 78%, eff_car=58. 69% W_net=203. 1 k. J, q 23=292. 9 Q 34=346. 2 Consider an ideal Stirling cycle where the beginning of isothermal compression is at 100 kpa, 5 C. Comp ratio is 6 and max temp is 400 C. Compute the max pre, thermal eff and all other state points