Clculo Diferencial e Integral III Aula 10 Profa















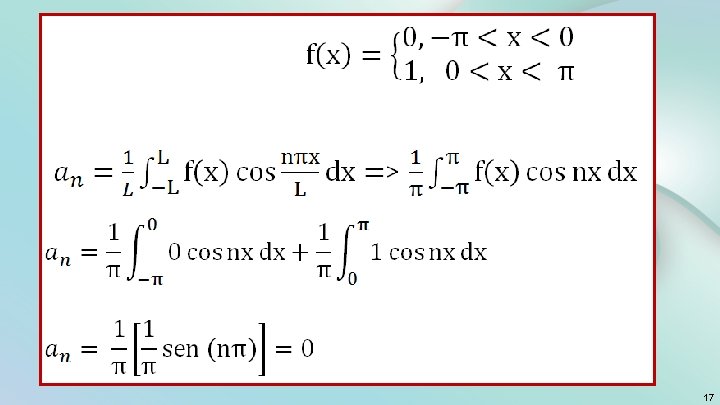


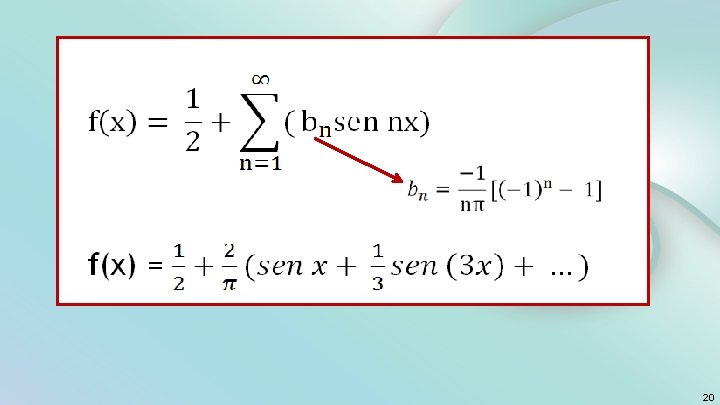









- Slides: 30

Cálculo Diferencial e Integral III Aula 10 Prof(a): Ana Lucia de Sousa

Objetivos Ø Determinar uma expansão em Série de Fourier de uma função. Ø Coeficientes na expansão em série de Fourier Ø Teorema de convergência de séries de Fourier 2

SÉRIE DE FOURIER A série de Fourier, nomeada em homenagem a Jean. Baptiste Joseph Fourier (1768 -1830). A ideia do Fourier é transformar uma função periódica numa soma infinita de senos e cossenos. 3

Funções periódicas Existem funções y = f(x) que repetem valores de y para um determinado acréscimo no valor de x. Podemos dizer que uma função f de domínio D é periódica se existe um número real P > 0, chamado período de f, tal que f(x) = f(x + P). Ou seja, a função se repete a cada período. 4

Podemos dizer que uma função f de domínio D é periódica se existe um número real P > 0, chamado período de f, tal que f(x) = f(x+P). Ou seja, a função se repete a cada período. Ou seja, função periódica é uma função que se repete a cada período. 5

Por exemplo: ØA função seno é periódica e seu período é 2π. ØA função cosseno também possui período 2π. Se f(x) tem período T, então podemos escrever f(x) = f(x + T). 6

Função par e função ímpar Uma função f é chamada de par se f(-x) = f(x) e é chamada de ímpar se f(-x) = -f(x), para todo x no domínio. Vamos entender melhor! 7

Função par: f(-x) = f(x) Isso significa que os números x e -x possuem a mesma imagem. Exemplo Seja a função f(x) = x 2 - 4 com domínio real. f(1) = -3 e f(-1) = -3, ou seja 1 e -1 possuem a mesma imagem -3. Exemplo: A função y = cosx é par, pois cos (-x) = cos x 8

Função ímpar: f(-x) = -f(x) Isso significa que os números x e -x possuem imagens opostas Exemplo Seja a função f(x) = 3 x com domínio real. f(1) = 3 e f(-1) = -3, ou seja, 1 e -1 têm imagens opostas. Exemplo: A função y = senx é ímpar, pois sen (-x) = - sen x 9

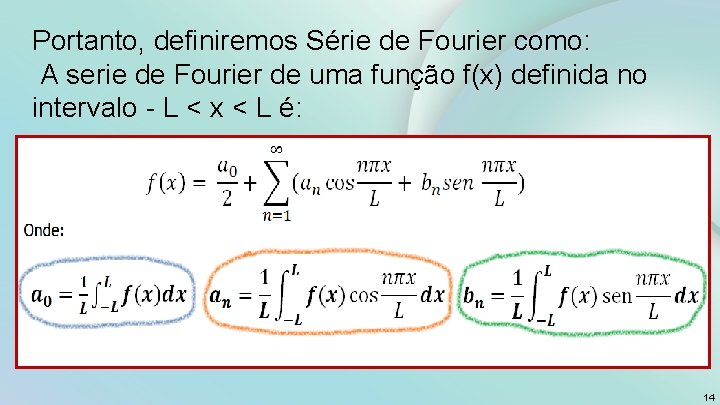
Definição: Na série de Fourier a função f(x) é escrita como uma série trigonométrica, onde f(x) é definida no intervalo – L < x < L, com período T = 2 L. 10

Chamamos a f(x) de série de Fourier. ØOs termos ao , an e bn são os coeficientes que variam dependendo da função que estamos analisando. Ø L é o período da função queremos representar como uma série. 11

Fórmula de Euler-Fourier Precisamos definir os coeficientes na expansão em série de Fourier do seguinte modo: Definindo a 0 12

Definindo an Definindo bn 13

Portanto, definiremos Série de Fourier como: A serie de Fourier de uma função f(x) definida no intervalo - L < x < L é: 14

15

16
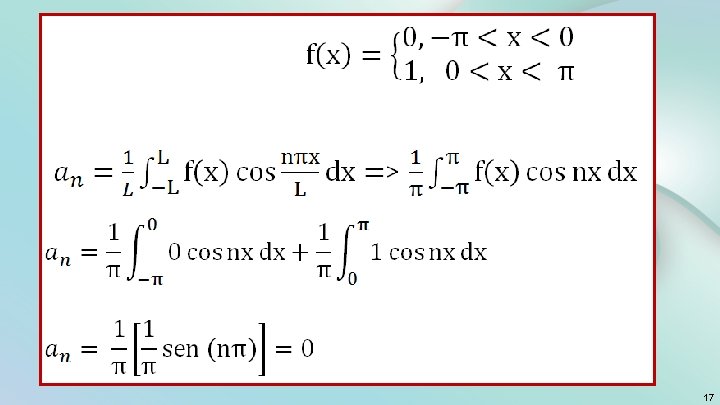
17

18

19
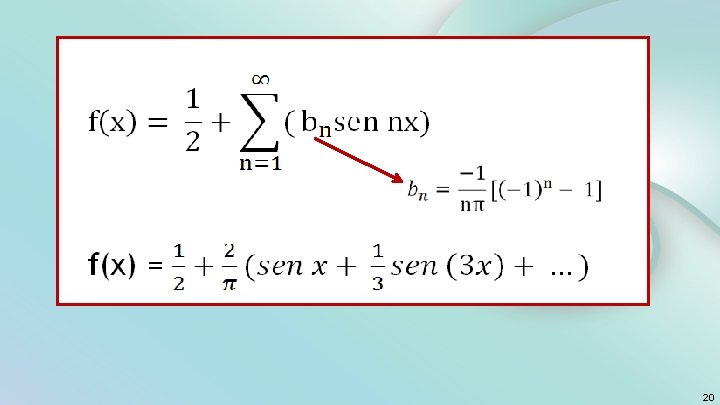
20

Øsen n = sen(-n ) = 0 Øcos (n ) = cos(-n ) = (-1)n 21

TEOREMA DE CONVERGÊNCIA DE SÉRIES DE FOURIER Se a função f e sua derivada são contínuas por partes no intervalo -L < x < L, então f é igual a sua série de Fourier em todos os pontos de continuidade. Em um ponto c onde um salto de descontinuidade ocorre em f, a série de Fourier converge para a média 22

Resumindo a convergência desta série de Fourier temos: Portanto, a série de Fourier converge para f(x) nos pontos de continuidade e para a médias dos limites laterais nos pontos de descotinuidade. 23

24

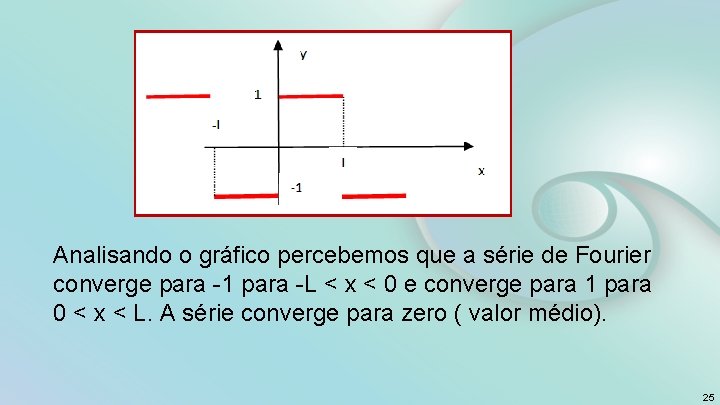
Analisando o gráfico percebemos que a série de Fourier converge para -1 para -L < x < 0 e converge para 1 para 0 < x < L. A série converge para zero ( valor médio). 25

26

27

Cálculo Diferencial e Integral III Atividade Prof(a): Ana Lucia de Sousa

29

30