Claygate Primary School Maths Mastery An overview Information

Claygate Primary School Maths Mastery- An overview Information session for parents

Aims of the session Ø Share changes in the National Curriculum in recent years Ø Give an over view of maths mastery Ø Explain changes to our teaching and learning strategies in Mathematics Ø Examples of reasoning tasks Ø Ways in which you can continue to support your children.

Changes The National Curriculum for Mathematics aims to ensure that all pupils: Ø become fluent in the fundamentals of mathematics - through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately Ø reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language Ø can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.

Maths Mastery

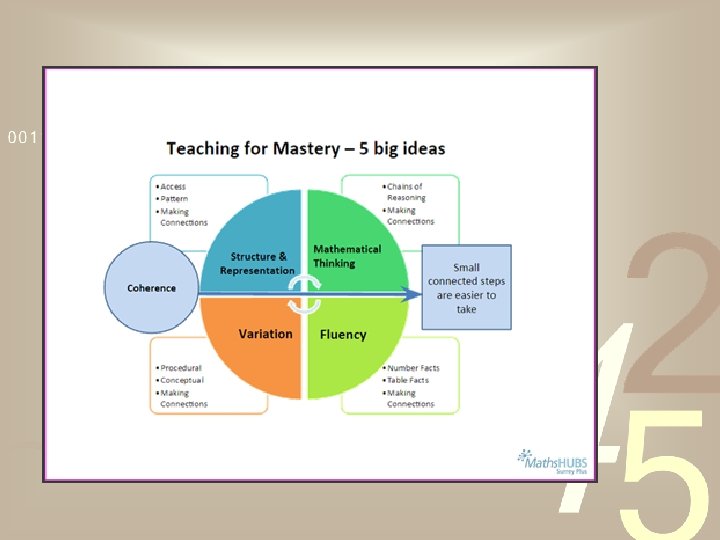
Teaching and Learning : Maths Mastery Ø An approach to teaching and learning - not a level of attainment. Ø The belief that all pupils can achieve age-appropriate targets. Ø Development of deep mathematical understanding. Ø Development of both factual/procedural and conceptual fluency. Ø Longer time spent on key topics, providing time to go deeper and embed learning rather than moving on to concepts in the next year group. Ø Loosely based on the Shanghai / Singapore style of teaching of mathematics. Ø A style of teaching that the Government is supporting.

How does it work at Claygate? Ø Each lesson is a JOURNEY- How did it begin? Where did it follow? How did it end? Ø This Journey is LOGICAL, COHERENT and CONCEPTUAL Ø DIFFERENTIATION happens through deepening understanding, not through moving on to new content so FEWER things are taught, but in GREATER DEPTH Ø Each lesson contains a REASONING element Ø Precise LANGUAGE and FULL SENTENCES are used by teachers and pupils alike Ø Sufficient time is spent on embedding KEY CONCEPTS before moving the children on Ø Groups of lessons follow a SEQUENCE so that there is a clear pathway to learning Ø Lessons are broken down into SMALL STEPS building on previous knowledge Ø TRICKY BITS and MISCONCEPTIONS can be identified in advance of the lesson so that strategies to help the children are already in place.

Mastery means that learning is sufficiently: Ø Ø Embedded Deep Connected Fluent In order for it to be: Ø Sustained Ø Built upon Ø Connected to

Coherence Ø Small steps (within a lesson, unit, year), continually building up knowledge Ø Focused, key Learning Objectives Ø Careful sequencing, building to generalisation Ø Pre-empting misconceptions Ø Opportunities for Fluency, Reasoning and Problem Solving with each objective.

Concrete- Pictorial-Abstract Approach • Reinforcement is achieved by going back and forth between these representations. Concrete- The DOING • A child is first introduced to an idea or a skill by acting it out with real objects. This is a 'hands on' component using real objects and it is the foundation for conceptual understanding. Pictorial-The SEEING • A child has sufficiently understood the hands-on experiences performed and can now relate them to representations, such as a diagram or picture of the problem. Abstract – The SYMBOLIC • A child is now capable of representing problems by using mathematical notation, for example: 12 ÷ 2 = 6

Partner Work Ø Children share their ideas and partners can learn from each other Ø Partner work ensures good Mathematical discussions and ‘bouncing’ of ideas Ø Children practise new vocabulary in full sentences Ø Children check each other’s working and make corrections Ø Children have a shared experience of maths – all feel successful in their learning.

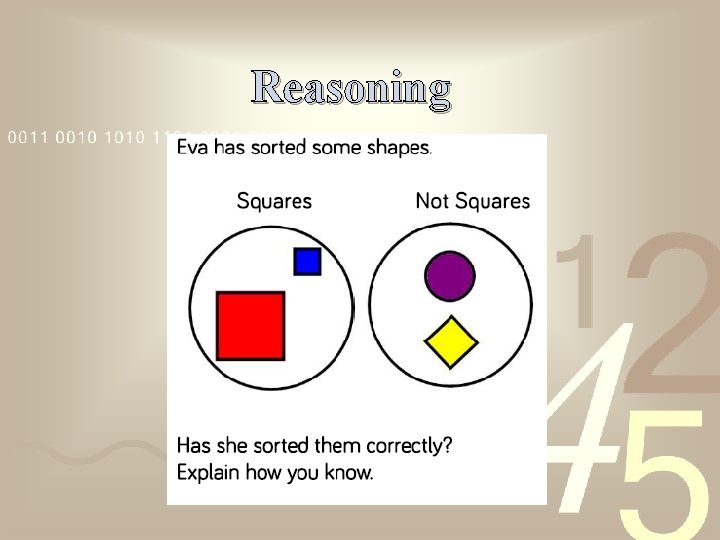
Reasoning

Which number is the odd one out? Explain your answer. 13 17 10 25

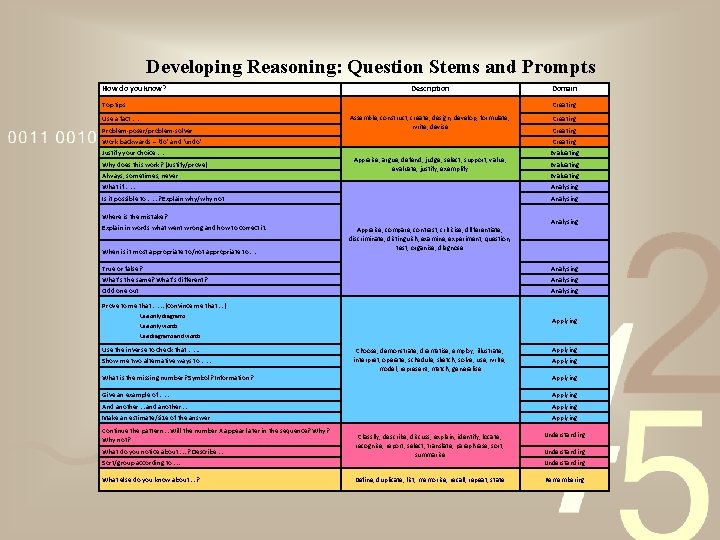
Developing Reasoning: Question Stems and Prompts How do you know? Description Top tips Domain Creating Use a fact…… Problem-poser/problem-solver Assemble, construct, create, design, develop, formulate, write, devise Work backwards – ‘do’ and ‘undo’ Justify your choice…… Why does this work? (Justify/prove) Always, sometimes, never Creating Appraise, argue, defend, judge, select, support, value, evaluate, justify, exemplify Evaluating What if……. Analysing Is it possible to……. ? Explain why/why not Analysing Where is the mistake? Explain in words what went wrong and how to correct it. When is it most appropriate to/not appropriate to…… Appraise, compare, contrast, criticise, differentiate, discriminate, distinguish, examine, experiment, question, test, organise, diagnose Analysing True or false? Analysing What’s the same? What’s different? Analysing Odd one out Analysing Prove to me that……. . (convince me that…. ) Use only diagrams Applying Use only words Use diagrams and words Use the inverse to check that……. . Show me two alternative ways to……. Choose, demonstrate, dramatise, employ, illustrate, interpret, operate, schedule, sketch, solve, use, write, model, represent, match, generalise Applying What is the missing number? Symbol? Information? Applying Give an example of……. Applying And another…. and another…. Applying Make an estimate/size of the answer Applying Continue the pattern…. Will the number X appear later in the sequence? Why not? What do you notice about…. . ? Describe…. Sort/group according to…. . What else do you know about…. ? Classify, describe, discuss, explain, identify, locate, recognise, report, select, translate, paraphrase, sort, summarise Understanding Define, duplicate, list, memorise, recall, repeat, state Remembering Understanding

And finally…

Supporting your child at home v Give your child concrete resources when solving problems e. g counters, objects, cars, fruit, socks v Ask your child to prove it, explain, convince me both verbally and through pictorial/written representations v Refer to the school website for End of Year expectations v Continue to reinforce mental maths strategies v Support your child becoming fluent in their times tables up to 12, using ‘Times Tables Rockstars’ v Where possible link maths to real life e. g cooking, shopping, telling the time

Ideas Use real-life contexts Ø Make the most of shopping trips and other outings- talk about spending money and calculating change. Does your child understand the offers they see on signs or adverts in shops? Ø Maths is a broad subject and encompasses topics like measure and shape- Can your child recognise shapes in their everyday surroundings? Can they tell the time? Or use weighing scales? Ø Think about how you can involve your child in everyday problem solving. You may be planning a party or cooking dinner. Many tasks involve sharing or using fractions.