Classroom Simulation Are VarianceStabilizing Transformations Really Useful Trumbo

Classroom Simulation: Are Variance-Stabilizing Transformations Really Useful?

* Trumbo Bruce E. Eric A. Suess † Rebecca E. Brafman Department of Statistics California State University, Hayward † Presentation, JSM 2004, Toronto * btrumbo@csuhayward. edu

Introduction to One-way ANOVA In a one-way ANOVA, we test the null hypothesis that all group means i are equal against the alternative hypotheses that all group means are not equal. ANOVA Table Source DF SS MS F-Ratio . Factor I – 1 SS(Fact) MS(Fact)/MS(Err) Error IJ – I SS(Err) MS(Err). Total IJ – 1

Model and Assumptions We use the model: Xij i. i. d. NORM( i, 2), for i = 1, …, I and j = 1, …, J. Assumptions: – normal data – independent groups – independent observations within groups – equal variances

When Data Are Not Normal… • If H 0 True: Distributional difficulties arise – MS(Factor) and MS(Error) not chi-squared – MS(Factor) and MS(Error) not independent – F-ratio not distributed as F • If H 0 False: – Different means may imply – Different variances

Commonly Recommended Method For Transformating Data to Stabilize Variances Based on two-term Taylor-series approximations. Given relationship between mean and variance: 2 = j( ). The following transformation makes variances approximately equal — even if means differ: Y = f(X), where f’( ) = [j( )]– 1/2

Some Types of Nonnormal Data and Their Variance-Stabilizing Transformations Type of Relationship of Distribution Mean & Variance Poisson Variance = Mean Type of Transformation Square Root Binomial Mean = p Proportions Variance = p(1–p)/n Exponential SD = Mean Arcsine of Square Root Log and Rank

Square Root Transformations (Right) of Three Poisson Samples Have Similar Variances

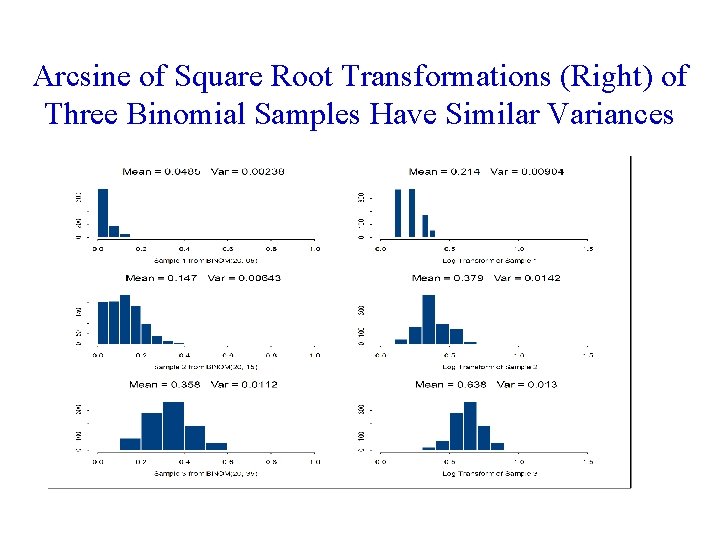
Arcsine of Square Root Transformations (Right) of Three Binomial Samples Have Similar Variances

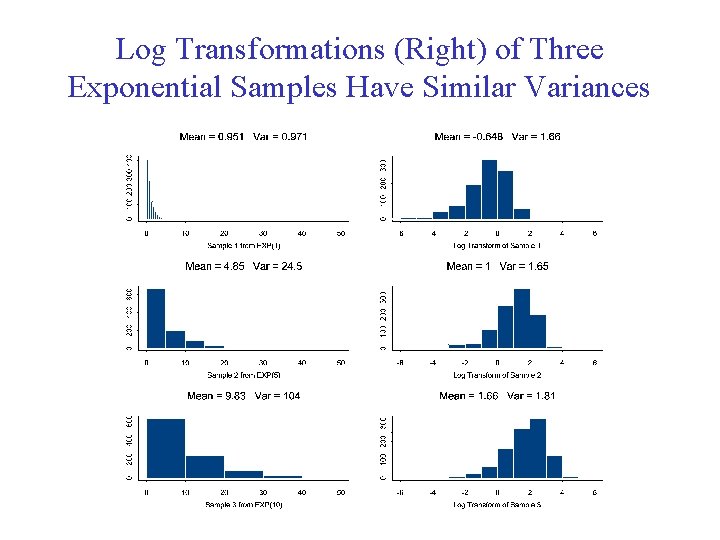
Log Transformations (Right) of Three Exponential Samples Have Similar Variances

Additional Transformations We also consider rank transformations for exponential data. Possible future work (no results given here): Box-Cox Transformation of the type Y = Xa, where a is based on the data. Examples: • Square root if a = 1/2 • Reciprocal if a = – 1 • Interpreted as log transformation if a = 0

Simulation Study 1. Simulations are based on data with known distributions: Poisson, binomial, or exponential. 2. Use R, S-Plus, and Minitab. (SAS can also be used but is very time consuming. ) 3. In each simulation we generate 20, 000 datasets from the nonnormal distribution under study. 4. Each dataset consists of I = 3 groups, usually with J = 5 or 10 observations per group. 5. For each distribution: Datasets under H 0, and for a variety of cases with Ha.

Comparisons to Judge Usefulness of Transformations All tests have nominal size = 5%. P{Rej} is estimated as the proportion of 20, 000 simulated datasets in which H 0 is rejected. With and without transformation: When is H 0 is true, does P{Rej} = 5% ? For various alternatives: When is P{Rej} larger, with or without transformation?

R / S-Plus Code for Exponential Simulation

Summary of Findings Within the limited scope of our study… For Poisson data, the square root transformation seems ineffective. For binomial data, the “arcsine” transformation seems ineffective. For exponential data, both the log and the rank transformations seem to be useful in some cases—particularly for small samples.

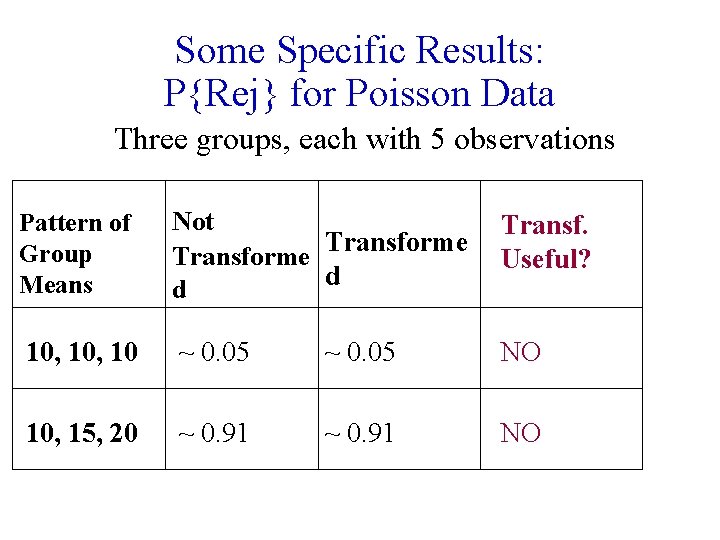
Some Specific Results: P{Rej} for Poisson Data Three groups, each with 5 observations Pattern of Group Means Not Transforme d d Transf. Useful? 10, 10 ~ 0. 05 NO 10, 15, 20 ~ 0. 91 NO

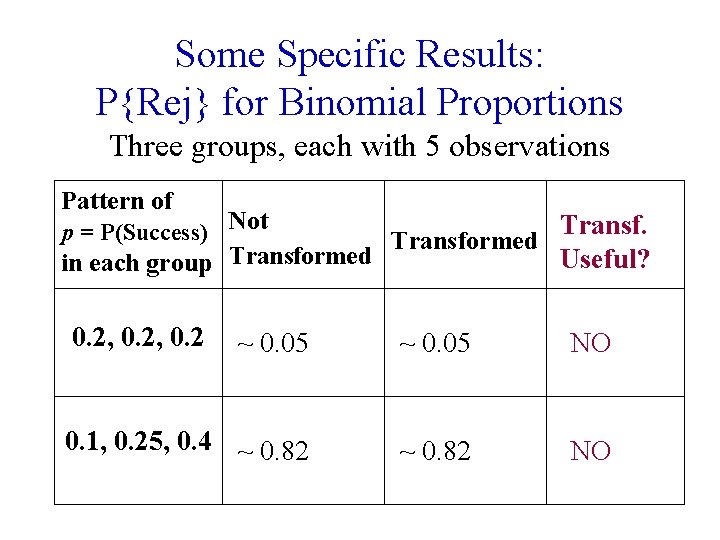
Some Specific Results: P{Rej} for Binomial Proportions Three groups, each with 5 observations Pattern of Transf. p = P(Success) Not Transformed Useful? in each group 0. 2, 0. 2 ~ 0. 05 NO 0. 1, 0. 25, 0. 4 ~ 0. 82 NO

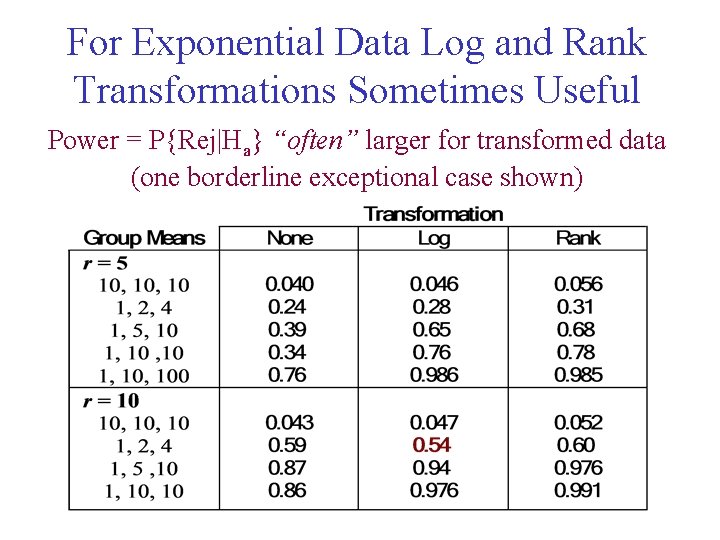
For Exponential Data Log and Rank Transformations Sometimes Useful Power = P{Rej|Ha} “often” larger for transformed data (one borderline exceptional case shown)

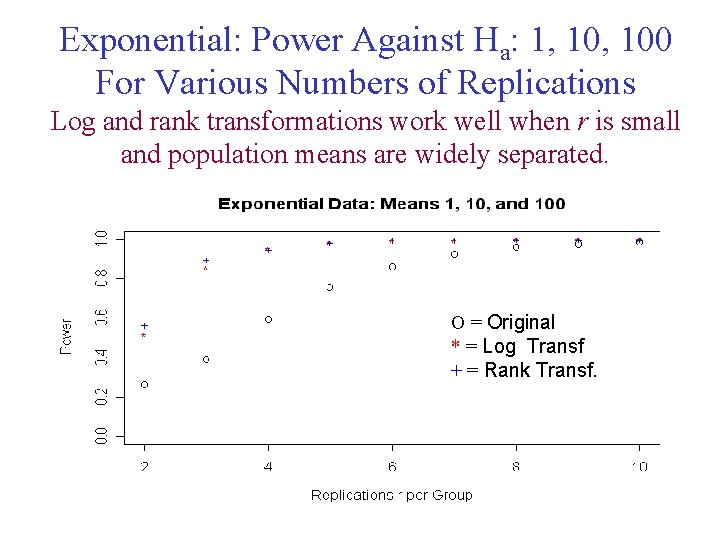
Exponential: Power Against Ha: 1, 100 For Various Numbers of Replications Log and rank transformations work well when r is small and population means are widely separated. O = Original * = Log Transf + = Rank Transf.

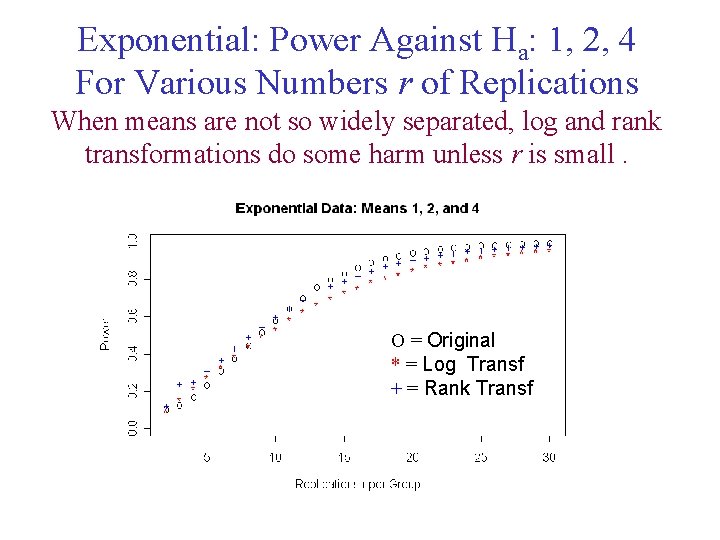
Exponential: Power Against Ha: 1, 2, 4 For Various Numbers r of Replications When means are not so widely separated, log and rank transformations do some harm unless r is small. O = Original * = Log Transf + = Rank Transf .

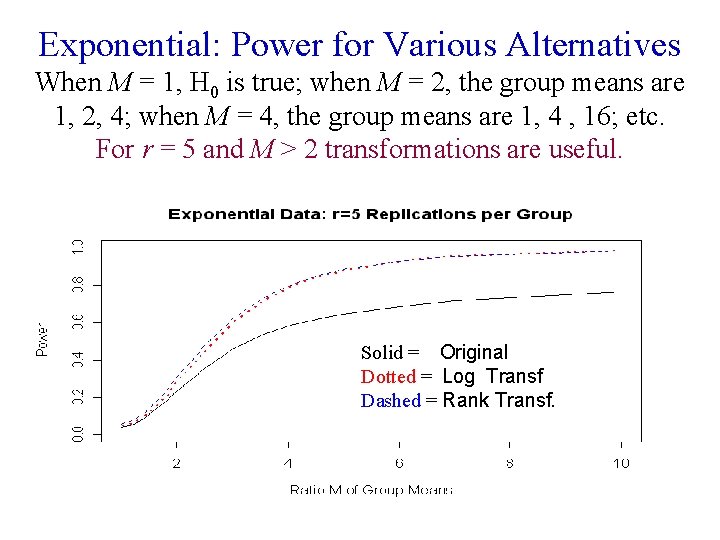
Exponential: Power for Various Alternatives When M = 1, H 0 is true; when M = 2, the group means are 1, 2, 4; when M = 4, the group means are 1, 4 , 16; etc. For r = 5 and M > 2 transformations are useful. Solid = Original Dotted = Log Transf Dashed = Rank Transf.

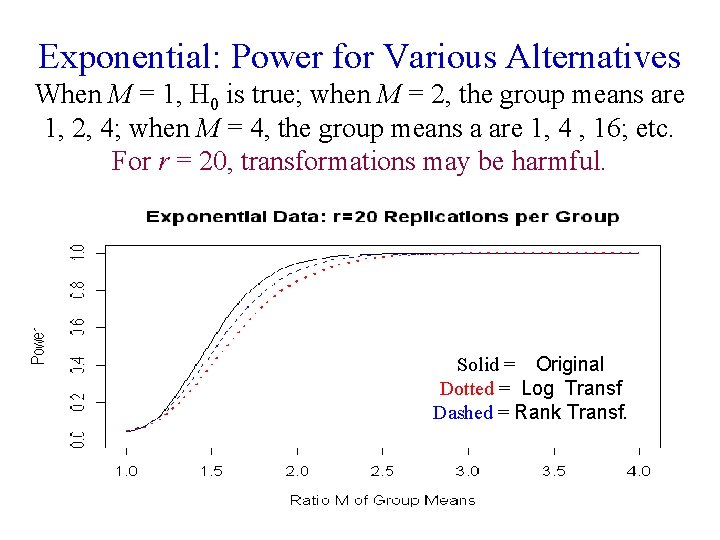
Exponential: Power for Various Alternatives When M = 1, H 0 is true; when M = 2, the group means are 1, 2, 4; when M = 4, the group means a are 1, 4 , 16; etc. For r = 20, transformations may be harmful. Solid = Original Dotted = Log Transf Dashed = Rank Transf.

References / Acknowledgments REFERENCES ON VARIANCE STABILIZING TRANSFORMATIONS G. Oehlert: A First Course in Design and Analysis of Experiments, Freeman (2000), Chapter 6. D. Montgomery: Design and Analysis of Experiments, 5 th ed. , Wiley (2001), Chapter 3. K. Brownlee: Statistical Theory and Methodology in Science and Engineering, 2 nd ed. , Wiley (1965). Chapter 3. H. Scheffé: The Analysis of Variance, Wiley 1959, Chapter 10. G. Snedecor and W. Cochran: Statistical Methods, 7 th ed. Iowa State Univ. Press (1980), Chapter 15. WEB PAGES including computer code and results for this paper: www. sci. csuhayward. edu/~btrumbo/JSM 2004/simtrans/. THANKS TO Jaimyoung Kwan (UC Berkeley/CSU Hayward) for suggestions, especially concerning the inclusion of power curves. Rebecca Brafman’s graduate study supported by NSF Graduate Research Fellowship.

About the Authors • Rebecca E. Brafman, presenting this poster at JSM 2004 in Toronto, has recently completed her M. S. in Statistics from CSU Hayward. • Eric A. Suess received his Ph. D. in Statistics from U. C. Davis and is Associate Professor of Statistics at CSU Hayward. His interests include statistical computation, time series and Bayesian statistics. esuess@csuhayward. edu • Bruce E. Trumbo is a fellow of ASA and IMS and has been a professor in the Statistics Department at CSU State University, Hayward for over 30 years. btrumbo@csuhayward. edu