CLASSIFYING POLYNOMIALS Todays Objectives Classify a polynomial by

CLASSIFYING POLYNOMIALS

Today’s Objectives: Ø Ø Ø Classify a polynomial by it’s degree. Classify a polynomial by it’s number of terms “Name” a polynomial by it’s “first and last names” determined by it’s degree and number of terms.

Degree of a Polynomial The degree of a polynomial is calculated by finding the largest exponent in the polynomial.

Degree of a Polynomial (Each degree has a special “name”) 9

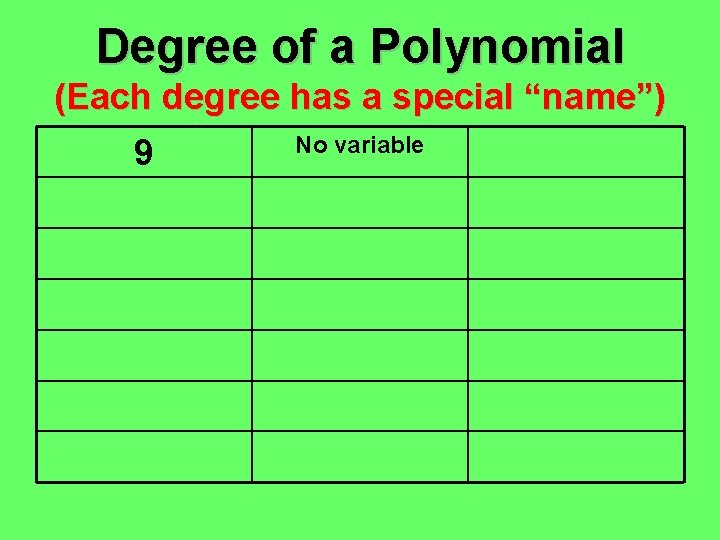
Degree of a Polynomial (Each degree has a special “name”) 9 No variable

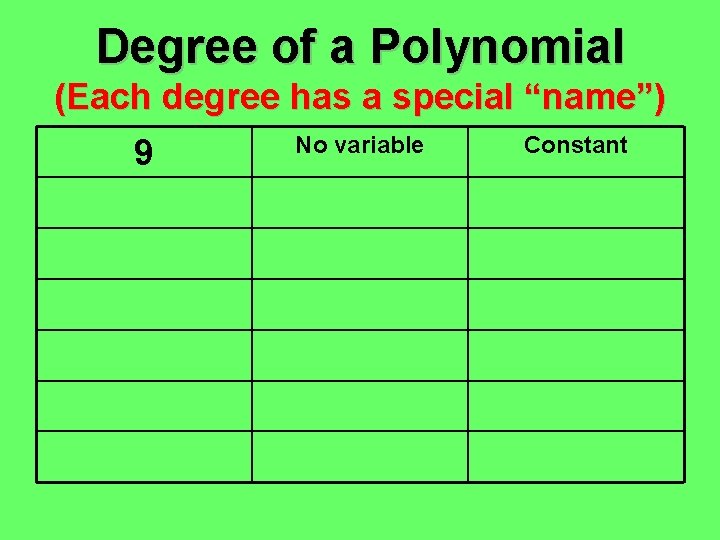
Degree of a Polynomial (Each degree has a special “name”) 9 No variable Constant

Degree of a Polynomial (Each degree has a special “name”) 9 8 x No variable Constant

Degree of a Polynomial (Each degree has a special “name”) 9 8 x No variable 1 st degree Constant

Degree of a Polynomial (Each degree has a special “name”) 9 8 x No variable Constant 1 st degree Linear

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x No variable Constant 1 st degree Linear

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x No variable Constant 1 st degree Linear 2 nd degree

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x No variable Constant 1 st degree Linear 2 nd degree Quadratic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x No variable Constant 1 st degree Linear 2 nd degree Quadratic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic 4 th degree

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic 4 th degree Quartic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 2 x 5 + 7 x 3 No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic 4 th degree Quartic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 2 x 5 + 7 x 3 No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic 4 th degree Quartic 5 th degree

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 2 x 5 + 7 x 3 No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic 4 th degree Quartic 5 th degree Quintic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 2 x 5 + 7 x 3 5 xn No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic 4 th degree Quartic 5 th degree Quintic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 2 x 5 + 7 x 3 5 xn No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic 4 th degree Quartic 5 th degree Quintic “nth” degree

Degree of a Polynomial (Each degree has a special “name”) No variable Constant 9 st degree 1 Linear 8 x nd degree 2 Quadratic 2 7 x + 3 x rd degree 3 Cubic 3 6 x – 2 x th degree 4 Quartic 4 3 x + 5 x – 1 th degree 5 Quintic 5 3 2 x + 7 x “nth” degree 5 xn

Let’s practice classifying polynomials by “degree”. 1. 2. 3. 4. 5. 6. 7. 8. 9. POLYNOMIAL 3 z 4 + 5 z 3 – 7 15 a + 25 185 2 c 10 – 7 c 6 + 4 c 3 - 9 2 f 3 – 7 f 2 + 1 15 y 2 9 g 4 – 3 g + 5 10 r 5 – 7 r 16 n 7 + 6 n 4 – 3 n 2 1. 2. 3. 4. 5. 6. 7. 8. 9. DEGREE NAME Quartic Linear Constant Tenth degree Cubic Quadratic Quartic Quintic Seventh degree The degree name becomes the “first name” of the polynomial.

Naming Polynomials (by number of terms)

Naming Polynomials (by number of terms) One term

Naming Polynomials (by number of terms) One term Monomial

Naming Polynomials (by number of terms) One term Monomial

Naming Polynomials (by number of terms) One term Two terms Monomial

Naming Polynomials (by number of terms) One term Monomial Two terms Binomial

Naming Polynomials (by number of terms) One term Monomial Two terms Binomial

Naming Polynomials (by number of terms) One term Monomial Two terms Binomial Three terms

Naming Polynomials (by number of terms) One term Monomial Two terms Binomial Three terms Trinomial

Naming Polynomials (by number of terms) One term Monomial Two terms Binomial Three terms Trinomial

Naming Polynomials (by number of terms) One term Monomial Two terms Binomial Three terms Trinomial Four (or more) terms

Naming Polynomials (by number of terms) One term Monomial Two terms Binomial Three terms Trinomial Four (or more) Polynomial with 4 (or more) terms

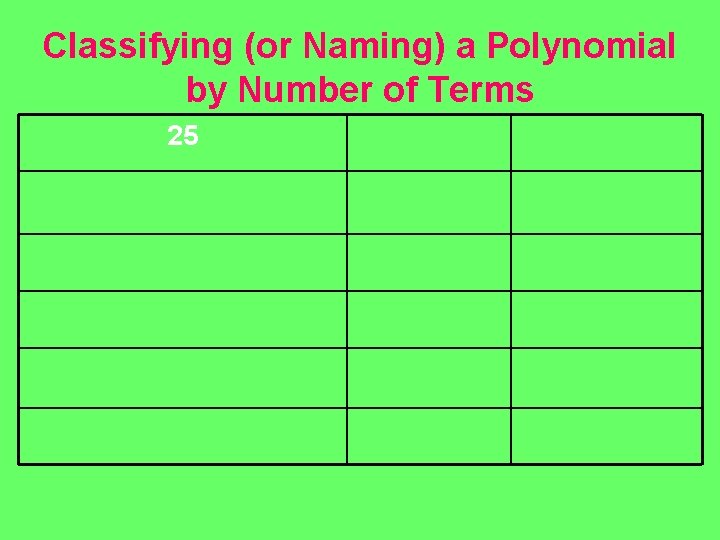
Classifying (or Naming) a Polynomial by Number of Terms 25

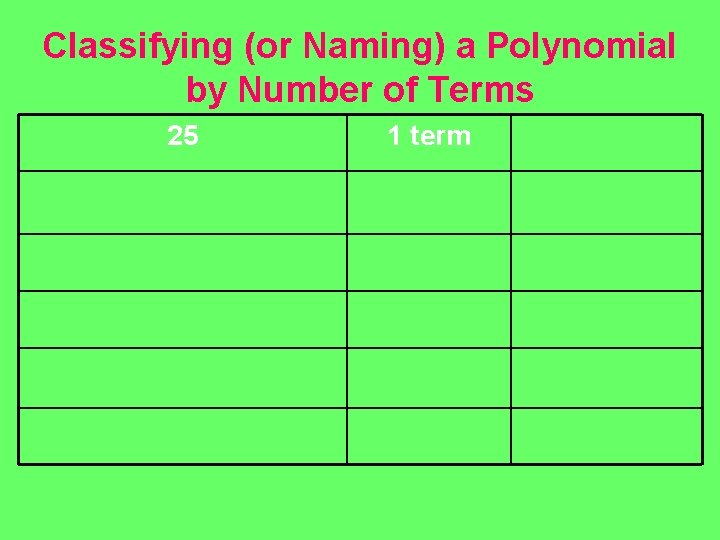
Classifying (or Naming) a Polynomial by Number of Terms 25 1 term

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial

Classifying (or Naming) a Polynomial by Number of Terms 25 15 h 1 term Monomial

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term 15 h 1 term Monomial

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms Binomial

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms Binomial 3 t 7 – 4 t 6 + 12

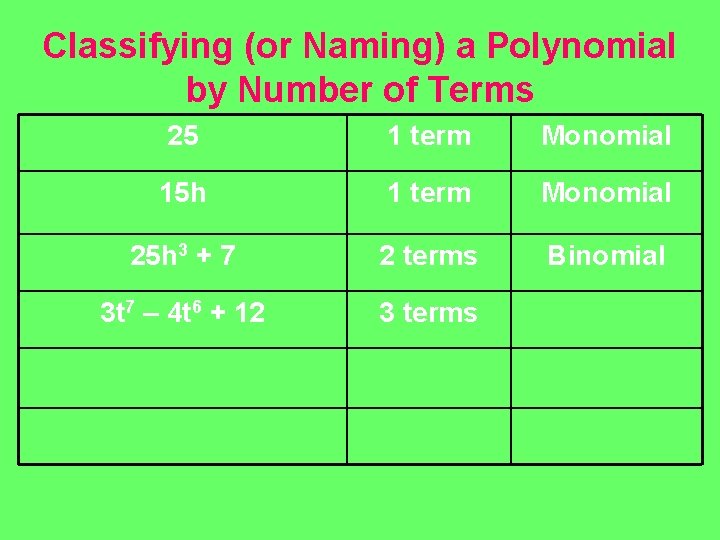
Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms Binomial 3 t 7 – 4 t 6 + 12 3 terms

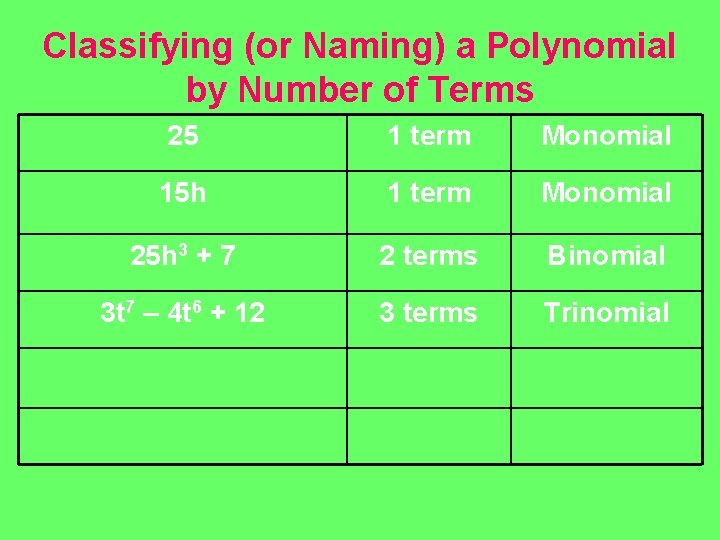
Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms Binomial 3 t 7 – 4 t 6 + 12 3 terms Trinomial

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms Binomial 3 t 7 – 4 t 6 + 12 3 terms Trinomial 4 b 10 + 2 b 8 – 7 b 6 - 8

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms Binomial 3 t 7 – 4 t 6 + 12 3 terms Trinomial 4 b 10 + 2 b 8 – 7 b 6 - 8 4 (or more) terms

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms Binomial 3 t 7 – 4 t 6 + 12 3 terms Trinomial 4 b 10 + 2 b 8 – 7 b 6 - 8 4 (or more) terms Polynomial with 4 terms

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms Binomial 3 t 7 – 4 t 6 + 12 3 terms Trinomial 4 b 10 + 2 b 8 – 7 b 6 - 8 4 (or more) terms Polynomial with 4 terms 8 j 7 – 3 j 5 + 2 j 4 - j 2 - 6 j + 7

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms Binomial 3 t 7 – 4 t 6 + 12 3 terms Trinomial 4 b 10 + 2 b 8 – 7 b 6 - 8 4 (or more) terms Polynomial with 4 terms 8 j 7 – 3 j 5 + 2 j 4 - j 2 - 6 j + 7 6 terms

Classifying (or Naming) a Polynomial by Number of Terms 25 1 term Monomial 15 h 1 term Monomial 25 h 3 + 7 2 terms Binomial 3 t 7 – 4 t 6 + 12 3 terms Trinomial 4 b 10 + 2 b 8 – 7 b 6 - 8 4 (or more) terms Polynomial with 4 terms Polynomial with 6 terms The term name becomes the “last name” of a polynomial. 8 j 7 – 3 j 5 + 2 j 4 - j 2 - 6 j + 7 6 terms

Let’s practice classifying a polynomial by “number of terms”. Polynomial 1. 2. 3. 4. 5. 6. 7. 8. Classify by # of Terms: 1. Monomial 15 x 2. 2 e 8 – 3 e 7 + 3 e – 7 3. 6 c + 5 4. 3 y 7 – 4 y 5 + 8 y 3 5. 64 2 p 8 – 4 p 6 + 9 p 4 + 3 p – 1 6. 7. 25 h 3 – 15 h 2 + 18 8. 55 c 19 + 35 Polynomial with 4 terms Binomial Trinomial Monomial Polynomial with 5 terms Trinomial Binomial

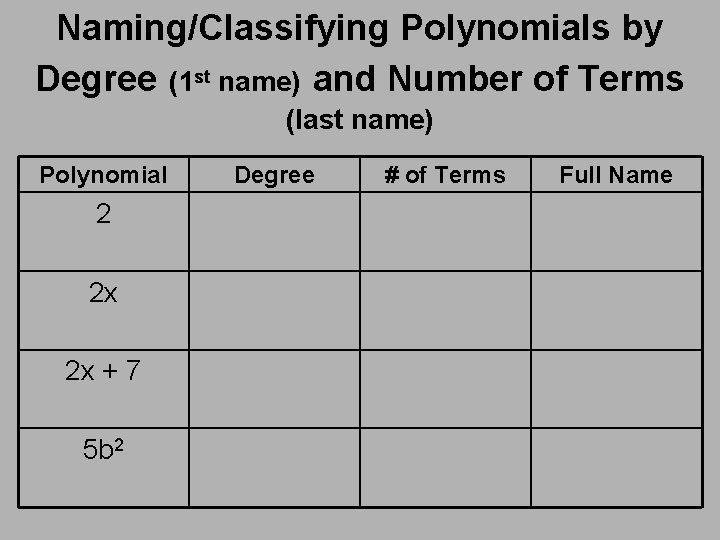
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial 2 2 x 2 x + 7 5 b 2 Degree # of Terms Full Name

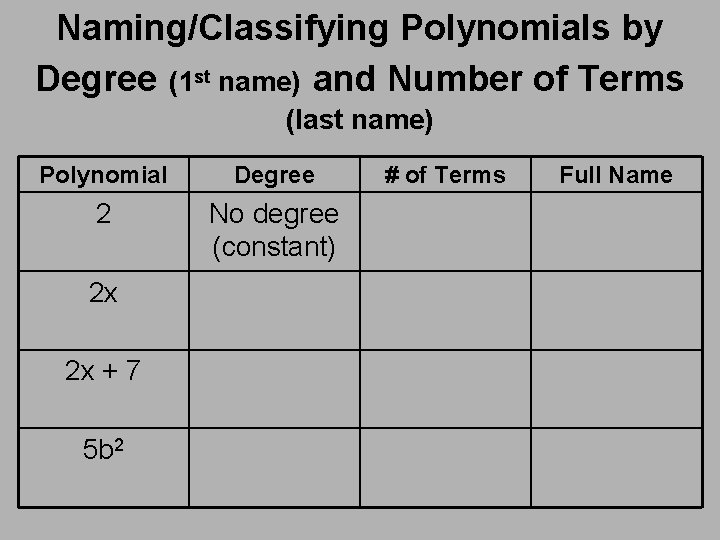
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree 2 No degree (constant) 2 x 2 x + 7 5 b 2 # of Terms Full Name

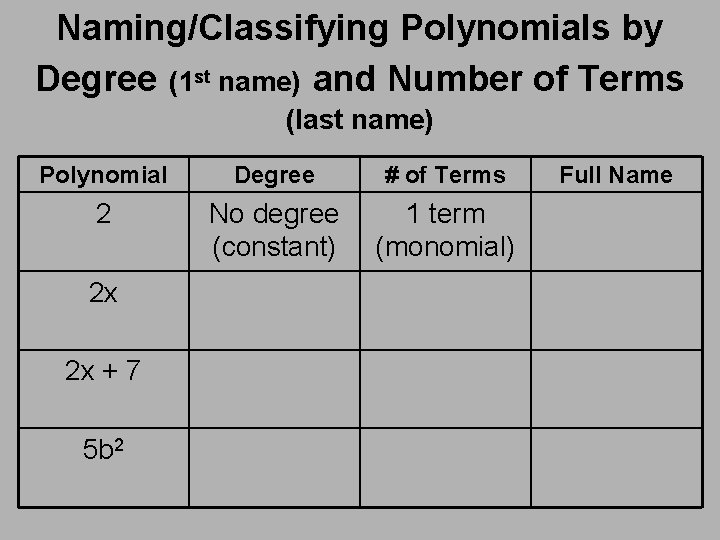
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree # of Terms 2 No degree (constant) 1 term (monomial) 2 x 2 x + 7 5 b 2 Full Name

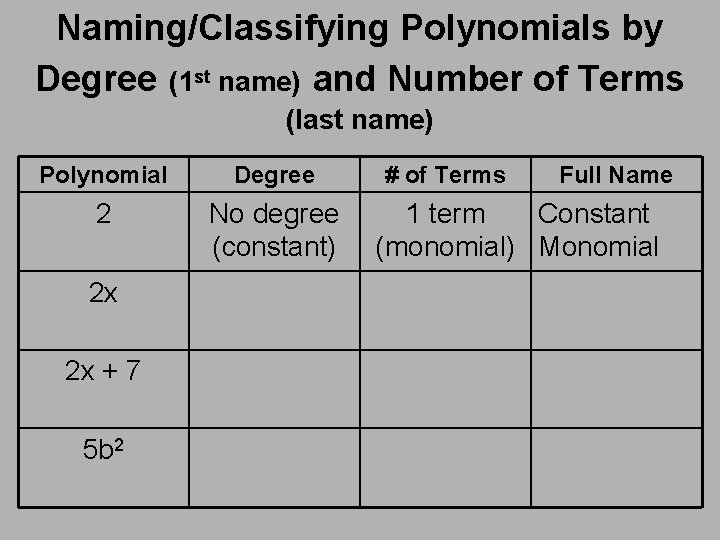
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree 2 No degree (constant) 2 x 2 x + 7 5 b 2 # of Terms Full Name 1 term Constant (monomial) Monomial

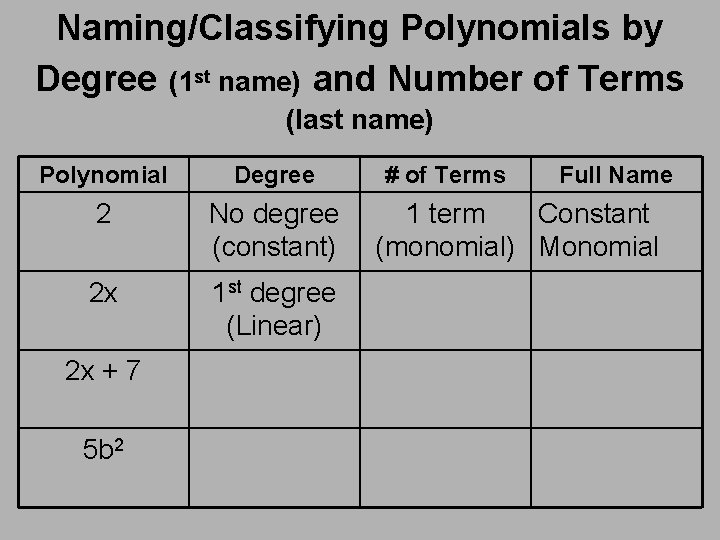
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree 2 No degree (constant) 2 x 1 st degree (Linear) 2 x + 7 5 b 2 # of Terms Full Name 1 term Constant (monomial) Monomial

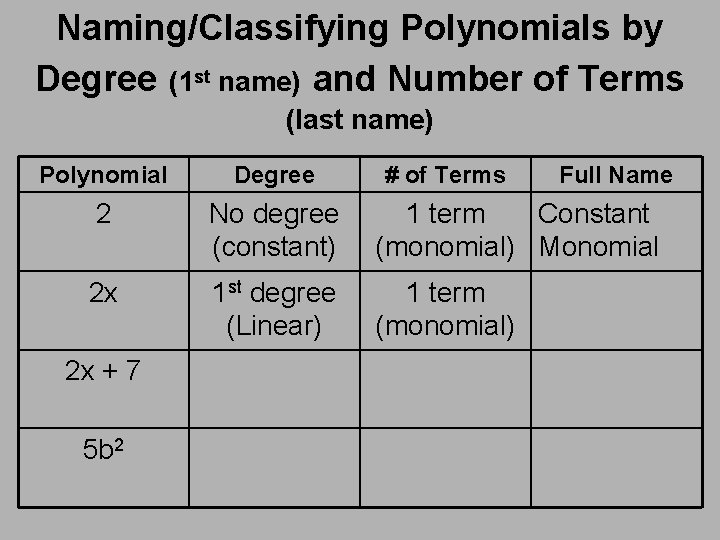
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree 2 No degree (constant) 1 term Constant (monomial) Monomial 2 x 1 st degree (Linear) 1 term (monomial) 2 x + 7 5 b 2 # of Terms Full Name

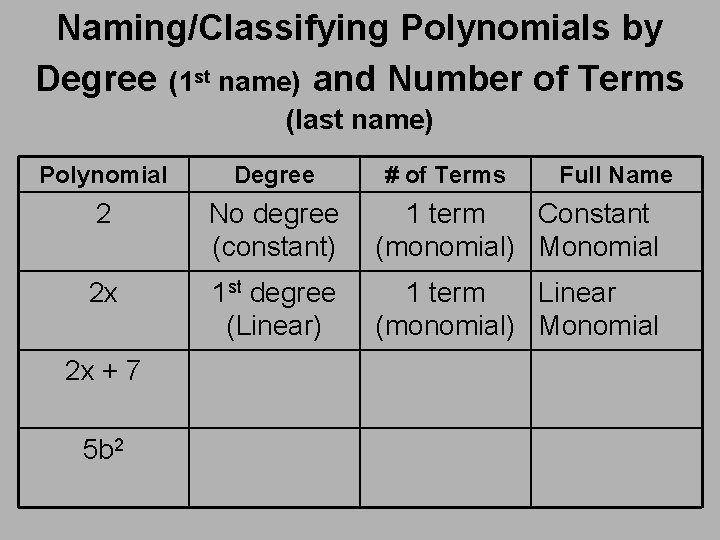
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree 2 No degree (constant) 1 term Constant (monomial) Monomial 2 x 1 st degree (Linear) 1 term Linear (monomial) Monomial 2 x + 7 5 b 2 # of Terms Full Name

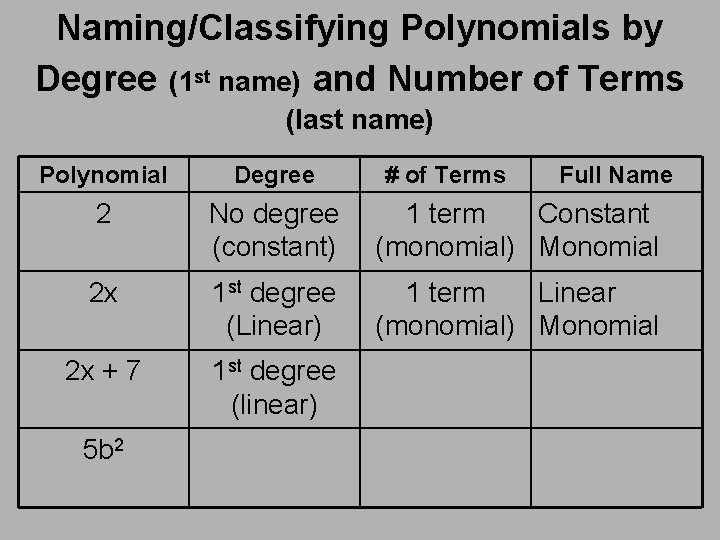
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree 2 No degree (constant) 1 term Constant (monomial) Monomial 2 x 1 st degree (Linear) 1 term Linear (monomial) Monomial 2 x + 7 1 st degree (linear) 5 b 2 # of Terms Full Name

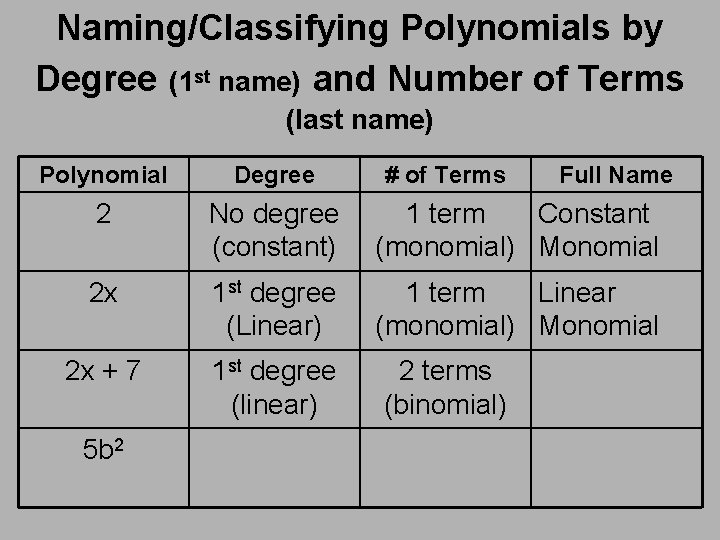
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree 2 No degree (constant) 1 term Constant (monomial) Monomial 2 x 1 st degree (Linear) 1 term Linear (monomial) Monomial 2 x + 7 1 st degree (linear) 5 b 2 # of Terms 2 terms (binomial) Full Name

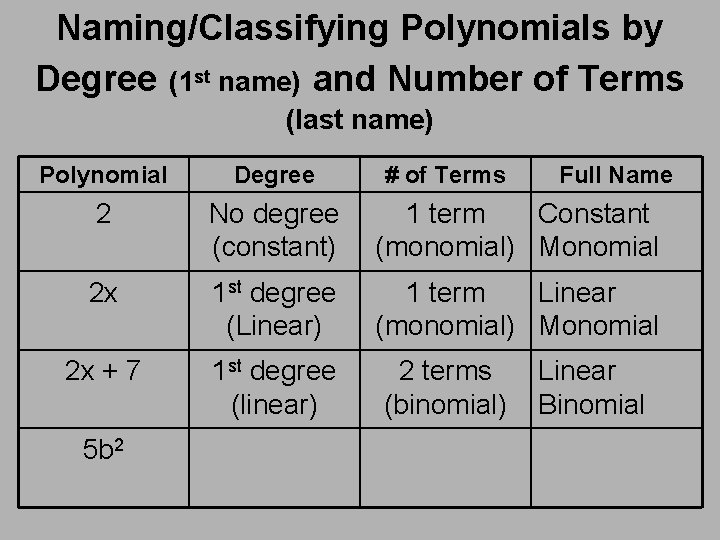
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree 2 No degree (constant) 1 term Constant (monomial) Monomial 2 x 1 st degree (Linear) 1 term Linear (monomial) Monomial 2 x + 7 1 st degree (linear) 5 b 2 # of Terms 2 terms (binomial) Full Name Linear Binomial

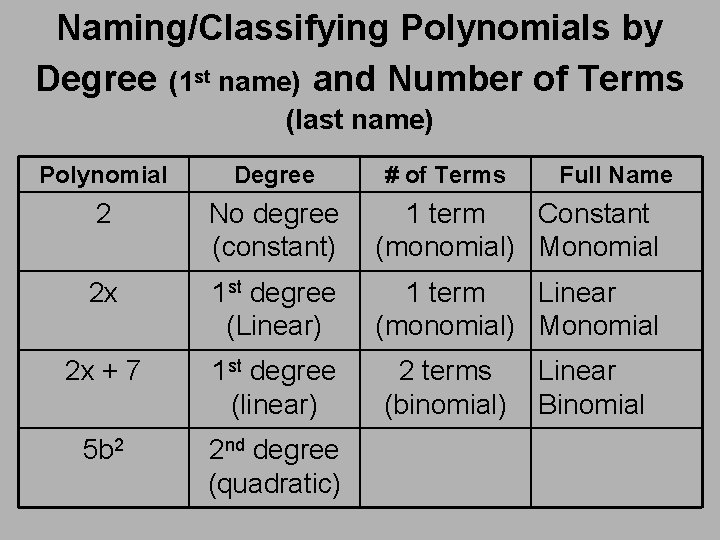
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree # of Terms 2 No degree (constant) 1 term Constant (monomial) Monomial 2 x 1 st degree (Linear) 1 term Linear (monomial) Monomial 2 x + 7 1 st degree (linear) 5 b 2 2 nd degree (quadratic) 2 terms (binomial) Full Name Linear Binomial

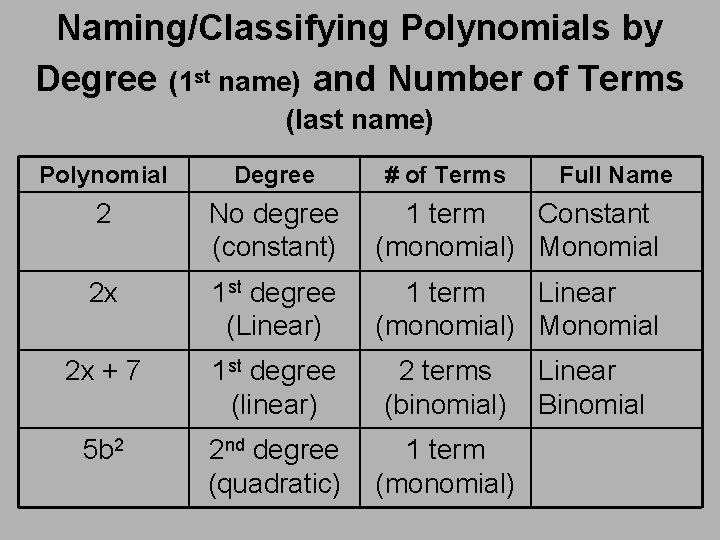
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree # of Terms Full Name 2 No degree (constant) 1 term Constant (monomial) Monomial 2 x 1 st degree (Linear) 1 term Linear (monomial) Monomial 2 x + 7 1 st degree (linear) 2 terms (binomial) 5 b 2 2 nd degree (quadratic) 1 term (monomial) Linear Binomial

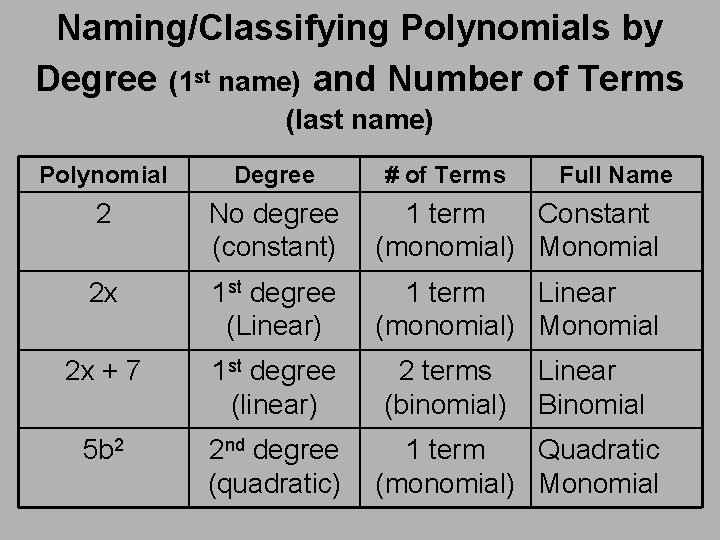
Naming/Classifying Polynomials by Degree (1 st name) and Number of Terms (last name) Polynomial Degree # of Terms 2 No degree (constant) 1 term Constant (monomial) Monomial 2 x 1 st degree (Linear) 1 term Linear (monomial) Monomial 2 x + 7 1 st degree (linear) 5 b 2 2 nd degree (quadratic) 2 terms (binomial) Full Name Linear Binomial 1 term Quadratic (monomial) Monomial

. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4

. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic)

. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 2 terms (binomial)

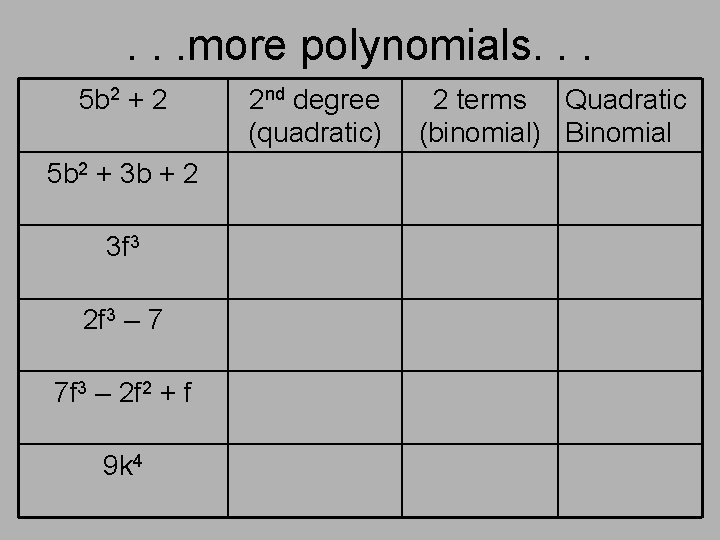
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 2 terms Quadratic (binomial) Binomial

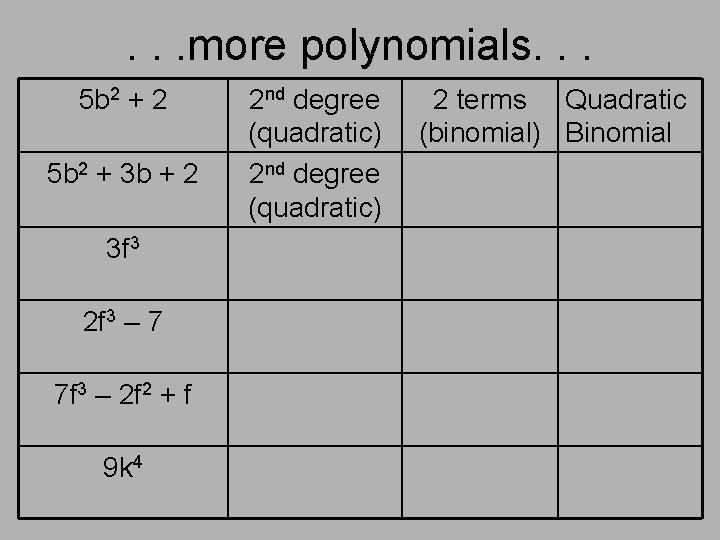
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 2 terms Quadratic (binomial) Binomial

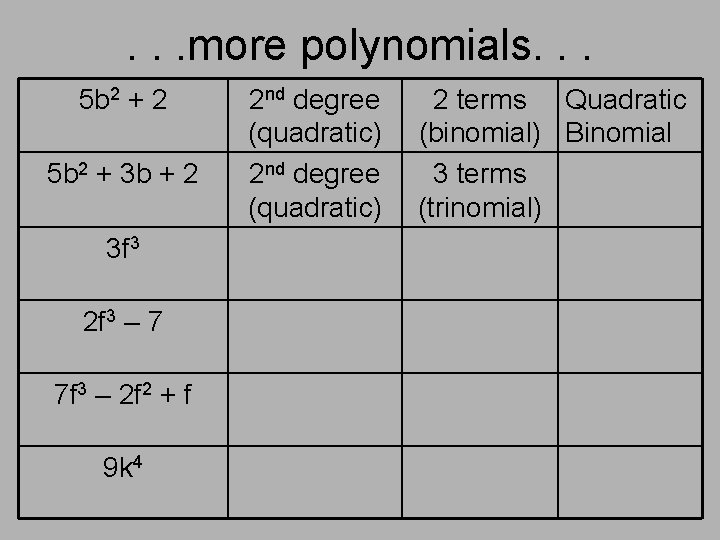
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 2 terms Quadratic (binomial) Binomial 3 terms (trinomial)

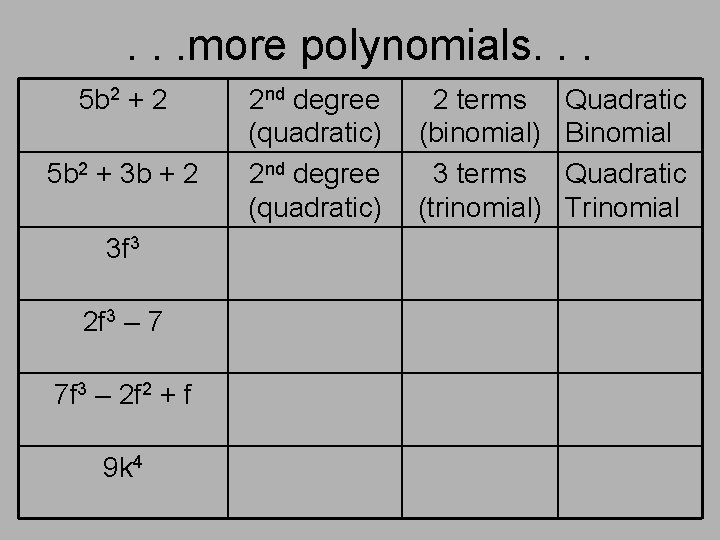
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 2 terms (binomial) 3 terms (trinomial) Quadratic Binomial Quadratic Trinomial

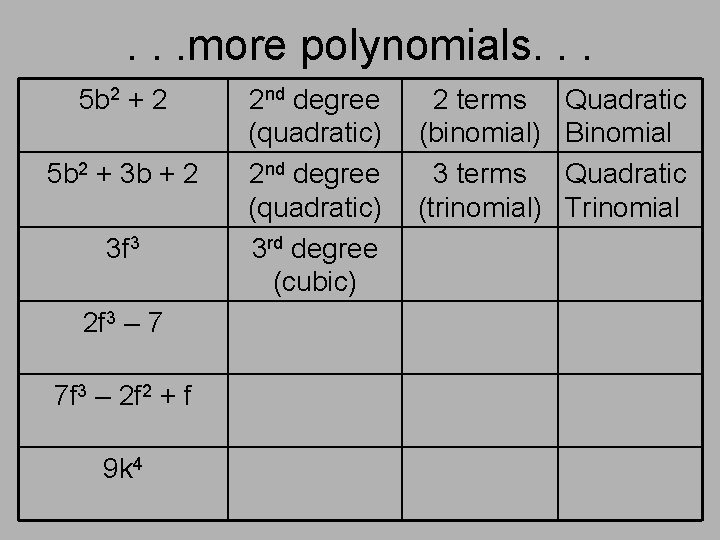
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 2 terms (binomial) 3 terms (trinomial) Quadratic Binomial Quadratic Trinomial

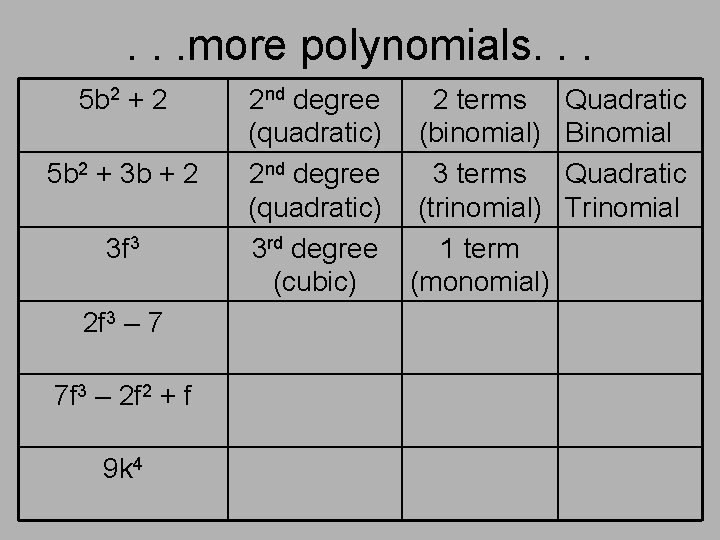
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) Quadratic Binomial Quadratic Trinomial

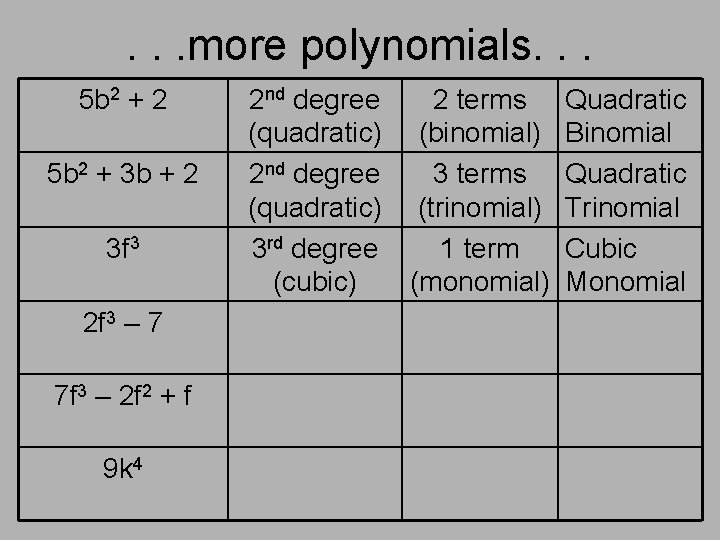
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) Quadratic Binomial Quadratic Trinomial Cubic Monomial

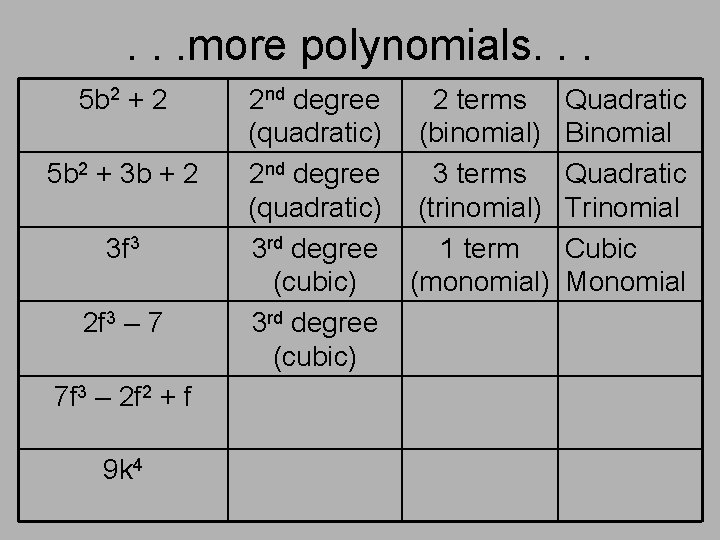
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) Quadratic Binomial Quadratic Trinomial Cubic Monomial

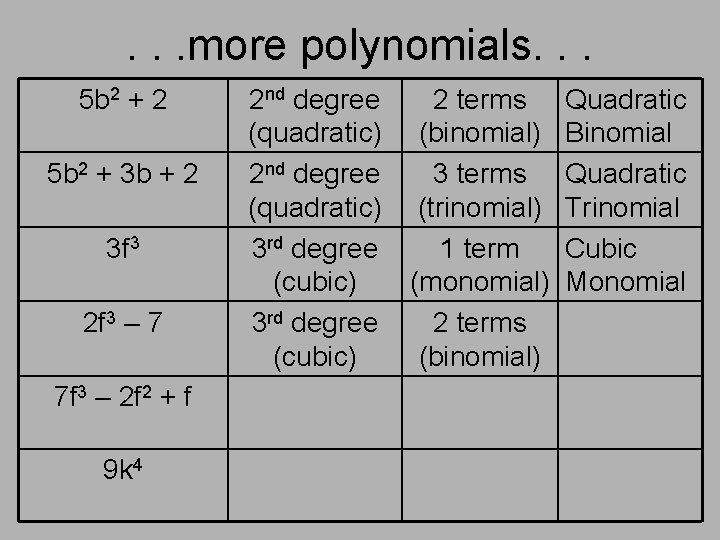
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) 2 terms (binomial) Quadratic Binomial Quadratic Trinomial Cubic Monomial

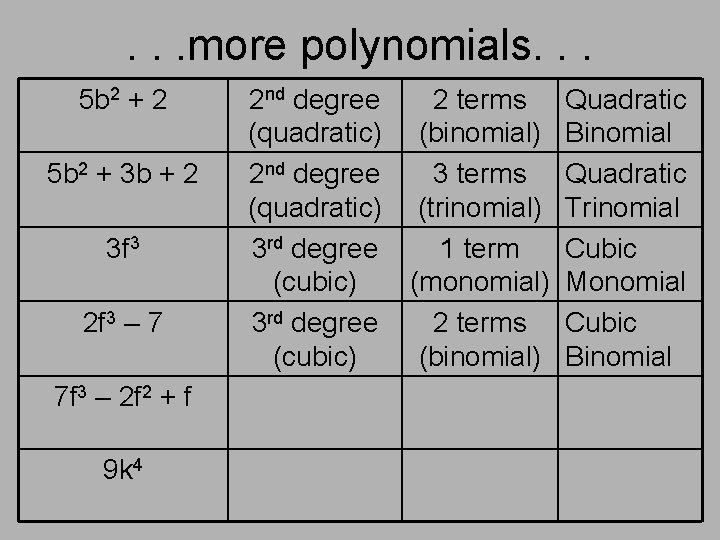
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) 2 terms (binomial) Quadratic Binomial Quadratic Trinomial Cubic Monomial Cubic Binomial

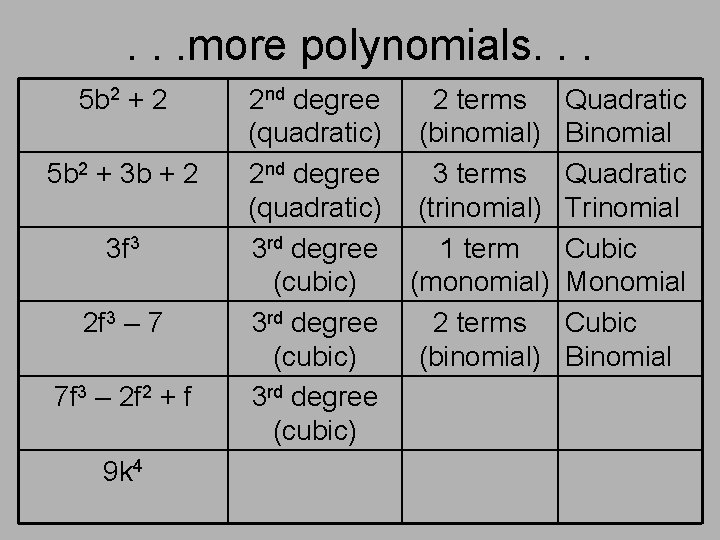
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) 2 terms (binomial) Quadratic Binomial Quadratic Trinomial Cubic Monomial Cubic Binomial

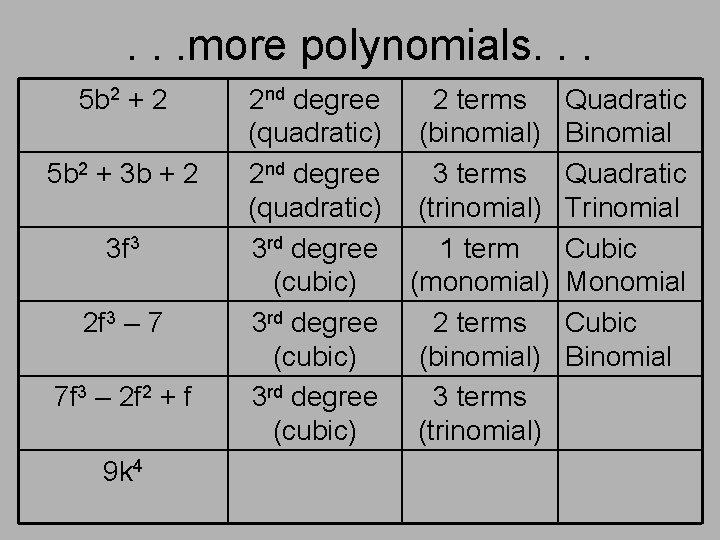
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) 2 terms (binomial) 3 terms (trinomial) Quadratic Binomial Quadratic Trinomial Cubic Monomial Cubic Binomial

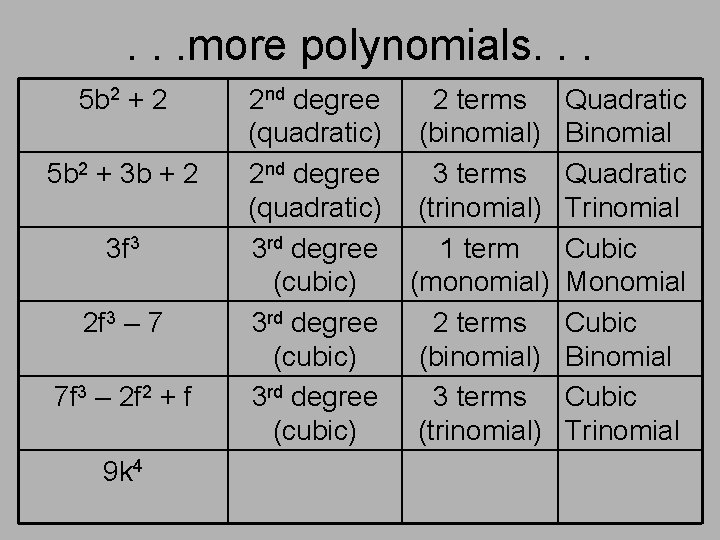
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) 2 terms (binomial) 3 terms (trinomial) Quadratic Binomial Quadratic Trinomial Cubic Monomial Cubic Binomial Cubic Trinomial

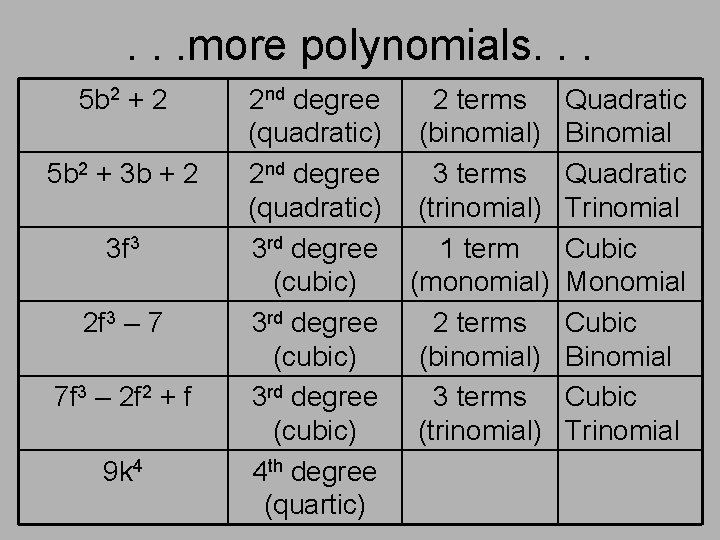
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 4 th degree (quartic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) 2 terms (binomial) 3 terms (trinomial) Quadratic Binomial Quadratic Trinomial Cubic Monomial Cubic Binomial Cubic Trinomial

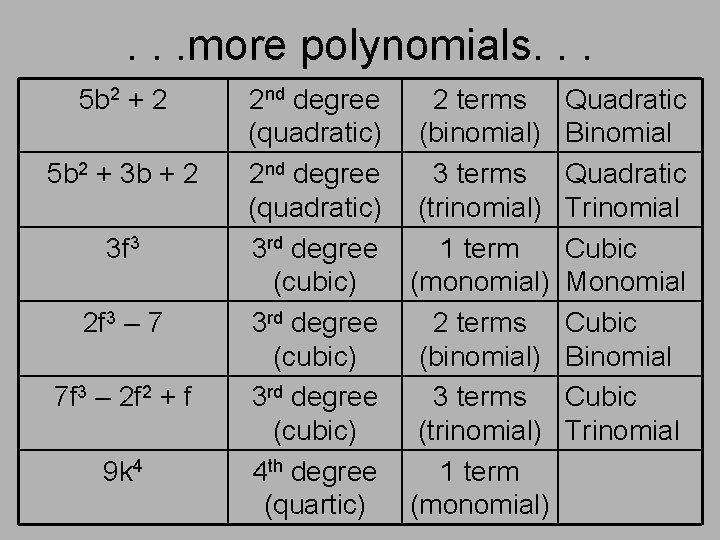
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 4 th degree (quartic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) Quadratic Binomial Quadratic Trinomial Cubic Monomial Cubic Binomial Cubic Trinomial

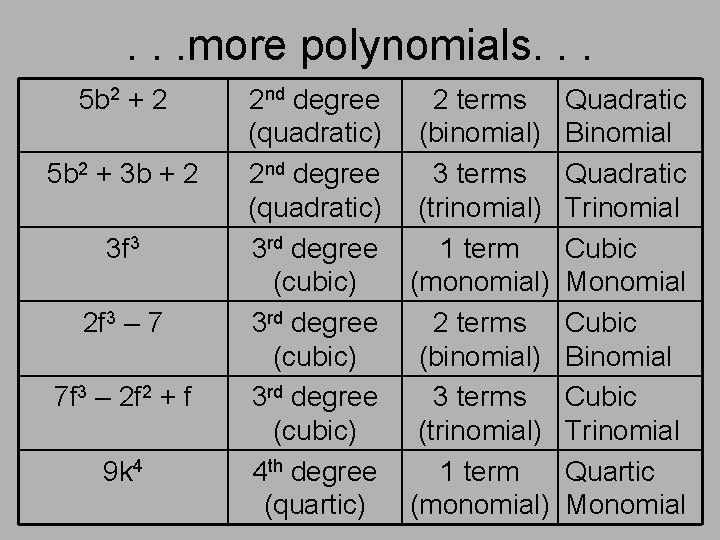
. . . more polynomials. . . 5 b 2 + 2 5 b 2 + 3 b + 2 3 f 3 2 f 3 – 7 7 f 3 – 2 f 2 + f 9 k 4 2 nd degree (quadratic) 3 rd degree (cubic) 4 th degree (quartic) 2 terms (binomial) 3 terms (trinomial) 1 term (monomial) Quadratic Binomial Quadratic Trinomial Cubic Monomial Cubic Binomial Cubic Trinomial Quartic Monomial

. . . more polynomials. . . 9 k 4 – 3 k 2 9 k 4 + 3 k 2 + 2 v 5 – 7 v f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8

. . . more polynomials. . . 9 k 4 – 3 k 2 9 k 4 + 3 k 2 + 2 v 5 – 7 v f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8 4 th degree (quartic)

. . . more polynomials. . . 9 k 4 – 3 k 2 9 k 4 + 3 k 2 + 2 v 5 – 7 v f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8 4 th degree (quartic) 2 terms (binomial)

. . . more polynomials. . . 9 k 4 – 3 k 2 9 k 4 + 3 k 2 + 2 v 5 – 7 v f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8 4 th degree (quartic) 2 terms (binomial) Quartic Binomial

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 9 k 4 + 3 k 2 + 2 4 th degree (quartic) v 5 – 7 v f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8 2 terms (binomial) Quartic Binomial

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) v 5 – 7 v f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8 Quartic Binomial

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 – 7 v f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) v 5 – 7 v f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term (monomial) v 5 – 7 v f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term Quintic (monomial) Monomial v 5 – 7 v f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term Quintic (monomial) Monomial v 5 – 7 v 5 th degree (quintic) f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term Quintic (monomial) Monomial v 5 – 7 v 5 th degree (quintic) f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8 2 terms (binomial)

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term Quintic (monomial) Monomial v 5 – 7 v 5 th degree (quintic) f 5 – 2 f 4 + f 2 j 7 - 2 j 5 + 7 j 3 - 8 2 terms (binomial) Quintic Binomial

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term Quintic (monomial) Monomial v 5 – 7 v 5 th degree (quintic) f 5 – 2 f 4 + f 2 5 th degree (quintic) j 7 - 2 j 5 + 7 j 3 - 8 2 terms (binomial) Quintic Binomial

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term Quintic (monomial) Monomial v 5 – 7 v 5 th degree (quintic) 2 terms (binomial) f 5 – 2 f 4 + f 2 5 th degree (quintic) 3 terms (trinomial) j 7 - 2 j 5 + 7 j 3 - 8 Quintic Binomial

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term Quintic (monomial) Monomial v 5 – 7 v 5 th degree (quintic) 2 terms (binomial) Quintic Binomial f 5 – 2 f 4 + f 2 5 th degree (quintic) 3 terms (trinomial) Quintic Trinomial j 7 - 2 j 5 + 7 j 3 - 8

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term Quintic (monomial) Monomial v 5 – 7 v 5 th degree (quintic) 2 terms (binomial) Quintic Binomial f 5 – 2 f 4 + f 2 5 th degree (quintic) 3 terms (trinomial) Quintic Trinomial j 7 - 2 j 5 + 7 j 3 - 8 7 th degree (7 th degree)

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term Quintic (monomial) Monomial v 5 – 7 v 5 th degree (quintic) 2 terms (binomial) Quintic Binomial f 5 – 2 f 4 + f 2 5 th degree (quintic) 3 terms (trinomial) Quintic Trinomial j 7 - 2 j 5 + 7 j 3 - 8 7 th degree (7 th degree) 4 terms (polynomial with 4 terms)

. . . more polynomials. . . 9 k 4 – 3 k 2 4 th degree (quartic) 2 terms (binomial) Quartic Binomial 9 k 4 + 3 k 2 + 2 4 th degree (quartic) 3 terms (trinomial) Quartic Trinomial v 5 5 th degree (quintic) 1 term Quintic (monomial) Monomial v 5 – 7 v 5 th degree (quintic) 2 terms (binomial) Quintic Binomial f 5 – 2 f 4 + f 2 5 th degree (quintic) 3 terms (trinomial) Quintic Trinomial j 7 - 2 j 5 + 7 j 3 - 8 7 th degree (7 th degree) 4 terms 7 th degree polynomial with 4 terms (polynomial with 4 terms)

Can you name them now? Give it a try. . . copy and classify (2 columns): 1. 2. 3. 4. 5. POLYNOMIAL 5 x 2 – 2 x + 3 2 z + 5 7 a 3 + 4 a – 12 -15 27 x 8 + 3 x 5 – 7 x + 4 6. 9 x 4 – 3 7. 10 x – 185 8. 18 x 5 CLASSIFICATION / NAME 1. Quadratic Trinomial 2. Linear Binomial 3. Cubic Trinomial 4. Constant Monomial 5. 8 th Degree Polynomial with 4 terms. 6. Quartic Binomial 7. Linear Binomial 8. Quintic Monomial

. . . more practice. . . 9. 19 z 25 10. 6 n 7 + 3 n 5 – 4 n 11. 189 12. 15 g 5 + 3 g 4 – 3 g – 7 13. 3 x 9 + 12 14. 6 z 3 – 2 z 2 + 4 z + 7 15. 9 c 16. 15 b 2 – b + 51 9. 25 th degree Monomial 10. 7 th degree Trinomial 11. Constant Monomial 12. Quintic polynomial with 4 terms 13. 9 th degree Binomial 14. Cubic polynomial with 4 terms. 15. Linear Monomial 16. Quadratic Trinomial

Create-A-Polynomial Activity: • You will need one sheet of paper, a pencil, and your notes on Classifying Polynomials. • You will be given the names of some polynomials. YOU must create a correct matching example, but REMEMBER: – Answers must be in standard form. – Each problem can only use one variable throughout the problem (see examples in notes from powerpoint). – All variable powers in each example must have DIFFERENT exponents (again, see examples in notes from powerpoint). – There can only be one constant in each problem. • You will need two columns on your paper. – Left column title: Polynomial Name – Right column title: Polynomial in Standard Form.

Create - A – Polynomial Activity: Copy each polynomial name. Create your own polynomial to match ( 2 columns). Partner/Independent work (pairs). 1. 6 th degree polynomial with 4 terms. 2. Linear Monomial 3. Quadratic Trinomial 4. Constant Monomial 5. Cubic Binomial 6. Quartic Monomial 7. Quintic polynomial with 5 terms. 8. Linear Binomial 9. Cubic Trinomial 10. Quadratic Binomial 11. Quintic Trinomial 12. Constant Monomial 13. Cubic Monomial 14. 10 th degree polynomial with 6 terms 15. 8 th degree Binomial 16. 20 th degree Trinomial