Classifying Polynomials Degree of a Polynomial The degree

Classifying Polynomials

Degree of a Polynomial The degree of a polynomial is calculated by finding the largest exponent in the polynomial.

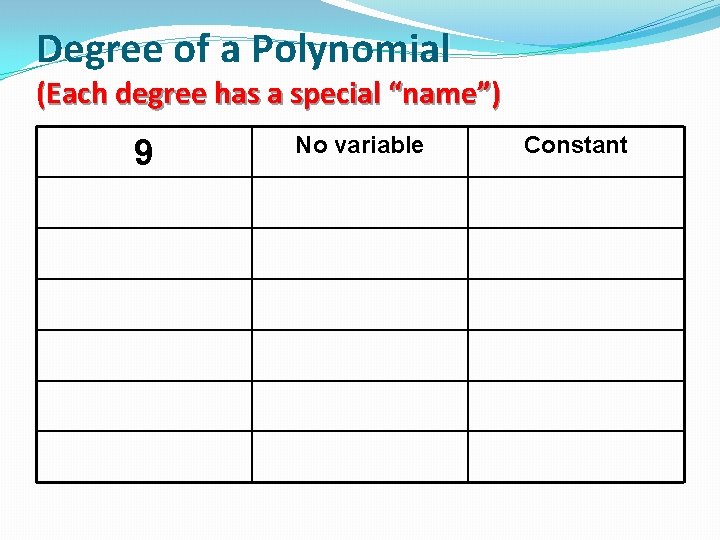
Degree of a Polynomial (Each degree has a special “name”) 9

Degree of a Polynomial (Each degree has a special “name”) 9 No variable Constant

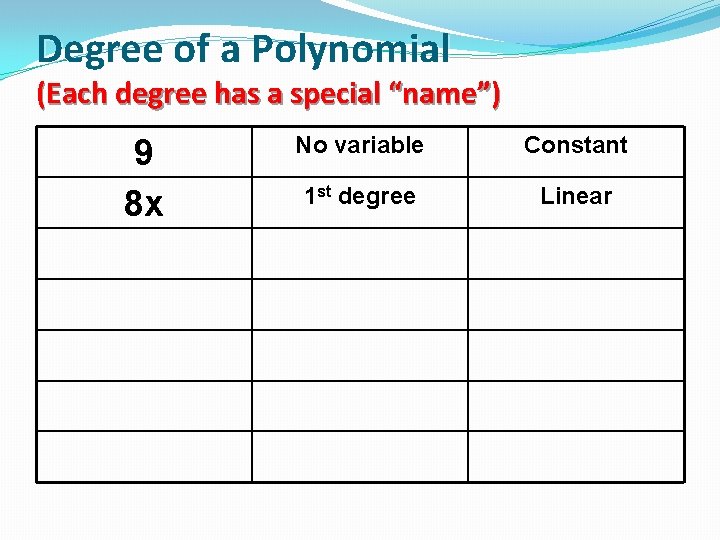
Degree of a Polynomial (Each degree has a special “name”) 9 8 x No variable Constant 1 st degree Linear

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x No variable Constant 1 st degree Linear 2 nd degree Quadratic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic 4 th degree Quartic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 2 x 5 + 7 x 3 No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic 4 th degree Quartic 5 th degree Quintic

Degree of a Polynomial (Each degree has a special “name”) 9 8 x 7 x 2 + 3 x 6 x 3 – 2 x 3 x 4 + 5 x – 1 2 x 5 + 7 x 3 5 xn No variable Constant 1 st degree Linear 2 nd degree Quadratic 3 rd degree Cubic 4 th degree Quartic 5 th degree Quintic 6 th degree or higher “nth” degree

Let’s practice classifying polynomials by “degree”. 1. 2. 3. 4. 5. 6. 7. 8. 9. POLYNOMIAL 3 z 4 + 5 z 3 – 7 15 a + 25 185 2 c 10 – 7 c 6 + 4 c 3 - 9 2 f 3 – 7 f 2 + 1 15 y 2 9 g 4 – 3 g + 5 10 r 5 – 7 r 16 n 7 + 6 n 4 – 3 n 2 1. 2. 3. 4. 5. 6. 7. 8. 9. DEGREE NAME Quartic Linear Constant Tenth degree Cubic Quadratic Quartic Quintic Seventh degree The degree name becomes the “first name” of the polynomial.

Naming Polynomials (by number of terms)

Naming Polynomials (by number of terms) One term Monomial

Naming Polynomials (by number of terms) One term Monomial Two terms Binomial

Naming Polynomials (by number of terms) One term Monomial Two terms Binomial Three terms Trinomial

Naming Polynomials (by number of terms) One term Monomial Two terms Binomial Three terms Trinomial Four (or more) Polynomial with 4 (or more) terms

Let’s practice classifying a polynomial by “number of terms”. Polynomial 1. 2. 3. 4. 5. 6. 7. 8. 15 x 2 e 8 – 3 e 7 + 3 e – 7 6 c + 5 3 y 7 – 4 y 5 + 8 y 3 64 2 p 8 – 4 p 6 + 9 p 4 + 3 p – 1 25 h 3 – 15 h 2 + 18 55 c 19 + 35 1. 2. 3. 4. 5. 6. 7. 8. Classify by # of Terms: Monomial Polynomial with 4 terms Binomial Trinomial Monomial Polynomial with 5 terms Trinomial Binomial

Can you name them now? 1. 2. 3. 4. 5. POLYNOMIAL 5 x 2 – 2 x + 3 2 z + 5 7 a 3 + 4 a – 12 -15 27 x 8 + 3 x 5 – 7 x + 4 6. 9 x 4 – 3 7. 10 x – 185 8. 18 x 5 CLASSIFICATION / NAME 1. Quadratic Trinomial 2. Linear Binomial 3. Cubic Trinomial 4. Constant Monomial 5. 8 th Degree Polynomial with 4 terms. 6. Quartic Binomial 7. Linear Binomial 8. Quintic Monomial