Classifying Numbers Whole Numbers Integers Rational Numbers Irrational

Classifying Numbers Whole Numbers Integers Rational Numbers Irrational Numbers Real Numbers

Warm-up 10 August 2017 •

Whole numbers consist of any positive number which does not have fractional parts. This set also includes zero. 0, 1, 2, 3, 4, 5, 6, 7, … Fractions Mixed Numbers Negative Numbers

Integers are whole numbers both positive and negative. This set also includes zero. …, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … Fractions Mixed Numbers

Notice that the set of whole numbers is included in the set of integers. Integers Whole Numbers

Rational numbers include all integers as well as terminating & repeating decimals, fractions, and mixed number. …, -3, -2. 75, -2, -1, 0, ½, . 7, 1, 2, 3, 3. 5 … Nonterminating, nonrepeating decimals

What isn’t a rational number

These numbers are irrational. They are nonrepeating, nonterminating decimals. = 3. 141592653… Note: These are square roots of non-perfect squares. = 1. 414213562… = 2. 23606797…

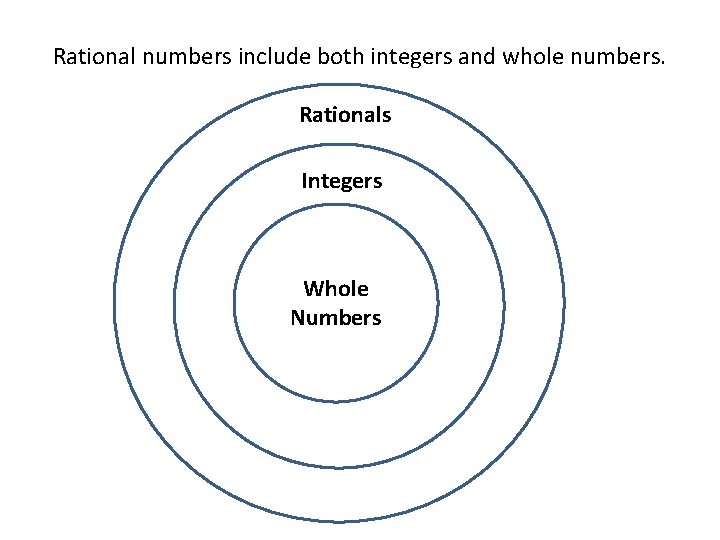
Rational numbers include both integers and whole numbers. Rationals Integers Whole Numbers

Classify each number as whole, integer, or rational. You may give multiple names to each number. 1) . 7 2) -4 3) 2. 75 4) . 3 5) 25 6) -2½

Classify each number as whole, integer, or rational. You may give multiple names to each number. 1) . 7 2) -4 3) 2. 75 4) . 3 5) 25 6) -2½ rational

Classify each number as whole, integer, or rational. You may give multiple names to each number. 1) . 7 rational 2) -4 integer, rational 3) 2. 75 4) . 3 5) 25 6) -2½

Classify each number as whole, integer, or rational. You may give multiple names to each number. 1) . 7 rational 2) -4 integer, rational 3) 2. 75 rational 4) . 3 5) 25 6) -2½

Classify each number as whole, integer, or rational. You may give multiple names to each number. 1) . 7 rational 2) -4 integer, rational 3) 2. 75 rational 4) . 3 5) 25 6) -2½ rational

Classify each number as whole, integer, or rational. You may give multiple names to each number. 1) . 7 rational 2) -4 integer, rational 3) 2. 75 rational 4) . 3 rational 5) 25 whole, integer, rational 6) -2½

Classify each number as whole, integer, or rational. You may give multiple names to each number. 1) 0. 7 rational 2) -4 integer, rational 3) 2. 75 rational 4) 0. 3 rational 5) 25 whole, integer, rational 6) -2½ rational

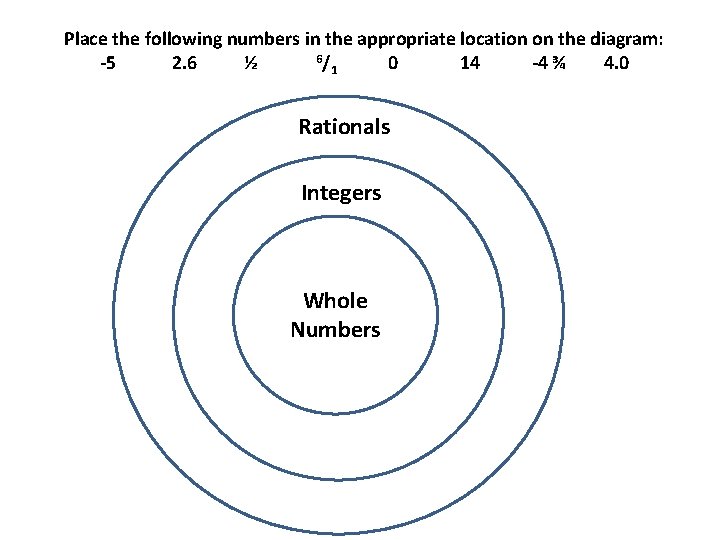
Place the following numbers in the appropriate location on the diagram: 6/ -5 2. 6 ½ 0 14 -4 ¾ 4. 0 1 Rationals Integers Whole Numbers

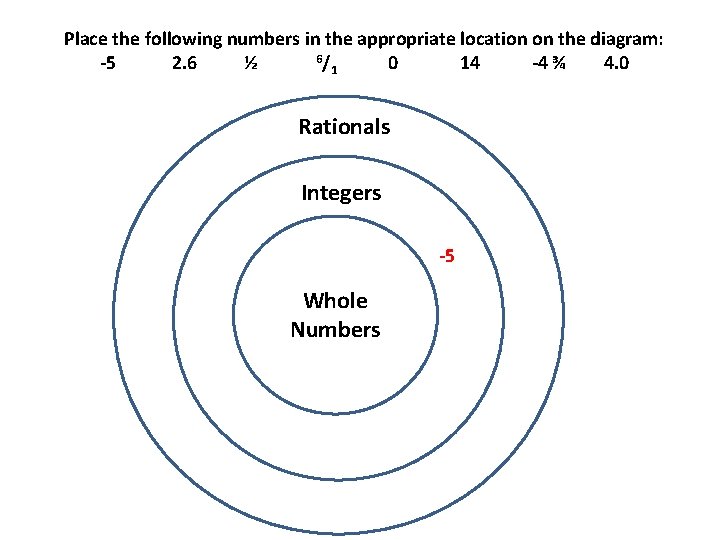
Place the following numbers in the appropriate location on the diagram: 6/ -5 2. 6 ½ 0 14 -4 ¾ 4. 0 1 Rationals Integers -5 Whole Numbers

Place the following numbers in the appropriate location on the diagram: 6/ -5 2. 6 ½ 0 14 -4 ¾ 4. 0 1 Rationals 2. 6 Integers -5 Whole Numbers

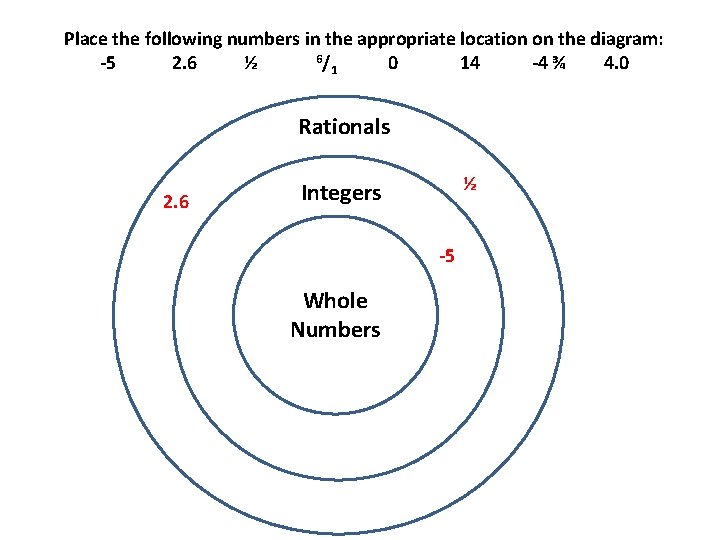
Place the following numbers in the appropriate location on the diagram: 6/ -5 2. 6 ½ 0 14 -4 ¾ 4. 0 1 Rationals 2. 6 ½ Integers -5 Whole Numbers

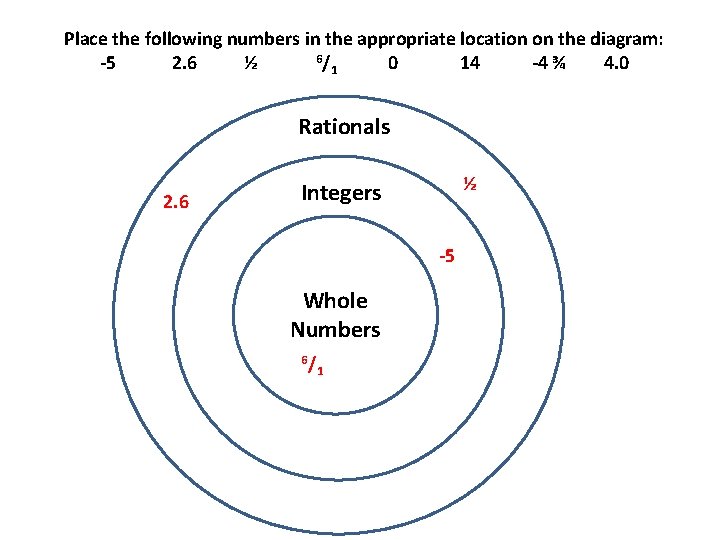
Place the following numbers in the appropriate location on the diagram: 6/ -5 2. 6 ½ 0 14 -4 ¾ 4. 0 1 Rationals 2. 6 ½ Integers -5 Whole Numbers 6/ 1

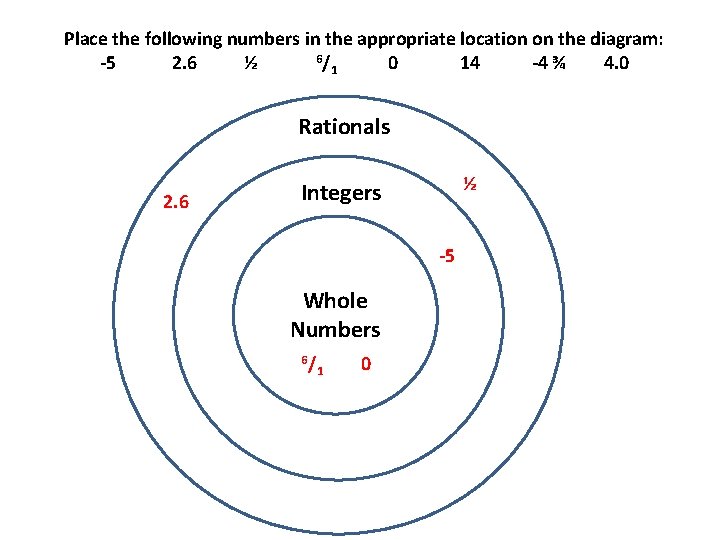
Place the following numbers in the appropriate location on the diagram: 6/ -5 2. 6 ½ 0 14 -4 ¾ 4. 0 1 Rationals 2. 6 ½ Integers -5 Whole Numbers 6/ 1 0

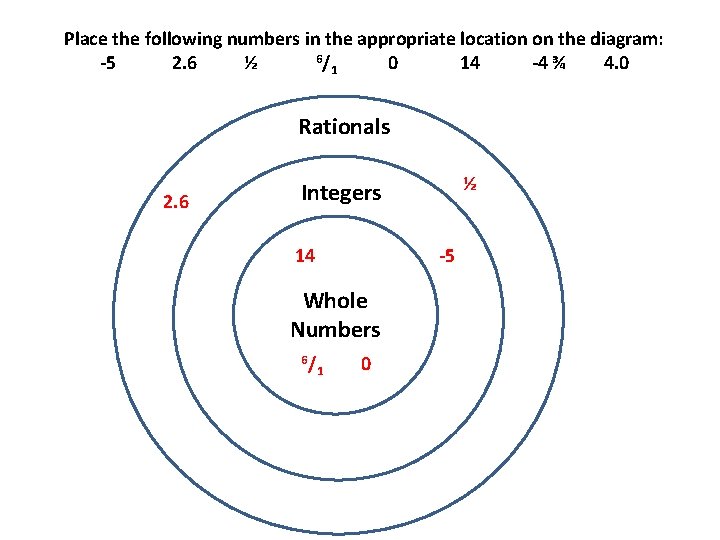
Place the following numbers in the appropriate location on the diagram: 6/ -5 2. 6 ½ 0 14 -4 ¾ 4. 0 1 Rationals 2. 6 ½ Integers 14 -5 Whole Numbers 6/ 1 0

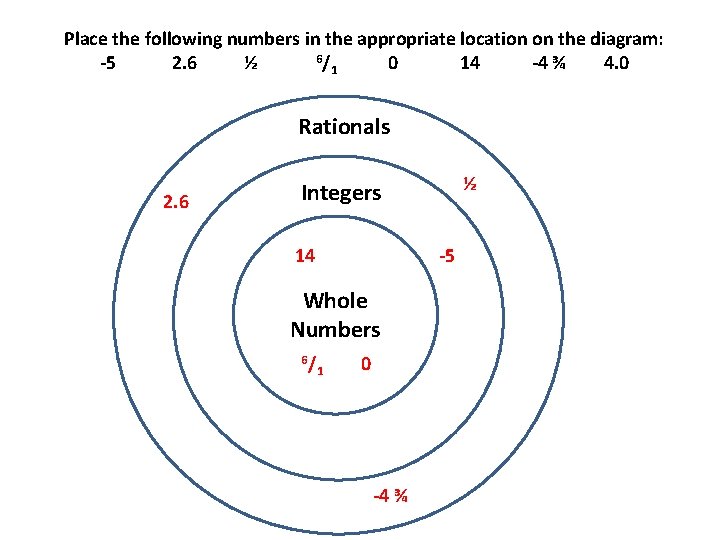
Place the following numbers in the appropriate location on the diagram: 6/ -5 2. 6 ½ 0 14 -4 ¾ 4. 0 1 Rationals 2. 6 ½ Integers 14 -5 Whole Numbers 6/ 1 0 -4 ¾

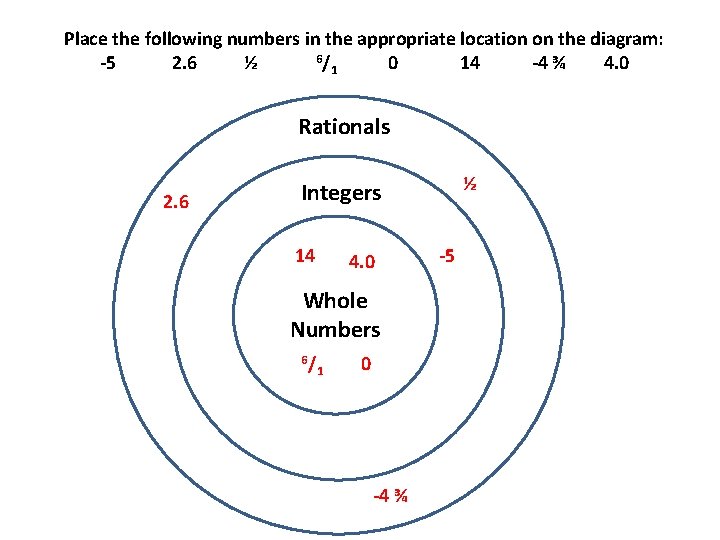
Place the following numbers in the appropriate location on the diagram: 6/ -5 2. 6 ½ 0 14 -4 ¾ 4. 0 1 Rationals 2. 6 ½ Integers 14 4. 0 Whole Numbers 6/ 1 0 -4 ¾ -5

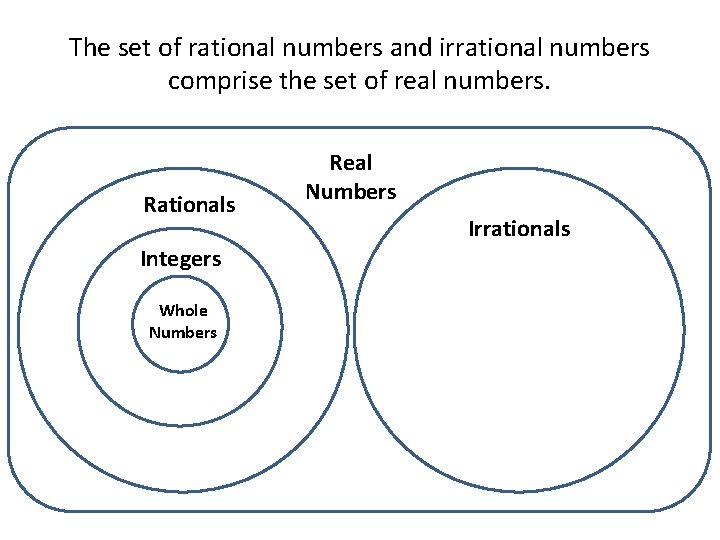
The set of rational numbers and irrational numbers comprise the set of real numbers. Rationals Integers Whole Numbers Real Numbers Irrationals

Decide whether each number is rational or irrational. 1) 2) 3) -6 4) 5) 2. 454545… 6) 7. 25 7) 8)

Decide whether each number is rational or irrational. 1) rational 2) 3) -6 4) 5) 2. 454545… 6) 7. 25 7) 8)

Decide whether each number is rational or irrational. 1) rational 2) irrational 3) -6 4) 5) 2. 454545… 6) 7. 25 7) 8)

Decide whether each number is rational or irrational. 1) rational 2) irrational 3) -6 rational 4) 5) 2. 454545… 6) 7. 25 7) 8)

Decide whether each number is rational or irrational. 1) rational 2) irrational 3) -6 4) rational 5) 2. 454545… 6) 7. 25 7) 8)

Decide whether each number is rational or irrational. 1) rational 2) irrational 3) -6 4) rational 5) 2. 454545… irrational 6) 7. 25 7) 8)

Decide whether each number is rational or irrational. 1) rational 2) irrational 3) 4) -6 rational 5) 2. 454545… irrational 6) 7. 25 rational 7) 8)

Decide whether each number is rational or irrational. 1) rational 2) irrational 3) 4) -6 rational 5) 2. 454545… irrational 6) 7. 25 rational 7) 8) irrational

Decide whether each number is rational or irrational. 1) rational 2) irrational 3) 4) -6 rational 5) 2. 454545… irrational 6) 7. 25 rational 7) irrational 8) irrational

What isn’t a real number

These “numbers” are NOT real numbers. You cannot find the square root of a negative number. You cannot divide by zero.

Classify each number as real or not real. 1) 2) 3) 4) 5)

Classify each number as real or not real. 1) 2) 3) 4) 5) Not real

Classify each number as real or not real. 1) Not real 2) Real 3) 4) 5)

Classify each number as real or not real. 1) Not real 2) Real 3) Real 4) 5)

Classify each number as real or not real. 1) Not real 2) Real 3) Real 4) Not real 5)

Classify each number as real or not real. 1) Not real 2) Real 3) Real 4) Not real 5) Not real

Whole Numbers 0 1 2 3

Integers -3 -2 -1 0 1 2 3

Rational Numbers -3 -2 -1 -. 75 0 1 2 3

Irrational Numbers π

REAL NUMBERS = Rational Numbers -3 -2 -1 -. 75 0 1 + Irrational Numbers π 2 3

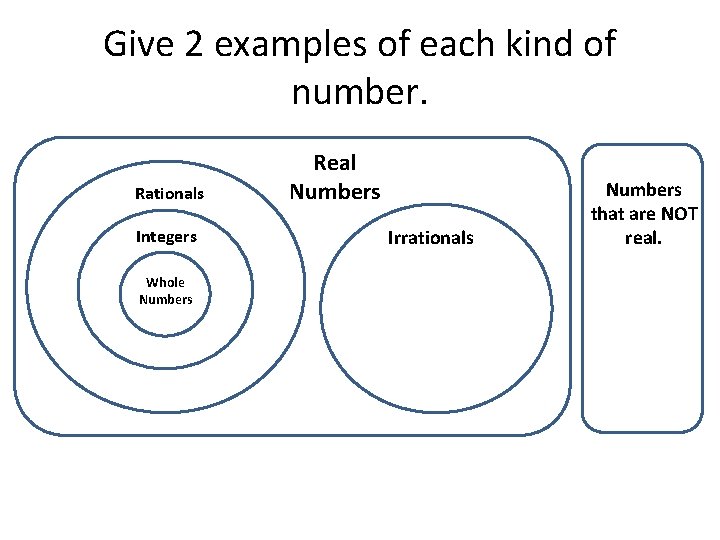
Give 2 examples of each kind of number. Rationals Integers Whole Numbers Real Numbers Irrationals Numbers that are NOT real.