Classifying Beamsplitters Adam Bouland BosonFermion Model M modes

Classifying Beamsplitters Adam Bouland

Boson/Fermion Model M modes

Boson/Fermion Model
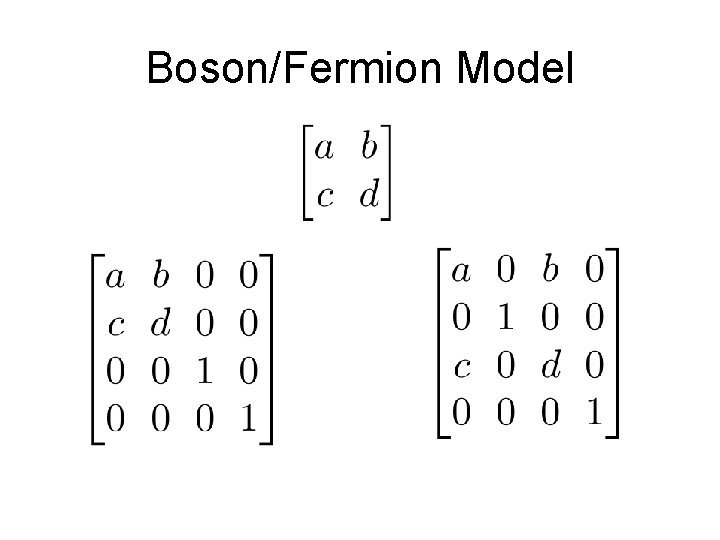
Boson/Fermion Model

Beamsplitters • Def: A set of beamsplitters is universal if it densely generates SU(m) or SO(m) on m modes.

Beamsplitters • Def: A set of beamsplitters is universal if it densely generates SU(m) or SO(m) on m modes. Q: Which sets of beamsplitters are universal?

Beamsplitters • Obviously not universal:

Beamsplitters • Obviously not universal: • Not obvious:
![Real Beamsplitters Thm: [B. Aaronson ’ 12] Any real nontrivial beamsplitter modes. is universal Real Beamsplitters Thm: [B. Aaronson ’ 12] Any real nontrivial beamsplitter modes. is universal](http://slidetodoc.com/presentation_image_h2/a188ade9dbcd64669f0e3169cafe3d93/image-9.jpg)
Real Beamsplitters Thm: [B. Aaronson ’ 12] Any real nontrivial beamsplitter modes. is universal on ≥ 3
![Real Beamsplitters Thm: [B. Aaronson ’ 12] Any real nontrivial beamsplitter is universal on Real Beamsplitters Thm: [B. Aaronson ’ 12] Any real nontrivial beamsplitter is universal on](http://slidetodoc.com/presentation_image_h2/a188ade9dbcd64669f0e3169cafe3d93/image-10.jpg)
Real Beamsplitters Thm: [B. Aaronson ’ 12] Any real nontrivial beamsplitter is universal on ≥ 3 modes. What about complex beamsplitters?

Complex Beamsplitters Goal: Any non-trivial (complex) beamsplitter is universal on ≥ 3 modes.

Complex Beamsplitters Goal: Any non-trivial (complex) beamsplitter is universal on ≥ 3 modes. Can show: Any non-trivial beamsplitter generates a continuous group on ≥ 3 modes.

Complex Beamsplitters Determinant ± 1

Complex Beamsplitters

Complex Beamsplitters Let G=<R 1, R 2, R 3>

Complex Beamsplitters

Complex Beamsplitters Subgroups of SU(3): 6 infinite families 12 exceptional groups

Complex Beamsplitters Subgroups of SU(3): 6 infinite families 12 exceptional groups

Complex Beamsplitters Let G=<R 1, R 2, R 3> Lemma: If G is discrete, R 1, R 2, R 3 form an irreducible representation of G.

Complex Beamsplitters

Complex Beamsplitters

Complex Beamsplitters Δ(6 n 2)

Complex Beamsplitters Δ(6 n 2) Algebraic Number Theory

Open questions • Can we complete the proof to show any beamsplitter is universal? • Can we extend this to multi-mode beamsplitters? • What if the beamsplitter applies a phase as well?

Questions ?
- Slides: 25