Classification Today Basic Problem Decision Trees Classification Problem

Classification Today: Basic Problem Decision Trees

Classification Problem • Given a database D={t 1, t 2, …, tn} and a set of classes C={C 1, …, Cm}, the Classification Problem is to define a mapping f: Dg. C where each ti is assigned to one class. • Actually divides D into equivalence classes. • Prediction is similar, but may be viewed as having infinite number of classes.

Classification Ex: Grading x <90 >=90 • If x >= 90 then grade =A. • If 80<=x<90 then grade x A =B. <80 >=80 • If 70<=x<80 then grade x B =C. • If 60<=x<70 then grade <70 >=70 x =D. C • If x<50 then grade =F. <50 >=60 F D

Classification Techniques • Approach: 1. Create specific model by evaluating training data (or using domain experts’ knowledge). 2. Apply model developed to new data. • Classes must be predefined • Most common techniques use DTs, or are based on distances or statistical methods.

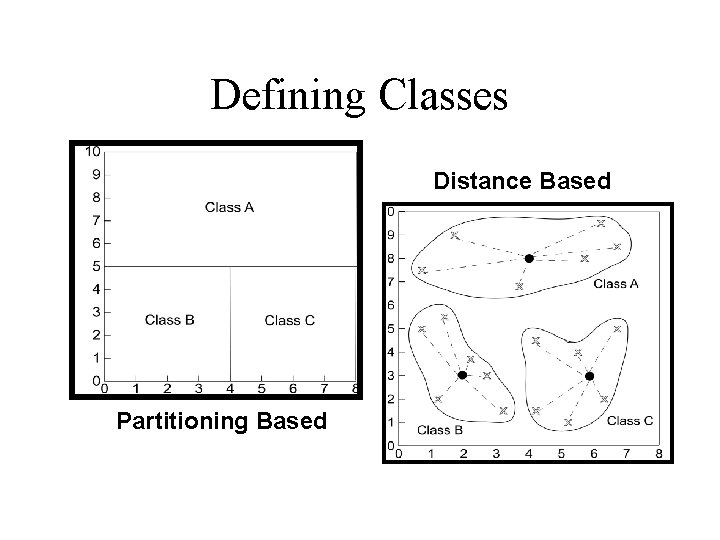
Defining Classes Distance Based Partitioning Based

Issues in Classification • Missing Data – Ignore – Replace with assumed value • Measuring Performance – Classification accuracy on test data – Confusion matrix – OC Curve

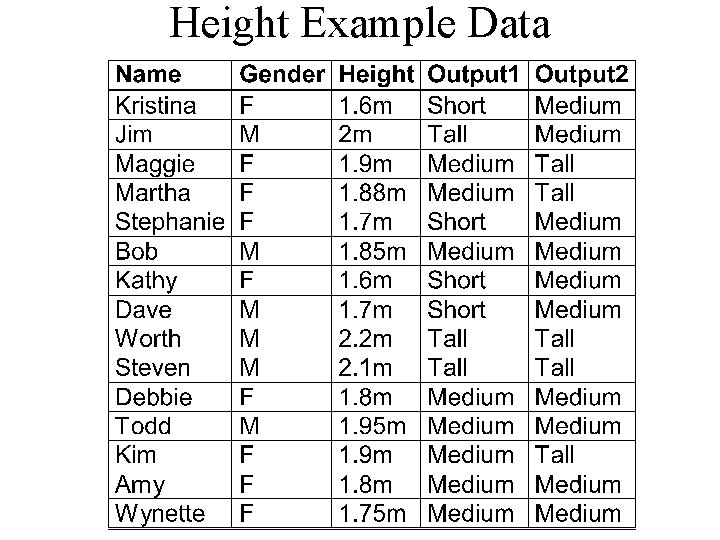
Height Example Data

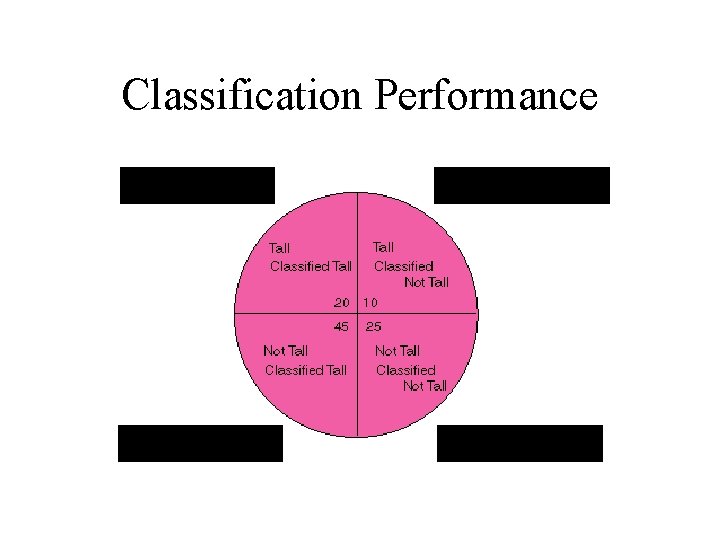
Classification Performance True Positive False Negative False Positive True Negative

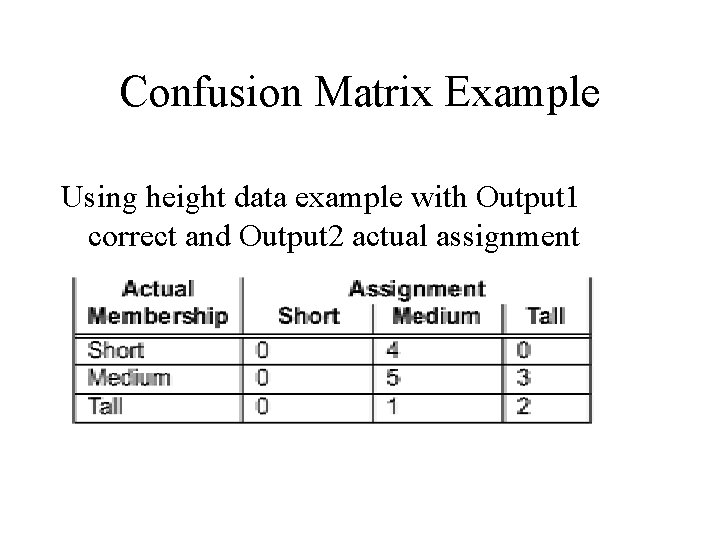
Confusion Matrix Example Using height data example with Output 1 correct and Output 2 actual assignment

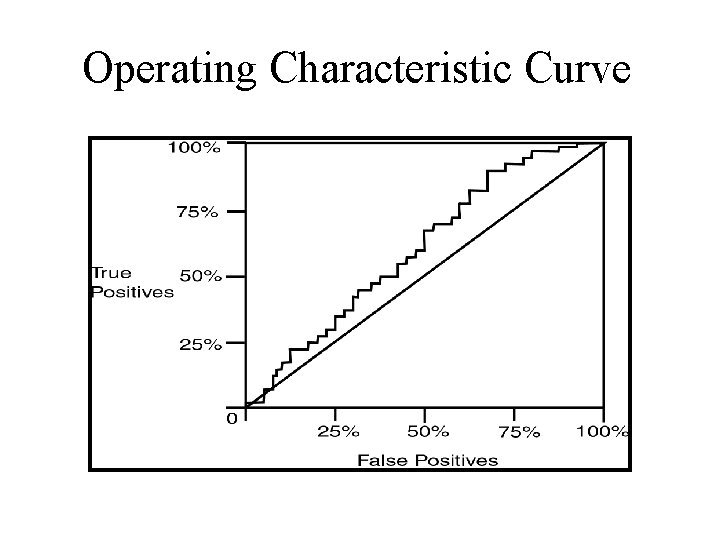
Operating Characteristic Curve

Classification Using Decision Trees • Partitioning based: Divide search space into rectangular regions. • Tuple placed into class based on the region within which it falls. • DT approaches differ in how the tree is built: DT Induction • Internal nodes associated with attribute and arcs with values for that attribute. • Algorithms: ID 3, C 4. 5, CART

Decision Tree Given: – D = {t 1, …, tn} where ti=<ti 1, …, tih> – Database schema contains {A 1, A 2, …, Ah} – Classes C={C 1, …. , Cm} Decision or Classification Tree is a tree associated with D such that – Each internal node is labeled with attribute, Ai – Each arc is labeled with predicate which can be applied to attribute at parent – Each leaf node is labeled with a class, Cj

DT Induction

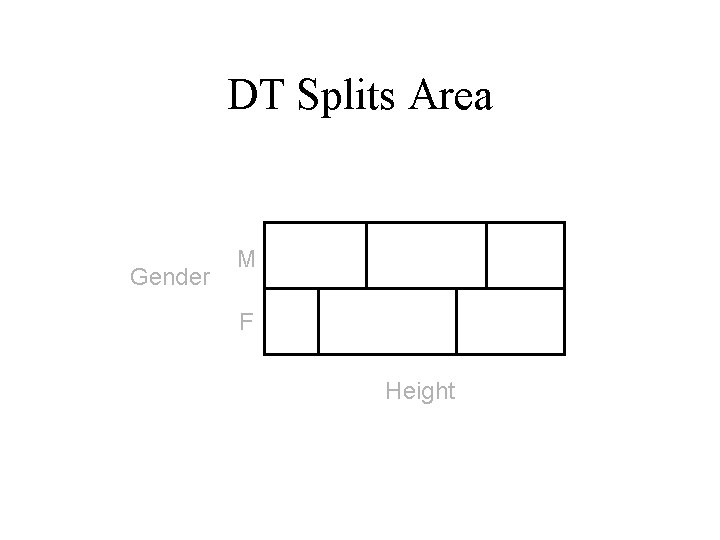
DT Splits Area Gender M F Height

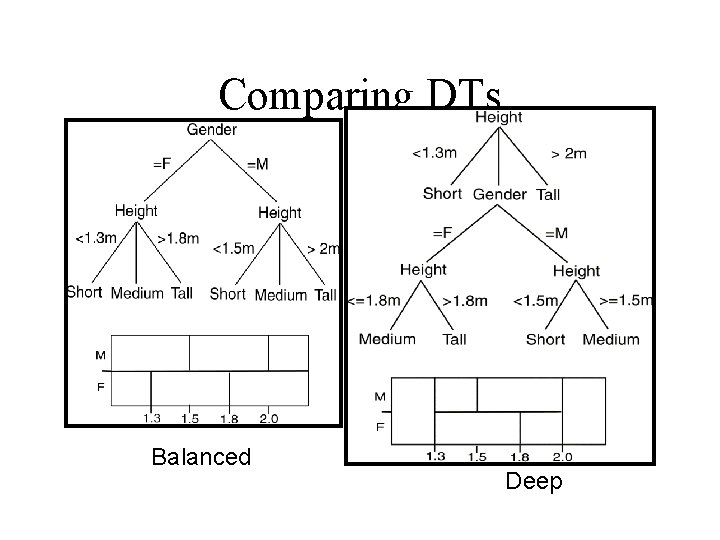
Comparing DTs Balanced Deep

DT Issues • • Choosing Splitting Attributes Ordering of Splitting Attributes Splits Tree Structure Stopping Criteria Training Data Pruning

Information/Entropy • Given probabilitites p 1, p 2, . . , ps whose sum is 1, Entropy is defined as: • Entropy measures the amount of randomness or surprise or uncertainty. • Goal in classification – no surprise – entropy = 0

ID 3 • Creates tree using information theory concepts and tries to reduce expected number of comparison. . • ID 3 chooses split attribute with the highest information gain:

ID 3 Example (Output 1) Starting state entropy: • 4/15 log(15/4) + 8/15 log(15/8) + 3/15 log(15/3) = 0. 4384 • Gain using gender: – Female: 3/9 log(9/3)+6/9 log(9/6)=0. 2764 – Male: 1/6 (log 6/1) + 2/6 log(6/2) + 3/6 log(6/3) = 0. 4392 – Weighted sum: (9/15)(0. 2764) + (6/15)(0. 4392) = 0. 34152 – Gain: 0. 4384 – 0. 34152 = 0. 09688 • Gain using height: 0. 4384 – (2/15)(0. 301) = 0. 3983 • Choose height as first splitting attribute

• C 4. 5 ID 3 favors attributes with large number of divisions • Improved version of ID 3: – Missing Data – Continuous Data – Pruning – Rules – Gain. Ratio:

CART • Create Binary Tree • Uses entropy • Formula to choose split point, s, for node t: • PL, PR probability that a tuple in the training set will be on the left or right side of the tree.

CART Example • At the start, there are six choices for split point (right branch on equality): – P(Gender)=2(6/15)(9/15)(2/15 + 4/15 + 3/15)=0. 224 – P(1. 6) = 0 – P(1. 7) = 2(2/15)(13/15)(0 + 8/15 + 3/15) = 0. 169 – P(1. 8) = 2(5/15)(10/15)(4/15 + 6/15 + 3/15) = 0. 385 – P(1. 9) = 2(9/15)(6/15)(4/15 + 2/15 + 3/15) = 0. 256 – P(2. 0) = 2(12/15)(3/15)(4/15 + 8/15 + 3/15) = 0. 32 • Split at 1. 8

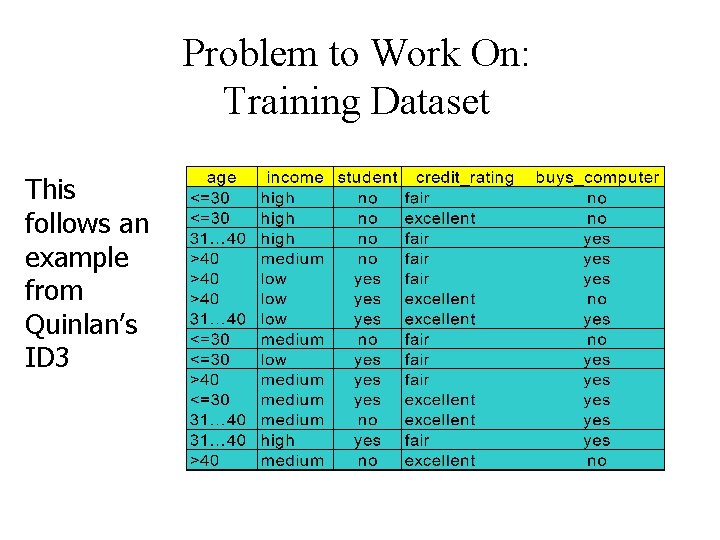
Problem to Work On: Training Dataset This follows an example from Quinlan’s ID 3

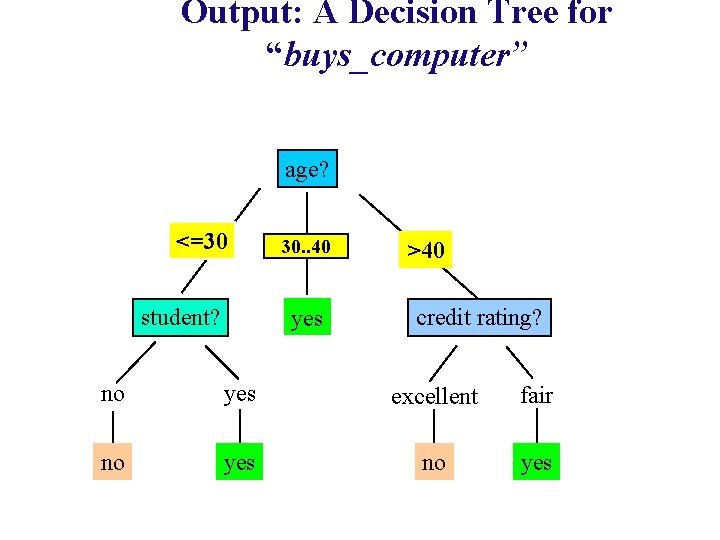
Output: A Decision Tree for “buys_computer” age? <=30 student? overcast 30. . 40 yes >40 credit rating? no yes excellent fair no yes

Bayesian Classification: Why? • Probabilistic learning: Calculate explicit probabilities for hypothesis, among the most practical approaches to certain types of learning problems • Incremental: Each training example can incrementally increase/decrease the probability that a hypothesis is correct. Prior knowledge can be combined with observed data. • Probabilistic prediction: Predict multiple hypotheses, weighted by their probabilities • Standard: Even when Bayesian methods are computationally intractable, they can provide a standard of optimal decision making against which other methods can be measured

Bayesian Theorem: Basics • Let X be a data sample whose class label is unknown • Let H be a hypothesis that X belongs to class C • For classification problems, determine P(H/X): the probability that the hypothesis holds given the observed data sample X • P(H): prior probability of hypothesis H (i. e. the initial probability before we observe any data, reflects the background knowledge) • P(X): probability that sample data is observed • P(X|H) : probability of observing the sample X, given that the hypothesis holds

Bayes Theorem (Recap) • Given training data X, posteriori probability of a hypothesis H, P(H|X) follows the Bayes theorem • MAP (maximum posteriori) hypothesis • Practical difficulty: require initial knowledge of many probabilities, significant computational cost; insufficient data

Naïve Bayes Classifier • A simplified assumption: attributes are conditionally independent: • The product of occurrence of say 2 elements x 1 and x 2, given the current class is C, is the product of the probabilities of each element taken separately, given the same class P([y 1, y 2], C) = P(y 1, C) * P(y 2, C) • No dependence relation between attributes • Greatly reduces the computation cost, only count the class distribution. • Once the probability P(X|Ci) is known, assign X to the class with maximum P(X|Ci)*P(Ci)

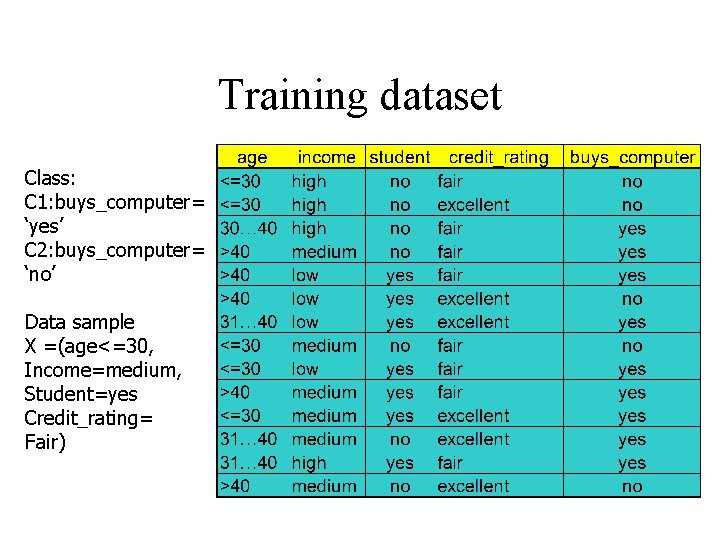
Training dataset Class: C 1: buys_computer= ‘yes’ C 2: buys_computer= ‘no’ Data sample X =(age<=30, Income=medium, Student=yes Credit_rating= Fair)

Naïve Bayesian Classifier: Example Compute P(X/Ci) for each class P(age=“<30” | buys_computer=“yes”) = 2/9=0. 222 P(age=“<30” | buys_computer=“no”) = 3/5 =0. 6 P(income=“medium” | buys_computer=“yes”)= 4/9 =0. 444 P(income=“medium” | buys_computer=“no”) = 2/5 = 0. 4 P(student=“yes” | buys_computer=“yes)= 6/9 =0. 667 P(student=“yes” | buys_computer=“no”)= 1/5=0. 2 P(credit_rating=“fair” | buys_computer=“yes”)=6/9=0. 667 P(credit_rating=“fair” | buys_computer=“no”)=2/5=0. 4 X=(age<=30 , income =medium, student=yes, credit_rating=fair) P(X|Ci) : P(X|buys_computer=“yes”)= 0. 222 x 0. 444 x 0. 667 x 0. 0. 667 =0. 044 P(X|buys_computer=“no”)= 0. 6 x 0. 4 x 0. 2 x 0. 4 =0. 019 Multiply by P(Ci)s and we can conclude that X belongs to class “buys_computer=yes”

Naïve Bayesian Classifier: Comments • Advantages : – Easy to implement – Good results obtained in most of the cases • Disadvantages – Assumption: class conditional independence , therefore loss of accuracy – Practically, dependencies exist among variables – E. g. , hospitals: patients: Profile: age, family history etc Symptoms: fever, cough etc. , Disease: lung cancer, diabetes etc – Dependencies among these cannot be modeled by Naïve Bayesian Classifier • How to deal with these dependencies? – Bayesian Belief Networks

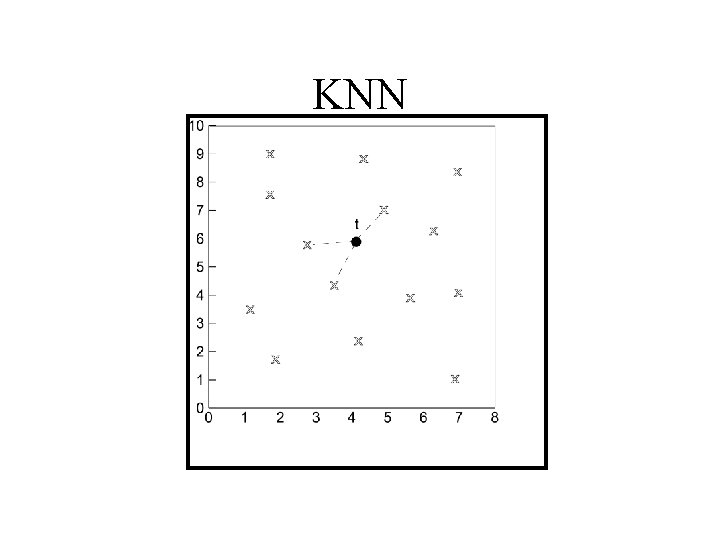
Classification Using Distance • Place items in class to which they are “closest”. • Must determine distance between an item and a class. • Classes represented by – Centroid: Central value. – Medoid: Representative point. – Individual points • Algorithm: KNN

K Nearest Neighbor (KNN): • Training set includes classes. • Examine K items near item to be classified. • New item placed in class with the most number of close items. • O(q) for each tuple to be classified. (Here q is the size of the training set. )

KNN

KNN Algorithm