Classification Theory and Universal Constructions in Categories of

Classification Theory and Universal Constructions in Categories of Musical Objects Guerino Mazzola U & ETH Zürich Internet Institute for Music Science guerino@mazzola. ch www. encyclospace. org

Contents • Enumeration of classical objects • Local classification techniques • Globalization and general addresses • Resolutions for global classification

Enumeration C Í Ÿ 12 (chords) M Í – 2 (motives) Enumeration = calculation of the number of orbits of a set C of such objects under the canonical left action G¥C ® C of a subgroup G Í Aff*(F) = e. F. GL(F) Ambient module F = Ÿ 12 , – 2 in the above examples

Enumeration 1973 A. Forte (1980 J. Rahn) List of 352 orbits of chords under the translation group T 12 = eŸ 12 and the group TI 12 = eŸ 12. ± 1 of translations and inversions on Ÿ 12 1978 G. Halsey/E. Hewitt • Recursive formula for enumeration of translation orbits of chords in finite abelian groups F • Enumeration of orbit numbers for chords in cyclic groups Ÿn, n c 24 1980 G. Mazzola • List of the 158 affine orbits of chords in Ÿ 12 • List of the 26 affine orbits of 3 -elt. motives in (Ÿ 12)2 and 45 in Ÿ 5 ¥ Ÿ 12 1989 H. Straub /E. Köhler List of the 216 affine orbits of 4 -element motives in (Ÿ 12)2 1991. . . H. Fripertinger • Enumeration formulas for Tn, TIn, and affine chord orbits in Ÿn, n-phonic k-series, all-interval series, and motives in Ÿn ¥ Ÿm 2 • Lists of affine motive orbits in (Ÿ 12) up to 6 elements, explicit formula. . .

Enumeration x^144 + x^143 + 5 x^142 + 26 x^141 + 216 x^140 + 2 024 x^139 + 27 806 x^138 + 417 209 x^137 +6 345 735 x^136 + 90 590 713 x^135 + 1 190 322 956 x^134 + 14 303 835 837 x^133 +157 430 569 051 x^132 + 1 592 645 620 686 x^131 + 14 873 235 105 552 x^130 + 128 762 751 824 308 x^129 + 1 037 532 923 086 353 x^128 + 7 809 413 514 931 644 x^127 +55 089 365 597 956 206 x^126 + 365 290 003 947 963 446 x^125 +2 282 919 558 918 081 919 x^124 + 13 479 601 808 118798 229 x^123 +75 361 590 622 423 713 249 x^122 + 399 738 890 367 674230 448 x^121 +2 015 334 387 723 540 077 262 x^120 + 9 673 558 570 858 327 142 094 x^119 + 44 275 002 111 552 677 715 575 x^118 + 193 497 799 414 541 699 555 587 x^117 +808 543 433 959 017 353 438 195 x^116 + 3 234 171 338 137 153 259 094292 x^115 +12 397 650 890 304 440 505 241198 x^114 + 45 591 347 244 850 943 472027 532 x^113 + 160 994 412 344 908 368 725 437 163 x^112 + 546 405 205 018 625 434 948486 100 x^111 +1 783 852 127 215 514 388 216 575 524 x^110 + 5 606 392 061 138 587 678 507 139 578 x^109 +16 974 908 597 922 176 404 758662 419 x^108 +49 548 380 452 249 950 392 015617 673 x^107 + 139 517 805 378 058 810 895 892 716 876 x^106 +379 202 235 047 824 659 955 968 634 895 x^105 +995 405 857 334 028 240 446 249 995 969 x^104 + 2 524 931 913 311 378 421 460 541 875 013 x^103 +6 192 094 899 403 308 142 319 324 646 830 x^102 + 14 688 225 057 065 816 000 841247 153 422 x^101 +33 716 152 882 551 682 431 054950 635 828 x^100 + 74 924 784 036 765 597 482 162224 697 378 x^99 +161 251 165 409 134 463 248 992 354 275 261 x^98 + 336 225 833 888 858 733 322 982 932 904 265 x^97 +679 456 372 086 288 422 448 712 466 252 503 x^96 + 1 331 179 830 182 151 403 666 404 596 530 852 x^95 +2 529 241 676 111 626 447 928 668 220 456 264 x^94 + 4 661 739 558 127 027 290 220 867 616 981 880 x^93 +8 337 341 899 567 786 249 391 103 289 453 916 x^92 + 14 472 367 067 576 451 752 984797 361 008 304 x^91 +24 388 618 572 337 747 341 932969 998 362 288 x^90 + 39 908 648 567 034 355 259 311114 115 744 392 x^89 +63 426 245 036 529 210 051 949169 850 308 102 x^88 + 97 921 220 397 909 924 969 018620 386 852 352 x^87 +146 881 830 585 458 073 270 850 321 720 445 928 x^86 + 214 098 939 483 879 341 610 433 150 629 060 274 x^85 +303 306 830 919 747 863 651 620 555 026 700 930 x^84 + 417 668 422 888 061 171 460 770 548 484 103 836 x^83 +559 136 759 653 084 522 330 064 385 877 590 780 x^82 + 727 765 306 194 069 123 565 702 210 626 823 392 x^81 +921 077 965 629 957 077 012 552 741 715 036 692 x^80 + 1 133 634 419 214 796 834 928 853 170 296 724314 x^79 +1 356 926 047 220 511 677 349 073 201 120 481570 x^78 + 1 579 704 950 475 555 411 914 967 237 903 930342 x^77 +1 788 783 546 844 376 088 722 000 995 922 467990 x^76 + 1 970 254 341 437 213 013 502 048 964 983 877090 x^75 +2 110 986 794 386 177 596 749 436 553 816 924660 x^74 + 2 200 183 419 494 435 885 449 671 402 432 366956 x^73 +2 230 741 522 540 743 033 415 296 821 609 381912 x^72 + …. … . . . + 2024. x 5 + 216. x 4 + 26. x 3 + 5. x 2 + x + 1 = cycle index polynomial 2 230 741 522 540 743 033 415 296 821 609 381 912. x 72 ª 2. 23. 1036. x 72 average # of stars in a galaxis = 100 000 000

Enumeration Polya-de-Bruijn theory: Cycle index polynomial • Identify subsets C Í F (usually F = Ÿn) with their characteristic function c. C: F ® 2={0, 1} • For a permutation g in the group G Í Aff*(F), we have cycle index cyc(g) = (c 1, …cf), f = #F • Take indeterminates X 1, …Xf, set Xg = X 1 c 1. . . Xf cf • Cycle index polynomial is Z(G) = (#G)-1 SG Xg

Enumeration Polya-de-Bruijn theory: Configuration counting series • Consider polynomial Polya weights w(0), w(1) in –[x] • For c: F ® 2, we have G-invariant product pw(c) = PFw(c(t)) • The configuration counting series is C(G, F, w) = S 2 F/G pw(c)

Enumeration Facts • For w(0) = 1, w(1) = x, the xk coefficient of C(G, F, w) is the number of G-orbits of k-element sets in F • For the constant weight w(0) = w(1) = 1, C(G, F, w) = # 2 F/G (Main) Theorem • C(G, F, w) = Z(G)(w(0)+w(1), w(0)2+w(1) 2, …, w(0)f+w(1)f) Corollary • # 2 F/G = Z(G)(2, 2, …, 2)

Enumeration From generalizations of the main theorem by N. G. de Bruijn, we have (for example) the following enumerations: k= 0 1 2 3 4 5 6 7 8 9 10 11 12 T 12 1 1 6 19 43 66 80 66 43 19 6 1 1 TI 12 1 1 6 12 29 38 50 38 29 12 6 1 1 Aff*(Ÿ 12) 1 1 5 9 21 25 34 25 21 9 5 1 1 k 2 3 4 5 6 # of orbits of (k, 12)-series 6 30 275 2 000 14 060 k 7 8 9 10 11 12 # of orbits of (k, 12)-series 83 280 416 880 1 663 680 4 993 440 9 980 160 9 985 920 (dodecaphonic)

Local Techniques Categories of local compositions • Fix commutative ring R • For any two (left) R-modules A, B, let A@B = e. B. Lin(A, B) be the R-module of R-affine morphisms F(a) = eb. F 0(a) = b + F 0(a) F 0 = linear part, eb = translation part • The category Loc. R of local compositions over R has as objects the couples (K, A) of subsets K of R-modules A, and as morphisms f: (K, A) ® (L, B) set maps f: K ® L which are induced by affine morphism F in A@B.

Local Techniques Local Classification: Calculate the isomorphism classes in Loc. R! For finite local compositions, we have this procedure: • Represent (K, A) by an affine k: Rn ® A with K = {k(e 0), k(e 1), …, k(en)} for #K = n+1 • Then identify K to the orbit k. Sn+1 of the right action of the symmetric group of the affine basis e 0 = 0, e 1, . . . , en • Get rid of the translations within A by taking the linear part k 0 of k, corresponding to the passage to the difference d. K = {k(e 1) - k(e 0), …, k(en) - k(e 0)} • Take the induced right linear action of Sn+1 and the left action of GL(A) on Lin(Rn, A).

Local Techniques Proposition Let Gen(Rn, A) Í Lin(Rn, A) be the subset of difference maps dk: Rn ® A with • dk = surjective • dk(es) π 0 and dk(es) π dk(et) for all s π t. • Take the induced right linear action of Sn+1 and the left action of GL(A) on Gen(Rn, A) Let Lo. Class(A, n+1, R) be the set of isomorphism classes of • local compositions K of cardinality n+1 and ambient space A • K is generating, i. e. A = R. K = Ss, t R. (ks- kt) Then we have a canonical bijection Lo. Class(A, n+1, R) @ GL(A)Gen(Rn, A)/Sn+1

Local Techniques Let Xn(R, A) be the set of submodules V Í Rn with • Rn/V @ A • es, es-et œ V for all s π t together with the above right action of Sn+1 Sending dk: Rn ® A to ker(dk) induces a bijection GL(A)Gen(Rn, A)/Sn+1 @ Xn(R, A)/Sn+1 Let Xn(R, r) be the Sn+1 -stable set of submodules V Í Rn with • Rn/V = locally free of rank r • es, es-et œ V for all s π t Xn(R, r) = Grassn, r(R) - Vn(R, r) = closed, Sn+1 -stable subscheme of Grassn, r(R)

Local Techniques Theorem (local geometric classification) There is a quotient scheme, i. e. , an exact sequence Xn, r ¥ Sn+1 pr 1 m Xn, r /Sn+1 Its R-valued points are the orbits of Xn, r , and if R is semi-simple, Xn, r (R) = Xn(R, r)

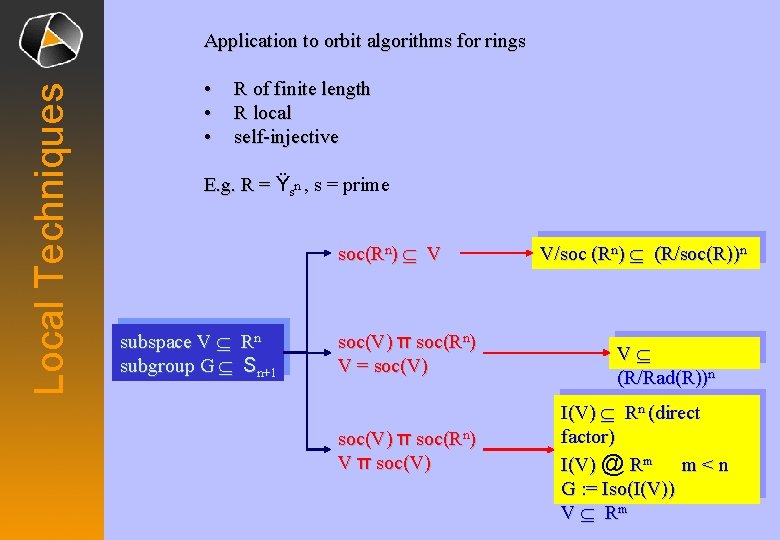
Local Techniques Application to orbit algorithms for rings • • • R of finite length R local self-injective E. g. R = Ÿsn , s = prime soc(Rn) Í V subspace V Í subgroup G Í Rn Sn+1 soc(V) π soc(Rn) V = soc(V) π soc(Rn) V π soc(V) V/soc (Rn) Í (R/soc(R))n VÍ (R/Rad(R))n I(V) Í Rn (direct factor) I(V) @ Rm m < n G : = Iso(I(V)) V Í Rm

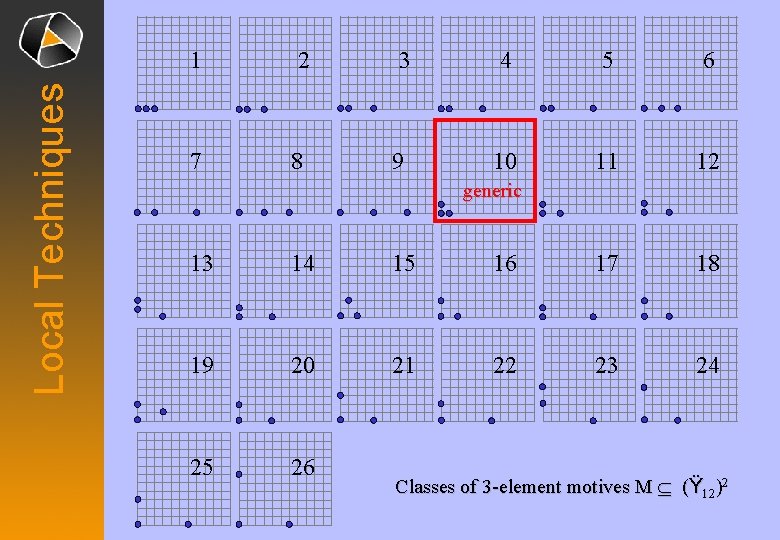
Local Techniques 1 2 3 4 5 6 7 8 9 10 11 12 generic 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Classes of 3 -element motives M Í (Ÿ 12)2

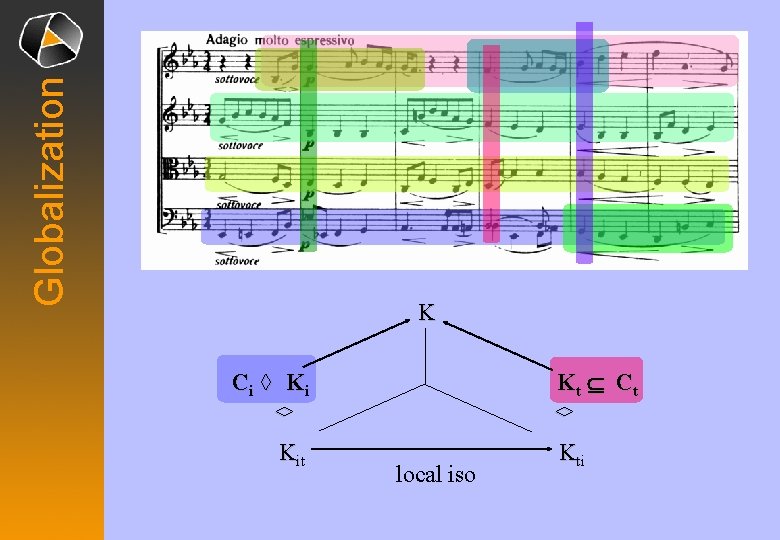
Globalization K K t Í Ct Ci ◊ K i ◊ ◊ Kit local iso Kti

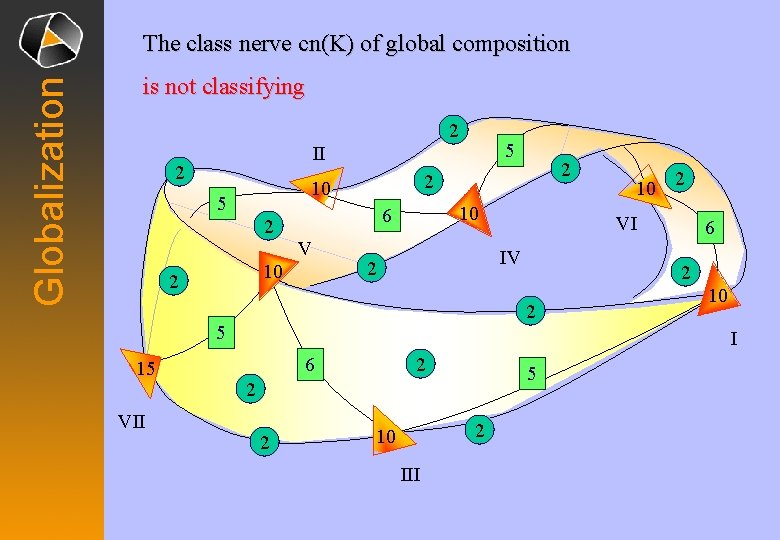
Globalization The class nerve cn(K) of global composition is not classifying 2 5 II 2 10 5 10 2 10 6 2 V VII 10 2 VI IV 2 6 2 2 5 15 2 2 10 I 2 6 5 2 2 2 10 III

Globalization @B MÍ A @B B A = address of the composition (A= R)

Globalization The category Loc. A of local A-addressed compositions has as objects the couples (K, A@C) of sets K of affine morphisms in A@C and as morphisms f: (K, A@C) ® (L, A@D) set maps f: K ® L which are naturally induced by affine morphism F in C@D The category Glob. A of global A-addressed compositions has as objects KI coverings of sets K by atlases I of local Aaddressed compositions with manifold gluing conditions and manifold morphisms ff: KI ® LJ , including and compatible with atlas morphisms f: I ® J ! y f i s s a l C

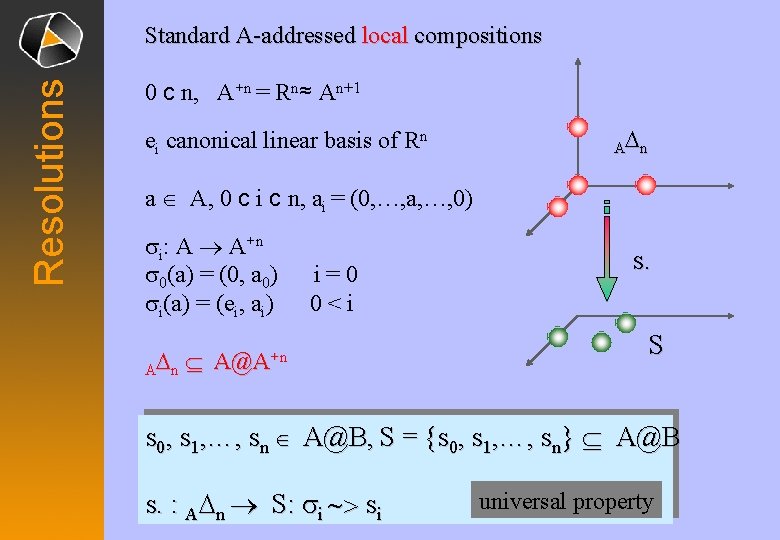
Resolutions Standard A-addressed local compositions 0 c n, A+n = Rn≈ An+1 ei canonical linear basis of Rn AD n a Î A, 0 c i c n, ai = (0, …, a, …, 0) si: A ® A+n s 0(a) = (0, a 0) si(a) = (ei, ai) AD n Í i=0 0<i A@A+n s. S s 0, s 1, …, sn Î A@B, S = {s 0, s 1, …, sn} Í A@B s. : ADn ® S: si ~> si universal property

Resolutions Standard A-addressed global compositions n* = covering of an interval [0, m] by non-empty subsets n* induces a A-addressed global standard composition ADn* which is canonically deduced from ADm by the n*-charts Choose enumeration K = {k 0, k 1, …, km} of the global compostition KI. Call n*(KI) the covering of [0, m] corresponding to the atlas I. DKI = ADn*(KI) is the resolution of KI res(KI): D KI ® K I ◊ ◊ AD m i ® Ki universal morphism, natural in KI

Resolutions Represent KI by module complexes of function in D KI A module complex M on KI is a „coefficient system“ on the nerve n(KI), i. e. a functor • M(s) = R-module for simplex s • affine transition morphisms Ms, t: M(s) ® M(t), s Í t Important Examples: • Function complex n. G(KI): For simplex s, take local composition Ç s = Çs Ki n. G(KI)(s) = Loc. R(Ç s, A@R) • N Í n. G(KI) subcomplex; for morphism ff: LJ ® KI of global compositions, we have induced function complex N÷ff Í n. G( LJ)

Resolutions The resolution complex of KI res(KI): DKI ® KI Dn. G(KI) = n. G(KI)÷res(KI) Classification Strategy: • Reconstruct KI from its resolution complex • Classify a relevant set of module complexes Res. A, n* = {N Í n. G(ADn*), properties…} which relate to resolution complexes of global compositions KI with n*(KI) @ n*

Resolutions Reconstruction of KI • Local construction for simplex s of the resolution ADn* and module N(s): e. N, s: ADs ® A@N(s)* e. N, s(s) (a)(l) = l(s)(a) for a function l in N(s) • Have local compositions s/N = Im(e. N, s) Í A@N(s)*, and canonical local morphisms s/N ® t/N for t Í s • Global construction: ADn*/N = colimn* s/N

Resolutions Proposition 1. Let KI have these properties (*) • the chart modules R. Ki are projective of finite type • the function modules n. G(KI)(Ki) are projective Then I) @ K I D / D n G (K A n* 2. Res. A, n* = {N Í n. G(ADn*), Const Í N N(s 0) = projective of finite type N separates points of ADn* } Then we have a canonical bijection Res. A, n*/Aut(ADn*) @ Iso. Classes[KI with (*) and n*(KI) @ n*]

Resolutions Theorem (global addressed geometric classification) Let A be locally free of a defined rank. Then there is a subscheme Jn* of a projective R-scheme of finite type such that its S-valued points w: Spec(S) ® Jn* are in bijection with the classifying orbits of module complexes N in SƒRADn* which are locally free of defined co-ranks on the zero simplexes of n*. Resn*, r ¥ Aut(ADn*) pr 1 m Resn*, r / Aut(ADn*) = Jn*