Classification Regression Support Vector Machines Jeff Howbert Introduction

Classification / Regression Support Vector Machines Jeff Howbert Introduction to Machine Learning Winter 2012 1

Support vector machines l Topics – SVM classifiers for linearly separable classes – SVM classifiers for non-linearly separable classes – SVM classifiers for nonlinear decision boundaries u kernel functions – Other applications of SVMs – Software Jeff Howbert Introduction to Machine Learning Winter 2012 2

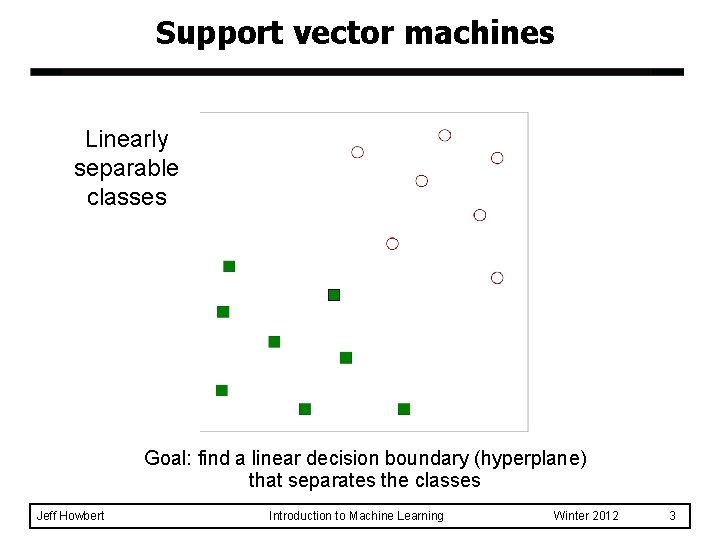
Support vector machines Linearly separable classes Goal: find a linear decision boundary (hyperplane) that separates the classes Jeff Howbert Introduction to Machine Learning Winter 2012 3

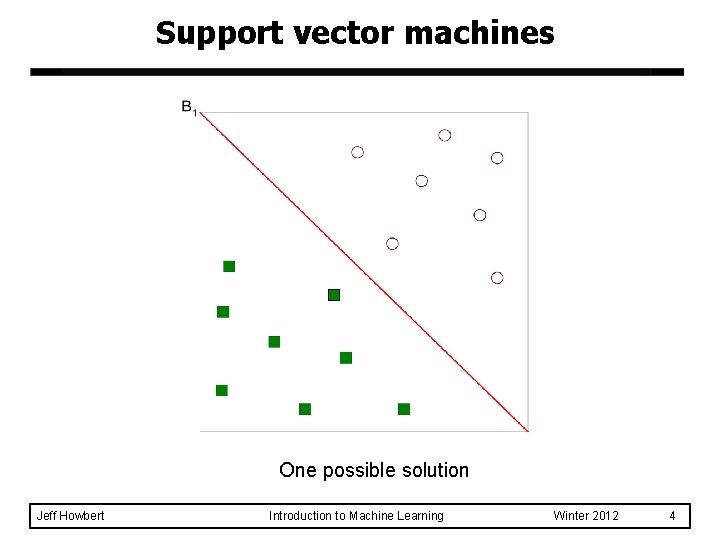
Support vector machines One possible solution Jeff Howbert Introduction to Machine Learning Winter 2012 4

Support vector machines Another possible solution Jeff Howbert Introduction to Machine Learning Winter 2012 5

Support vector machines Other possible solutions Jeff Howbert Introduction to Machine Learning Winter 2012 6

Support vector machines Which one is better? B 1 or B 2? How do you define better? Jeff Howbert Introduction to Machine Learning Winter 2012 7

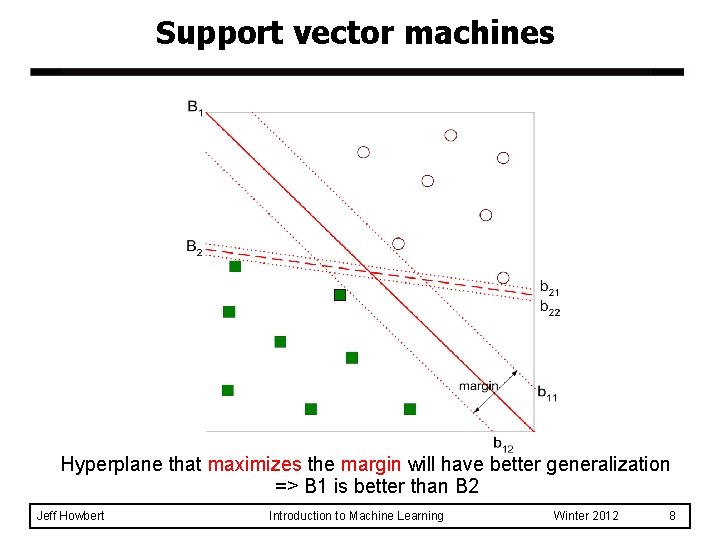
Support vector machines Hyperplane that maximizes the margin will have better generalization => B 1 is better than B 2 Jeff Howbert Introduction to Machine Learning Winter 2012 8

Support vector machines Hyperplane that maximizes the margin will have better generalization => B 1 is better than B 2 Jeff Howbert Introduction to Machine Learning Winter 2012 9

Support vector machines Hyperplane that maximizes the margin will have better generalization => B 1 is better than B 2 Jeff Howbert Introduction to Machine Learning Winter 2012 10

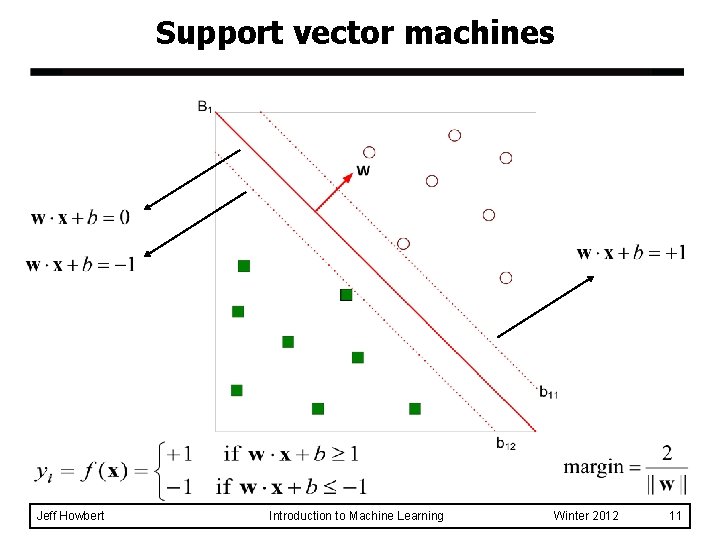
Support vector machines Jeff Howbert Introduction to Machine Learning Winter 2012 11

Support vector machines l We want to maximize: l Which is equivalent to minimizing: l But subject to the following constraints: – This is a constrained convex optimization problem – Solve with numerical approaches, e. g. quadratic programming Jeff Howbert Introduction to Machine Learning Winter 2012 12

Support vector machines Solving for w that gives maximum margin: 1. Combine objective function and constraints into new objective function, using Lagrange multipliers i 2. To minimize this Lagrangian, we take derivatives of w and b and set them to 0: Jeff Howbert Introduction to Machine Learning Winter 2012 13

Support vector machines Solving for w that gives maximum margin: 3. Substituting and rearranging gives the dual of the Lagrangian: which we try to maximize (not minimize). 4. Once we have the i, we can substitute into previous equations to get w and b. 5. This defines w and b as linear combinations of the training data. Jeff Howbert Introduction to Machine Learning Winter 2012 14

Support vector machines l Optimizing the dual is easier. – Function of i only, not i and w. Convex optimization guaranteed to find global optimum. l Most of the i go to zero. l – The xi for which i 0 are called the support vectors. These “support” (lie on) the margin boundaries. – The xi for which i = 0 lie away from the margin boundaries. They are not required for defining the maximum margin hyperplane. Jeff Howbert Introduction to Machine Learning Winter 2012 15

Support vector machines Example of solving for maximum margin hyperplane Jeff Howbert Introduction to Machine Learning Winter 2012 16

Support vector machines What if the classes are not linearly separable? Jeff Howbert Introduction to Machine Learning Winter 2012 17

Support vector machines Now which one is better? B 1 or B 2? How do you define better? Jeff Howbert Introduction to Machine Learning Winter 2012 18

Support vector machines What if the problem is not linearly separable? l Solution: introduce slack variables l – Need to minimize: – Subject to: – C is an important hyperparameter, whose value is usually optimized by cross-validation. Jeff Howbert Introduction to Machine Learning Winter 2012 19

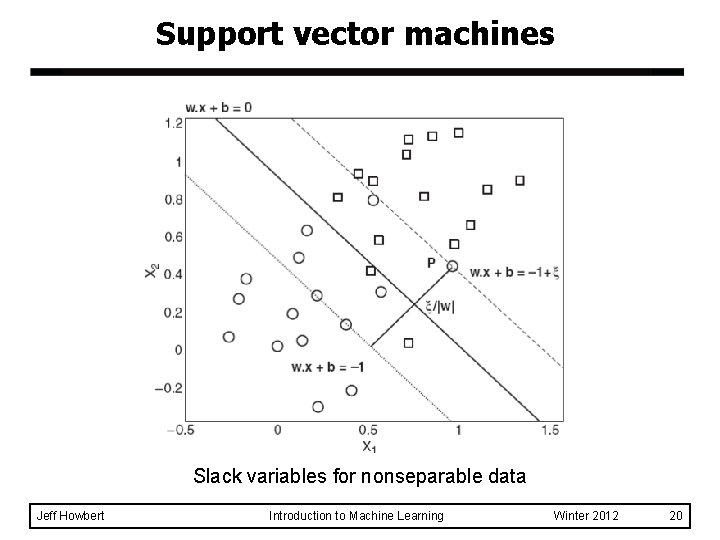
Support vector machines Slack variables for nonseparable data Jeff Howbert Introduction to Machine Learning Winter 2012 20

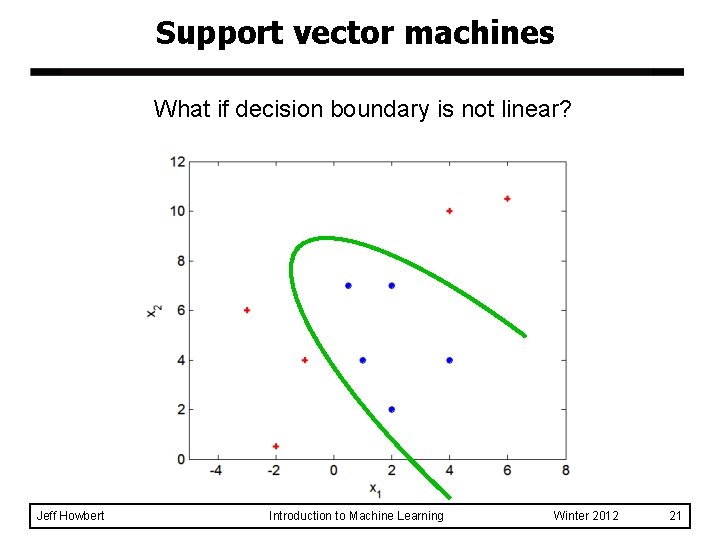
Support vector machines What if decision boundary is not linear? Jeff Howbert Introduction to Machine Learning Winter 2012 21

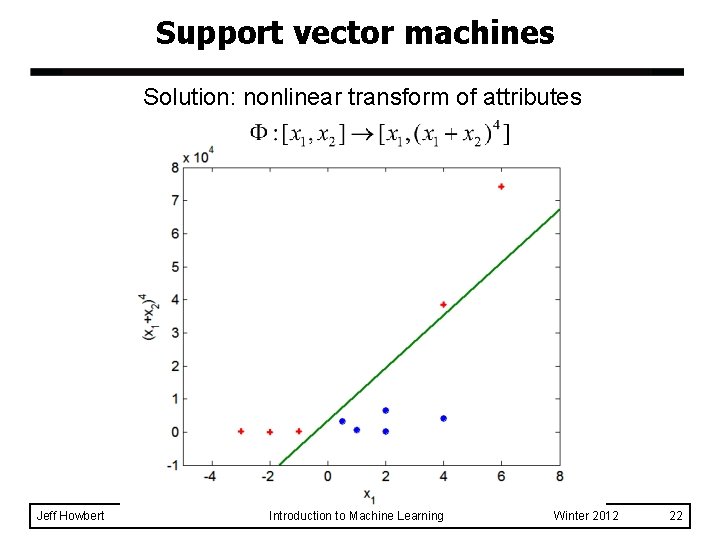
Support vector machines Solution: nonlinear transform of attributes Jeff Howbert Introduction to Machine Learning Winter 2012 22

Support vector machines Solution: nonlinear transform of attributes Jeff Howbert Introduction to Machine Learning Winter 2012 23

Support vector machines l Issues with finding useful nonlinear transforms – Not feasible to do manually as number of attributes grows (i. e. any real world problem) – Usually involves transformation to higher dimensional space l u increases computational burden of SVM optimization u curse of dimensionality With SVMs, can circumvent all the above via the kernel trick Jeff Howbert Introduction to Machine Learning Winter 2012 24

Support vector machines l Kernel trick – Don’t need to specify the attribute transform ( x ) – Only need to know how to calculate the dot product of any two transformed samples: k( x 1, x 2 ) = ( x 1 ) ( x 2 ) – The kernel function k is substituted into the dual of the Lagrangian, allowing determination of a maximum margin hyperplane in the (implicitly) transformed space ( x ) – All subsequent calculations, including predictions on test samples, are done using the kernel in place of ( x 1 ) ( x 2 ) Jeff Howbert Introduction to Machine Learning Winter 2012 25

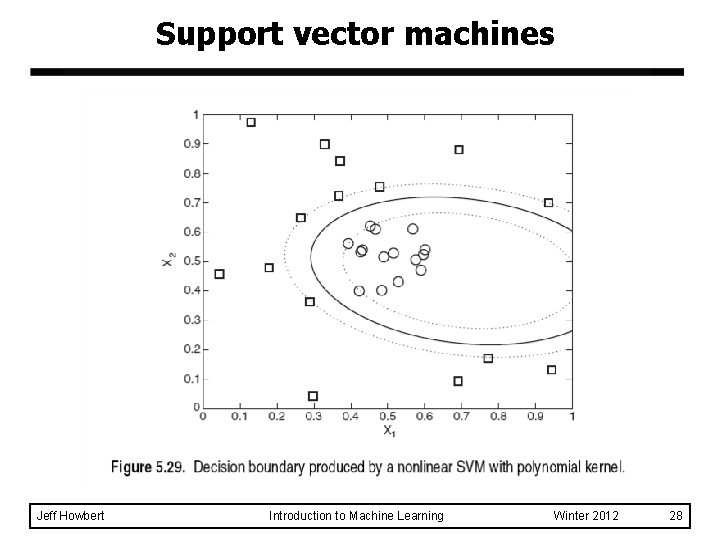
Support vector machines l Common kernel functions for SVM – linear – polynomial – Gaussian or radial basis – sigmoid Jeff Howbert Introduction to Machine Learning Winter 2012 26

Support vector machines l For some kernels (e. g. Gaussian) the implicit transform ( x ) is infinite-dimensional! – But calculations with kernel are done in original space, so computational burden and curse of dimensionality aren’t a problem. Jeff Howbert Introduction to Machine Learning Winter 2012 27

Support vector machines Jeff Howbert Introduction to Machine Learning Winter 2012 28

Support vector machines l Applications of SVMs to machine learning – Classification binary u multiclass u one-class u – – – Regression Transduction (semi-supervised learning) Ranking Clustering Structured labels Jeff Howbert Introduction to Machine Learning Winter 2012 29

Support vector machines l Software – SVMlight u http: //svmlight. joachims. org/ – lib. SVM http: //www. csie. ntu. edu. tw/~cjlin/libsvm/ u includes MATLAB / Octave interface u Jeff Howbert Introduction to Machine Learning Winter 2012 30