Classification Problem Given Predict class label of a

Classification Problem • Given - - -+ ++ + + -- - + ++ + -- + + + - - -. ++ + + - - - ++ ++ - • Predict class label of a given query

Classification Problem • Unknown probability distribution • We need to estimate:

The Bayesian Classifier • Loss function: • Expected loss (conditional risk) associated with class j: • Bayes rule: • Zero-one loss function: Bayes rule

The Bayesian Classifier • Bayes rule achieves the minimum error rate • How to estimate the posterior probabilities:

Density estimation • Use Bayes theorem to estimate the posterior probability values: is the probability density function of class is the prior probability of class given

Naïve Bayes Classifier • Makes the assumption of independence of features given the class: • The task of estimating a q-dimensional density function is reduced to the estimation of q one-dimensional density functions. Thus, the complexity of the task is drastically reduced. • The use of Bayes theorem becomes much simpler. • Proven to be effective in practice.

Nearest-Neighbor Methods • Predict the class label of as the most frequent one occurring in the neighbors - -+ ++ + + -- - + ++ + + -- + + + + + - -+ + - - - ++ ++ - .

Nearest-Neighbor Methods • Predict the class label of as the most frequent one occurring in the neighbors - -+ ++ + + -- - + ++ + + -- + + + + + - -- + + + - - - ++ ++ -

Nearest-Neighbor Methods • Predict the class label of as the most frequent one occurring in the neighbors - -+ ++ + + -- - + ++ + + -- + + + + + - -+ + - - - ++ ++ - . . Basic assumption: . e c n a t s di metric

Example: Letter Recognition First statistical moment . . . Edge count

Asymptotic Properties of K-NN Methods if and • The first condition reduces the variance by making the estimation independent of the accidental characteristics of the K nearest neighbors. • The secondition reduces the bias by assuring that the K nearest neighbors are arbitrarily close to the query point.

Asymptotic Properties of K-NN Methods classification error rate of the 1 -NN rule classification error rate of the Bayes rule In the asymptotic limit no decision rule is more than twice as accurate as the 1 -NN rule

Finite-sample settings • How well the 1 -NN rule works in finitesample settings? • If the number of training data N is large and the number of input features q is small, then the asymptotic results may still be valid. • However, for a moderate to large number of input variables, the sample required for their validity is beyond feasibility.

Curse-of-Dimensionality • This phenomenon is known as the curse-of-dimensionality • It refers to the fact that in high dimensional spaces data become extremely sparse and are far apart from each other • It affects any estimation problem with high dimensionality

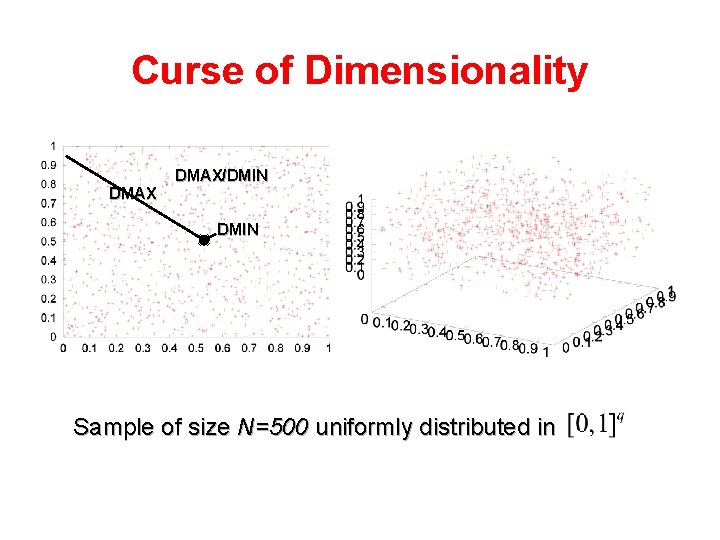
Curse of Dimensionality DMAX/DMIN Sample of size N=500 uniformly distributed in

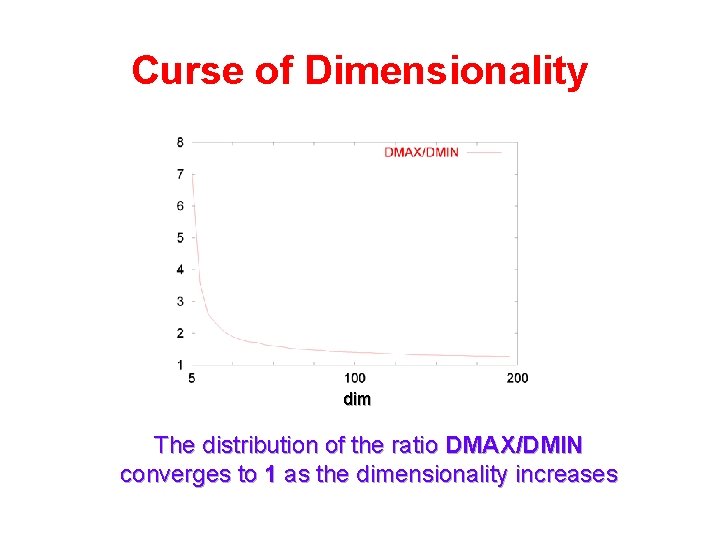
Curse of Dimensionality dim The distribution of the ratio DMAX/DMIN converges to 1 as the dimensionality increases

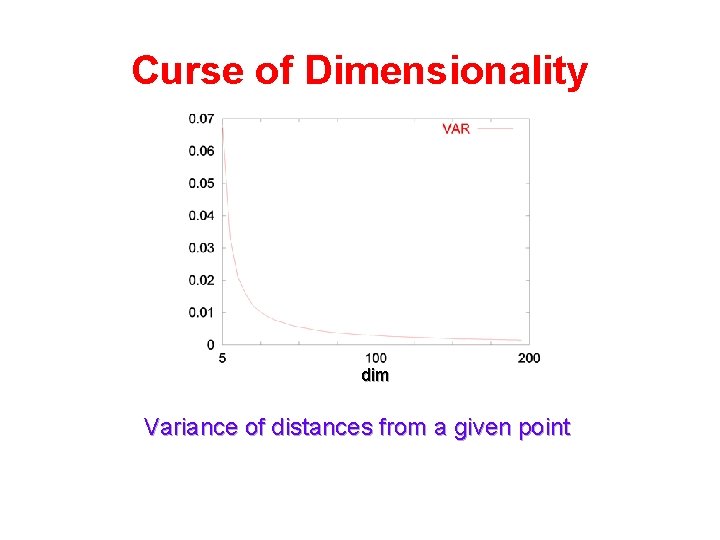
Curse of Dimensionality dim Variance of distances from a given point

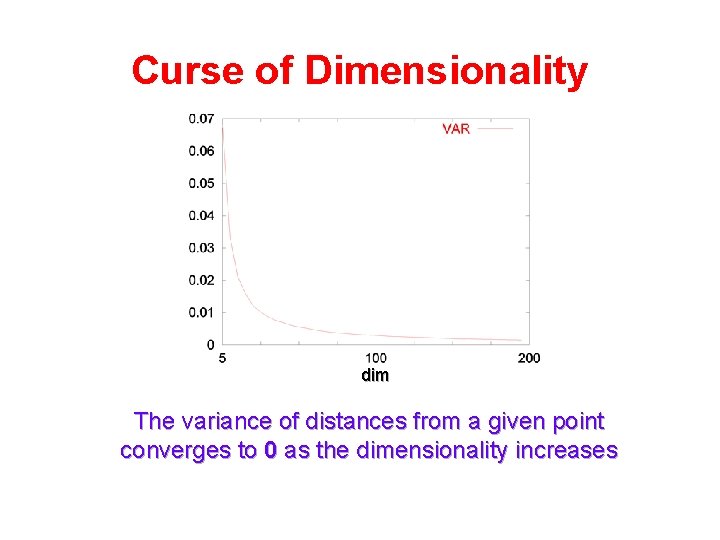
Curse of Dimensionality dim The variance of distances from a given point converges to 0 as the dimensionality increases

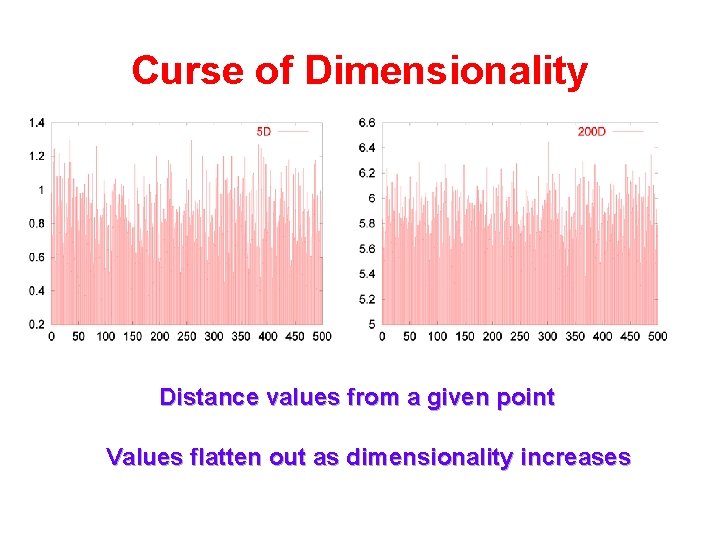
Curse of Dimensionality Distance values from a given point Values flatten out as dimensionality increases

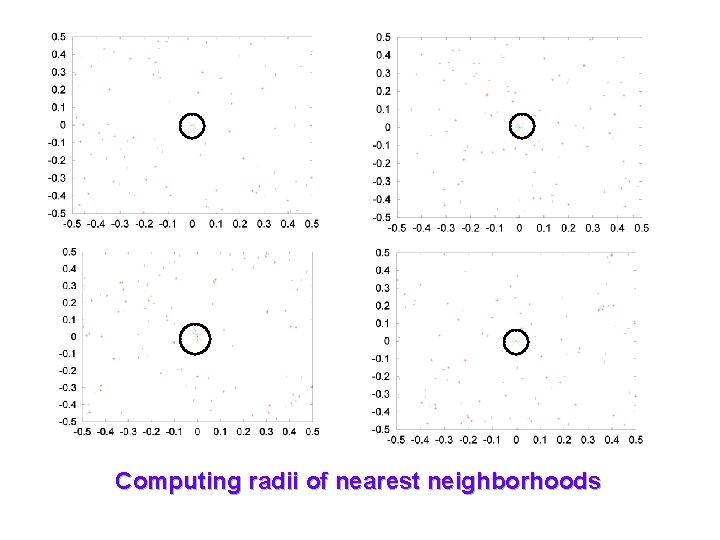
Computing radii of nearest neighborhoods

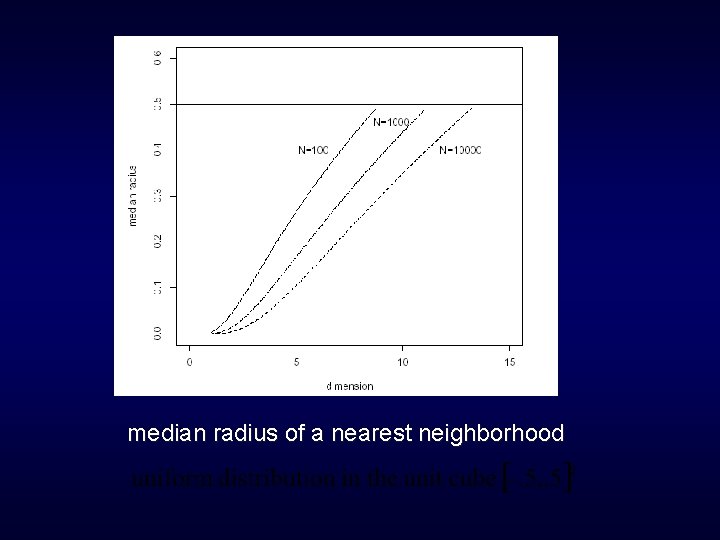
median radius of a nearest neighborhood

Curse-of-Dimensionality As dimensionality increases, the distance from the closest point increases faster • Random sample of size uniform distribution in the -dimensional unit hypercube • Diameter of a distance: Large neighborhood using Euclidean Highly biased estimations

Curse-of-Dimensionality • It is a serious problem in many real-world applications • Microarray data: 3, 000 -4, 000 genes; • Documents: 10, 000 -20, 000 words in dictionary; • Images, face recognition, etc.

How can we deal with the curse of dimensionality?

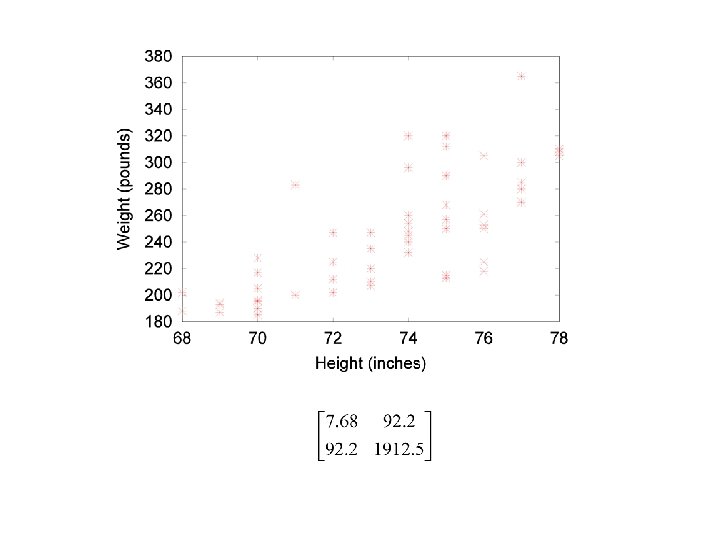
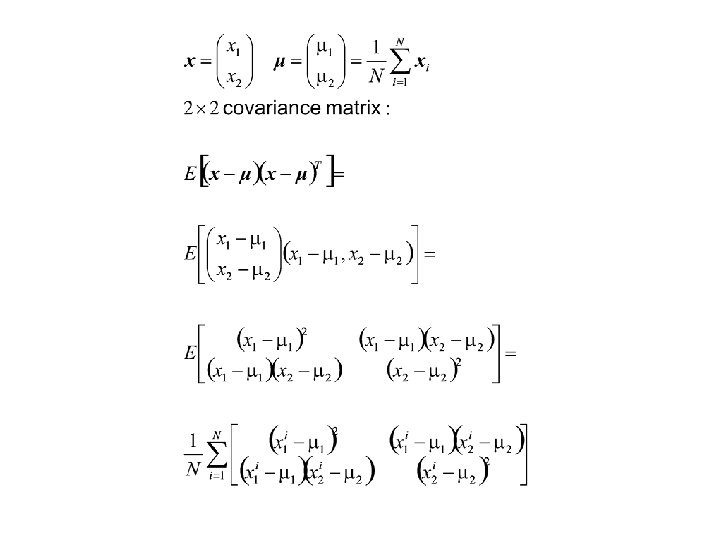
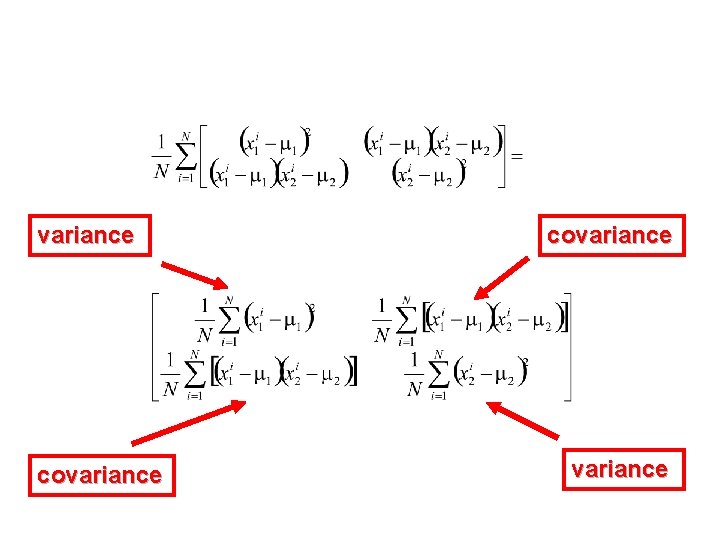
variance covariance

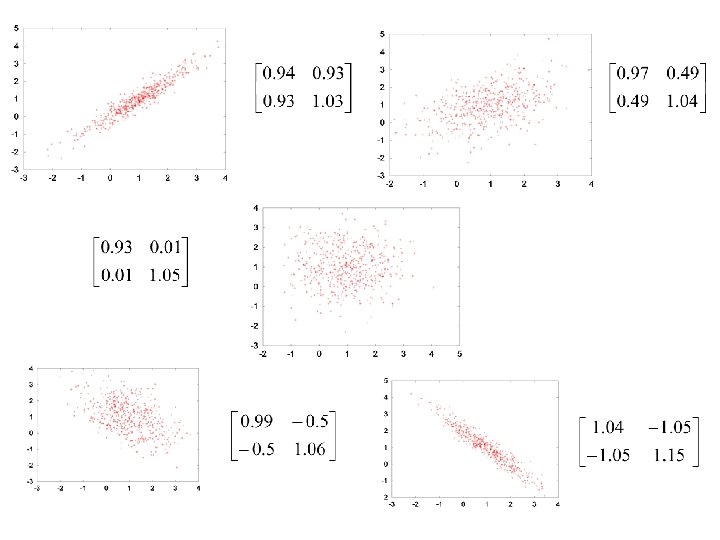
Dimensionality Reduction • Many dimensions are often interdependent (correlated); We can: • Reduce the dimensionality of problems; • Transform interdependent coordinates into significant and independent ones;