Classification of the Real Number System Real Rational

Classification of the Real Number System

Real Rational Not Real Irrational Rational - any number that can be written as the ratio of two integers, which consequently can be expressed as a terminating or repeating decimal. Irrational - numbers that cannot be written as a ratio of two integers.

Real Rational Irrational Integers are positive and negative whole numbers and zero such as … -4, -3, -2, -1, 0, 1, 2, 3, 4 and so on. Important Tip Integers do not have any fractional parts. So numbers such a ½, . 3, 2 ¼ , 25% etc are not integers because they involve fractional parts.

Also … When determining if a number is rational the number must be able to be written in such a way that the numerator and denominator is a positive or negative whole number. Additionally … The numerator can be zero but not the denominator.
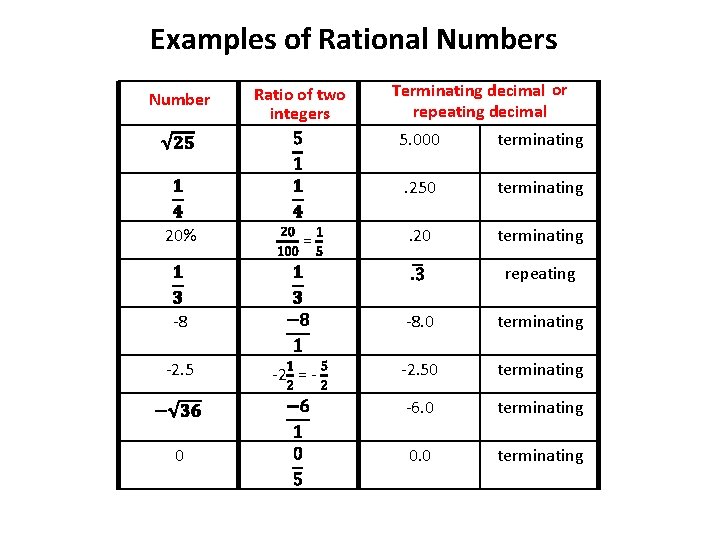
Examples of Rational Numbers Number 20% Ratio of two integers = Terminating decimal or repeating decimal 5. 000 terminating . 250 terminating . 20 terminating repeating -8 -2. 5 0 -2 = - -8. 0 terminating -2. 50 terminating -6. 0 terminating 0. 0 terminating

• The set of rational numbers has subsets • Some common subsets of rational numbers are • Natural/counting numbers • Whole numbers • Integers • Some numbers fall into more than one category
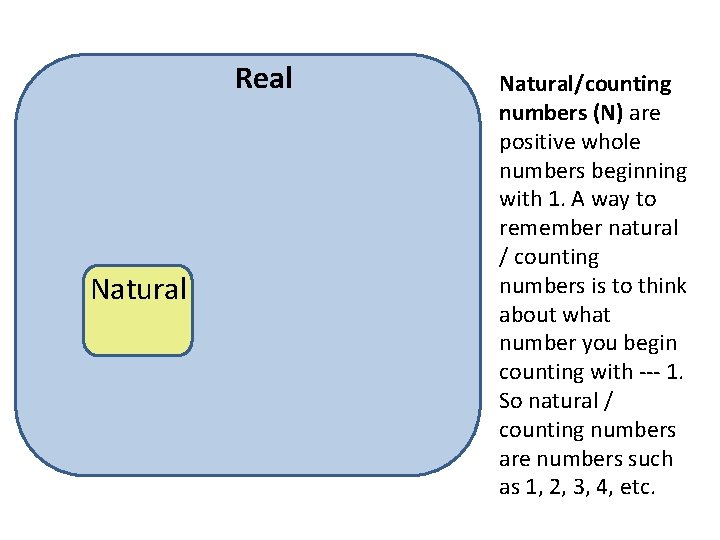
Real Natural/counting numbers (N) are positive whole numbers beginning with 1. A way to remember natural / counting numbers is to think about what number you begin counting with --- 1. So natural / counting numbers are numbers such as 1, 2, 3, 4, etc.
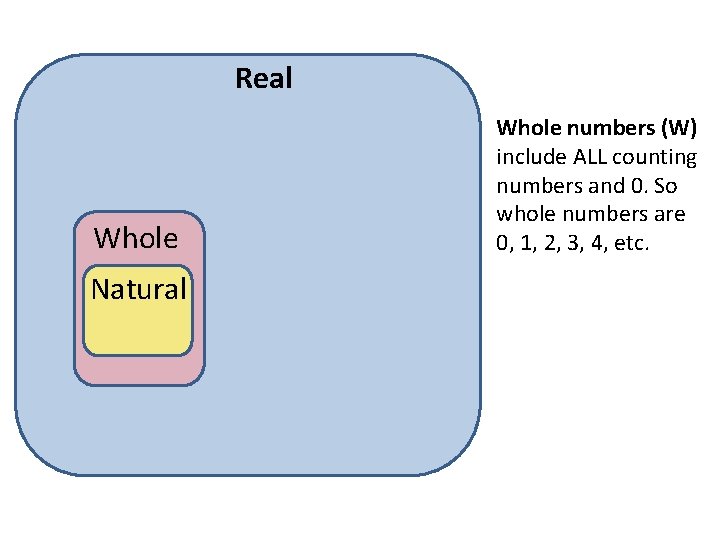
Real Whole Natural Whole numbers (W) include ALL counting numbers and 0. So whole numbers are 0, 1, 2, 3, 4, etc.
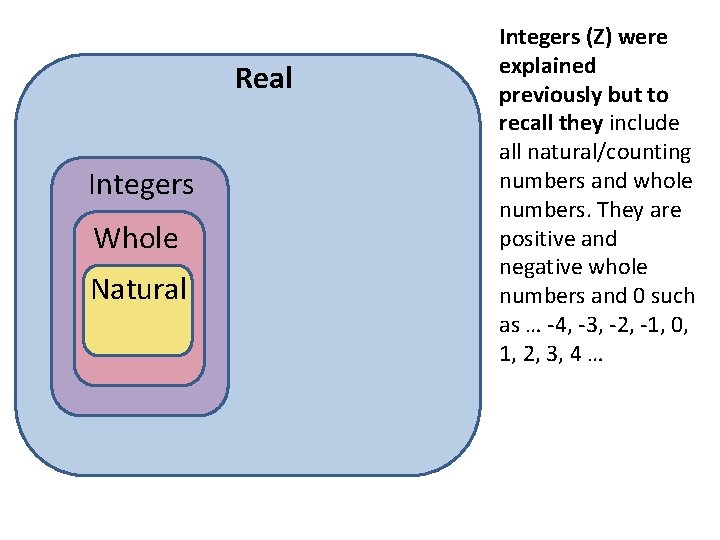
Real Integers Whole Natural Integers (Z) were explained previously but to recall they include all natural/counting numbers and whole numbers. They are positive and negative whole numbers and 0 such as … -4, -3, -2, -1, 0, 1, 2, 3, 4 …
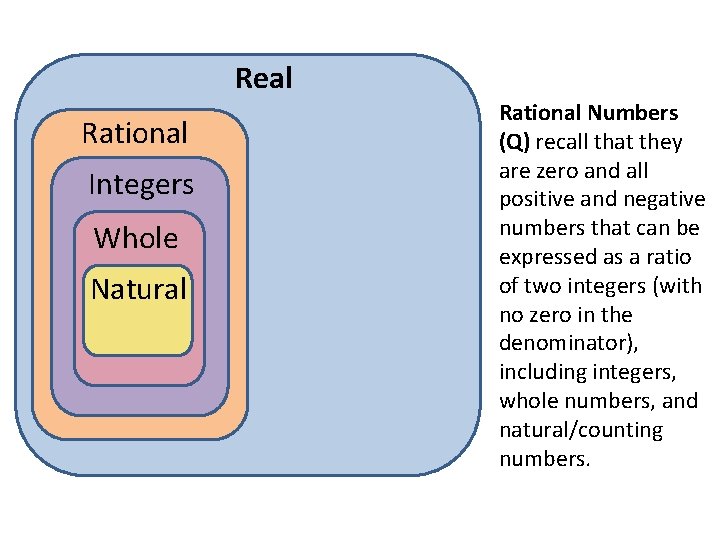
Real Rational Integers Whole Natural Rational Numbers (Q) recall that they are zero and all positive and negative numbers that can be expressed as a ratio of two integers (with no zero in the denominator), including integers, whole numbers, and natural/counting numbers.
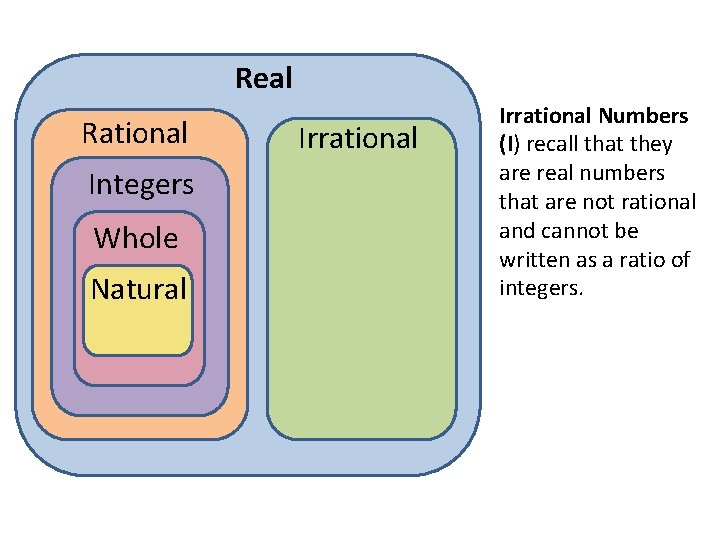
Real Rational Integers Whole Natural Irrational Numbers (I) recall that they are real numbers that are not rational and cannot be written as a ratio of integers.

Examples of Irrational Numbers Pi �� 3. 1415926535897932 384626433832795… 4. 47213594… (and more) 0. 8660254… Irrational numbers are considered real numbers. The real number system can be divided into two categories – rational and irrational. Many students tend to think that irrational numbers are not real. This is not true. Irrational numbers ARE real but just are expressed differently than rational numbers.

Basically in order to determine if a number is real, ask yourself if the numbers can be placed on a number line. If the number can be placed on a number line or be ordered, then the number is real.
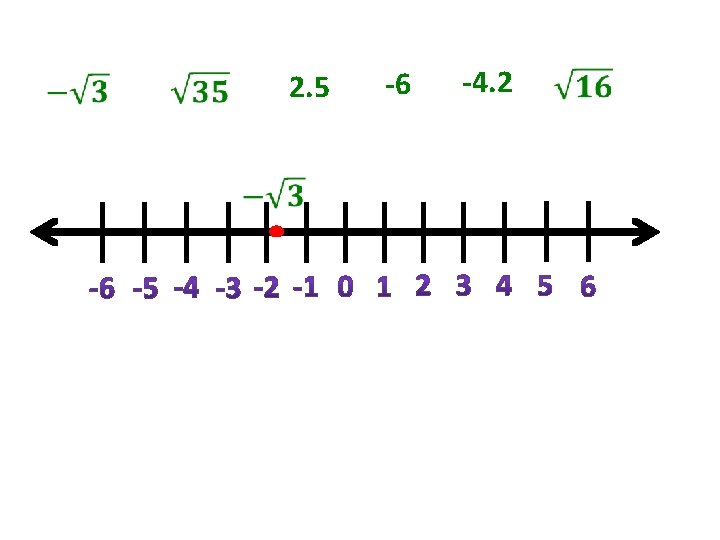
2. 5 -6 -4. 2
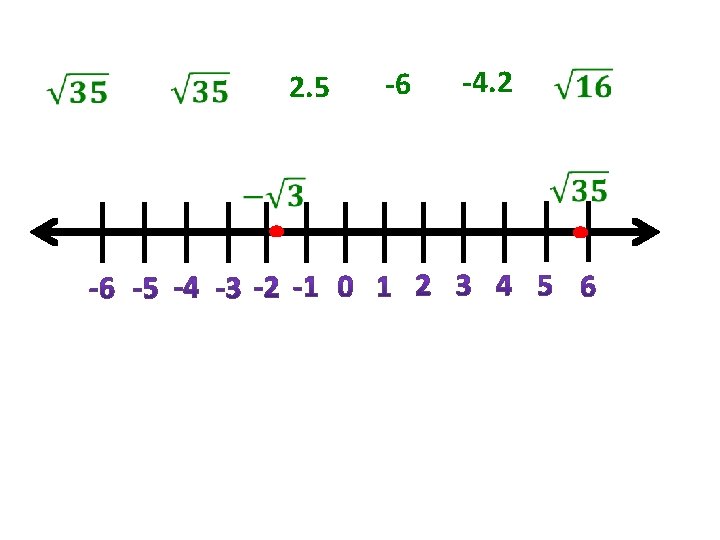
2. 5 -6 -4. 2
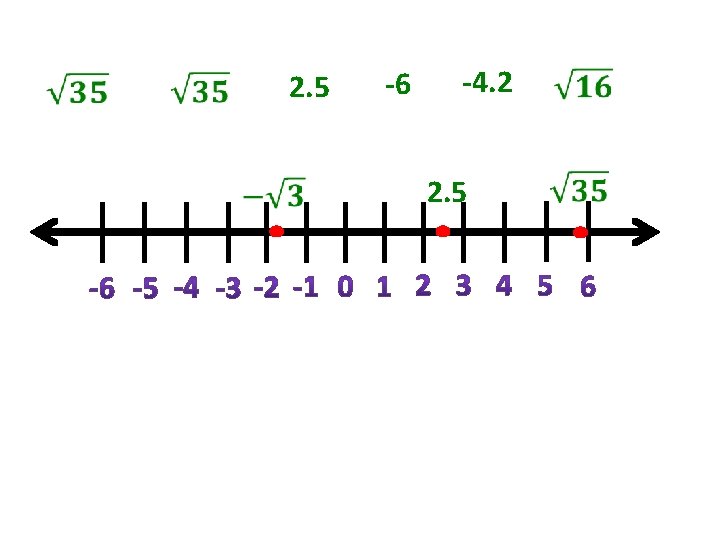
2. 5 -6 -4. 2 2. 5
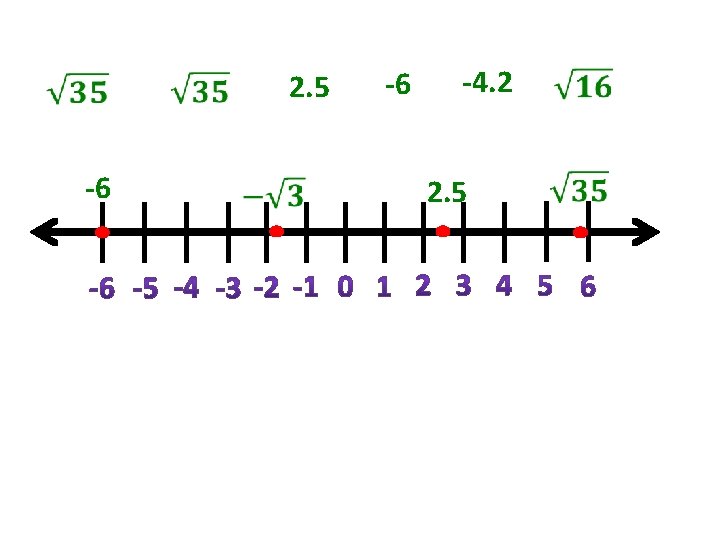
2. 5 -6 -6 -4. 2 2. 5
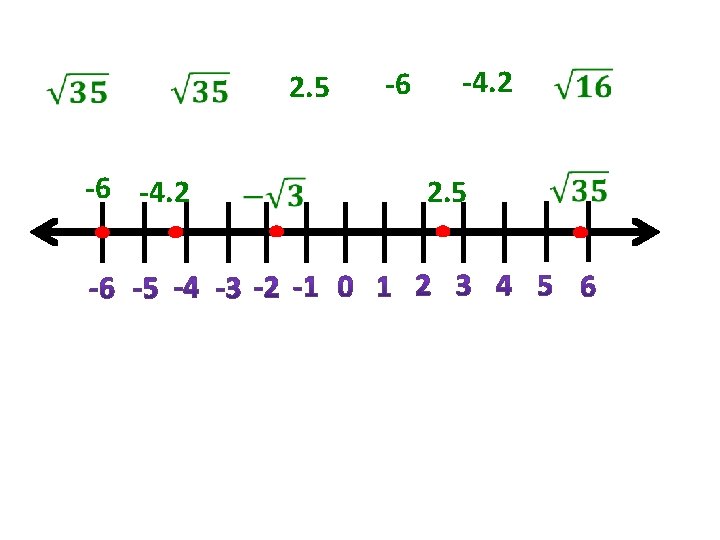
2. 5 -6 -4. 2 2. 5
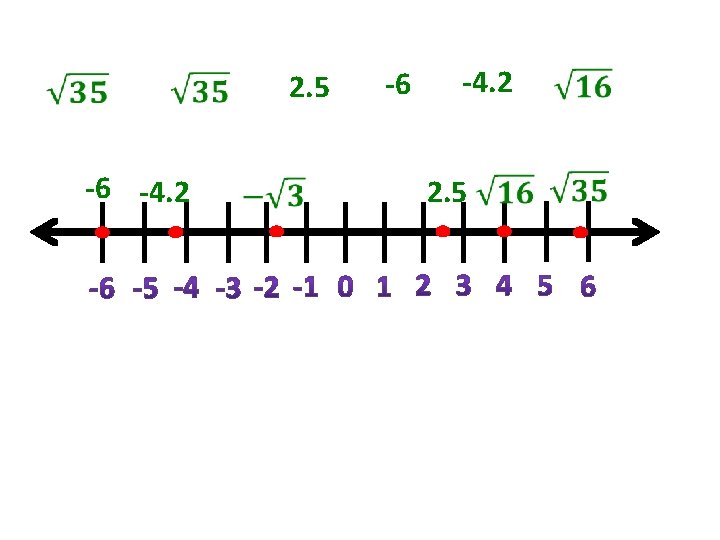
2. 5 -6 -4. 2 2. 5

Numbers Not Considered Real The square root of any negative number are numbers not considered real. These numbers are undefined because zero is in the denominator and cannot be considered a real number. They are not numbers at all.
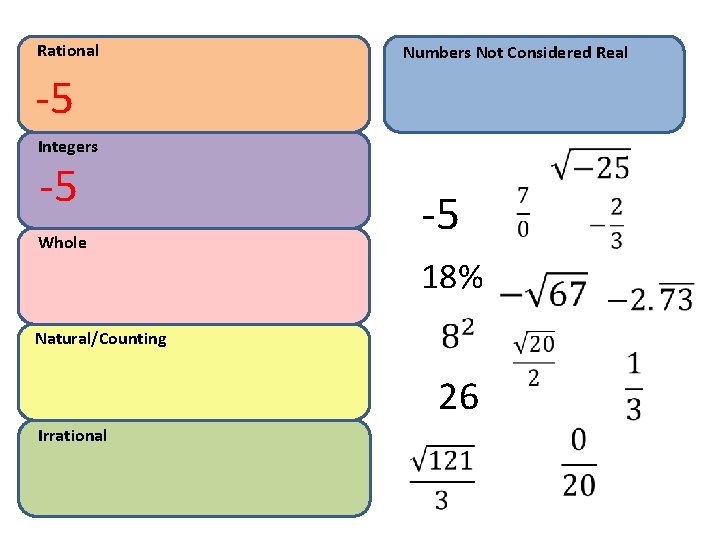
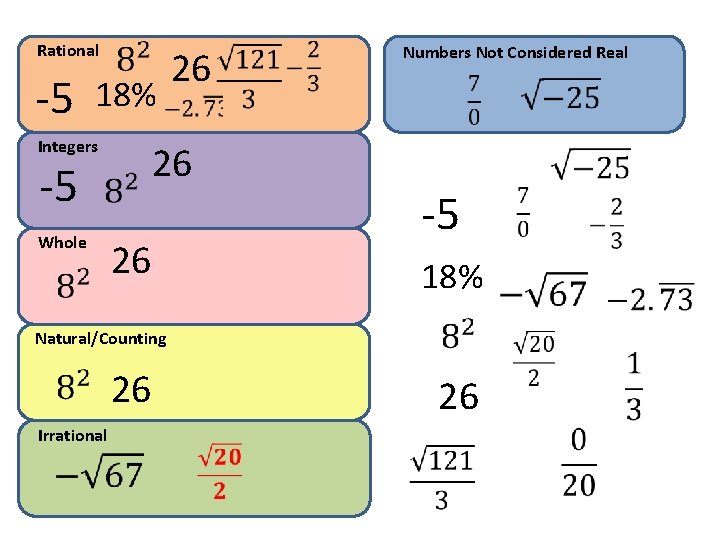
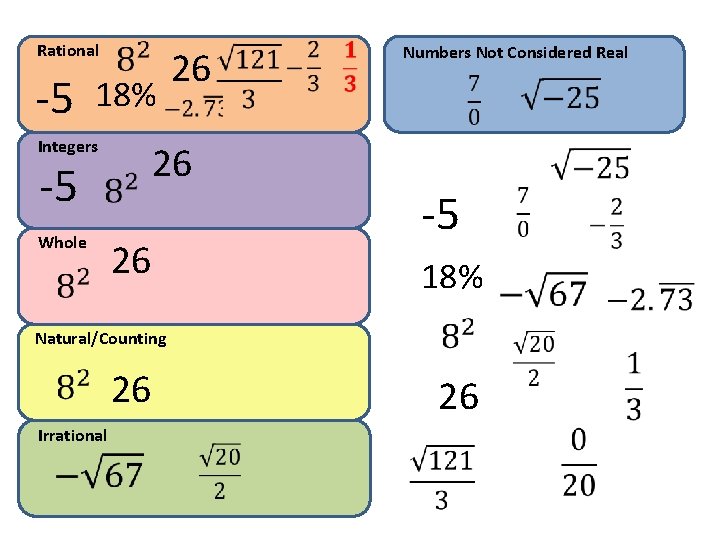
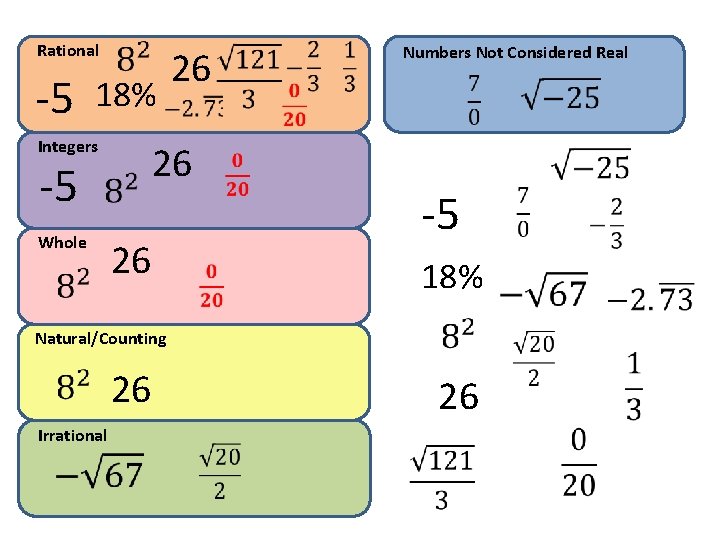
Rational Numbers Not Considered Real -5 Integers -5 Whole -5 18% Natural/Counting 26 Irrational
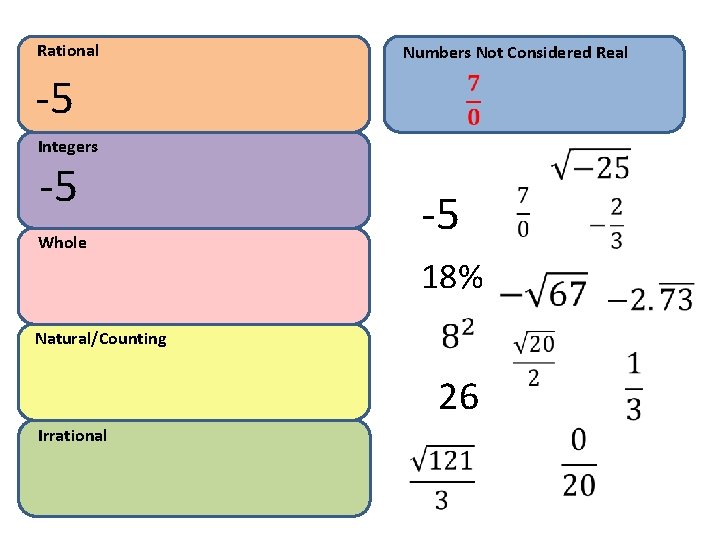
Rational Numbers Not Considered Real -5 Integers -5 Whole -5 18% Natural/Counting 26 Irrational

Rational -5 Numbers Not Considered Real 18% Integers -5 Whole -5 18% Natural/Counting 26 Irrational
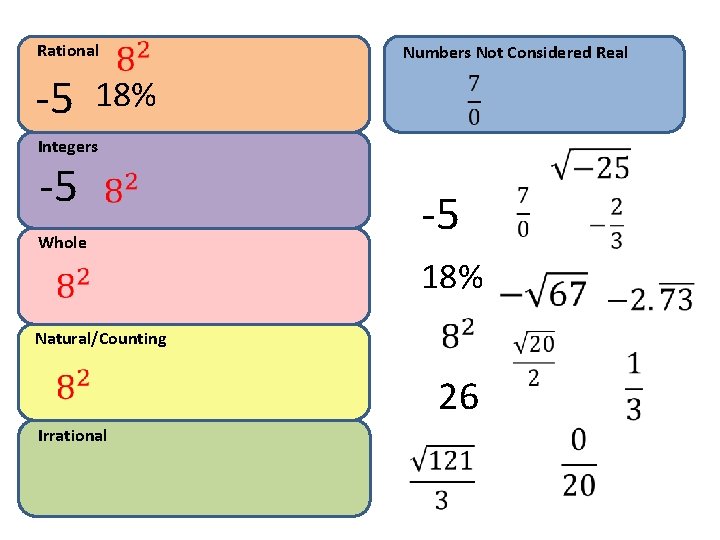
Rational -5 Numbers Not Considered Real 18% Integers -5 Whole -5 18% Natural/Counting 26 Irrational
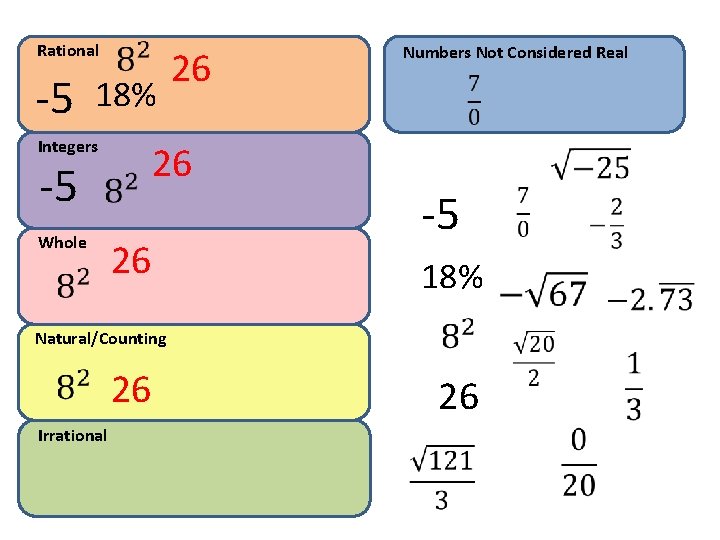
Rational -5 18% Integers 26 -5 Whole 26 26 Numbers Not Considered Real -5 18% Natural/Counting 26 Irrational 26
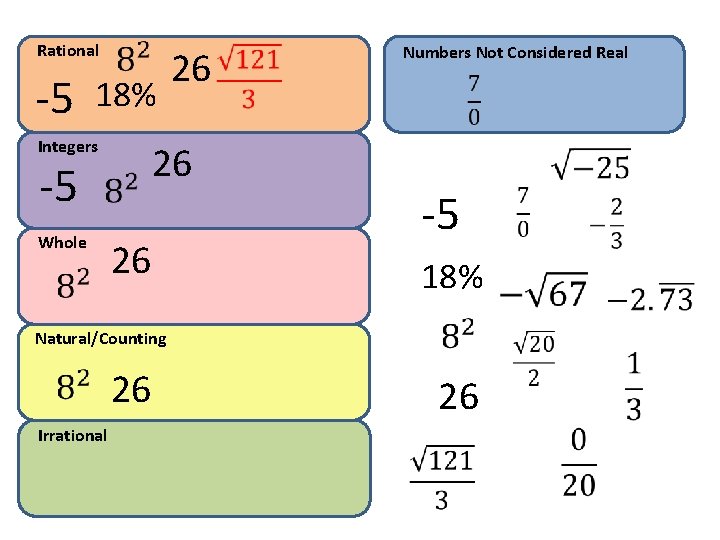
Rational -5 18% Integers 26 -5 Whole 26 26 Numbers Not Considered Real -5 18% Natural/Counting 26 Irrational 26
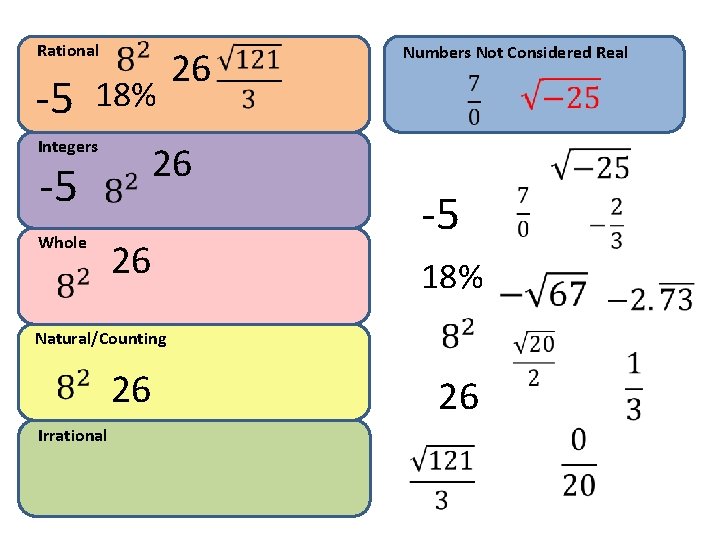
Rational -5 18% Integers 26 -5 Whole 26 26 Numbers Not Considered Real -5 18% Natural/Counting 26 Irrational 26
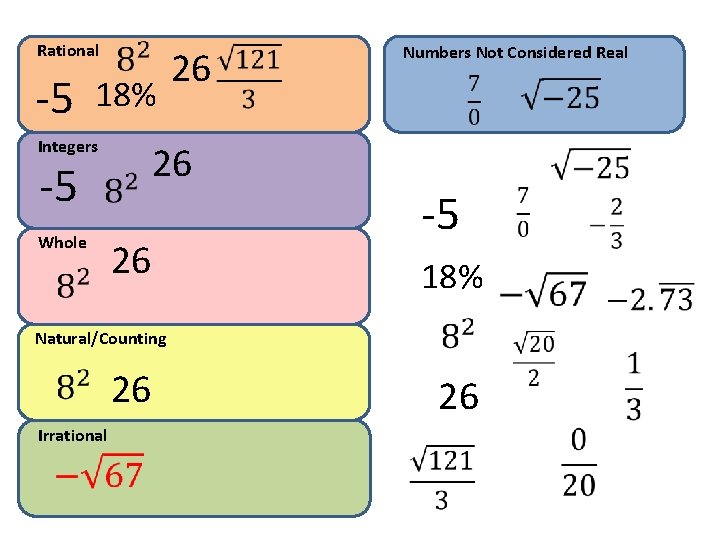
Rational -5 18% Integers 26 -5 Whole 26 26 Numbers Not Considered Real -5 18% Natural/Counting 26 Irrational 26
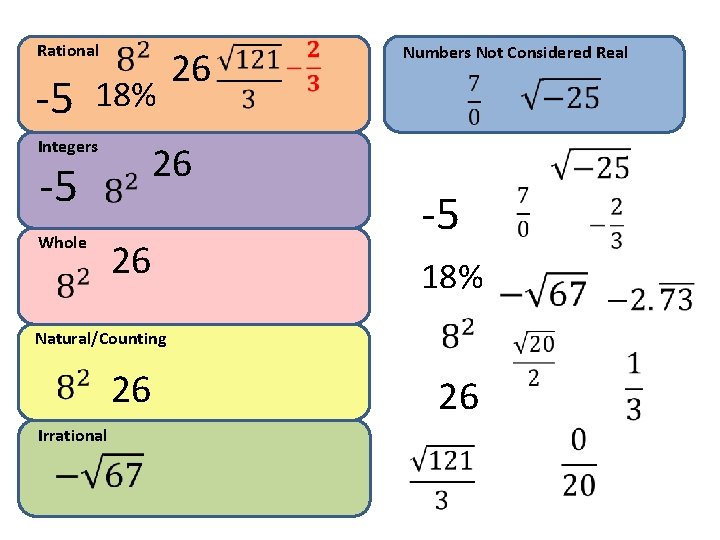
Rational -5 18% Integers 26 -5 Whole 26 26 Numbers Not Considered Real -5 18% Natural/Counting 26 Irrational 26

Rational -5 18% Integers 26 -5 Whole 26 26 Numbers Not Considered Real -5 18% Natural/Counting 26 Irrational 26
Rational -5 18% Integers 26 -5 Whole 26 26 Numbers Not Considered Real -5 18% Natural/Counting 26 Irrational 26
Rational -5 18% Integers 26 -5 Whole 26 26 Numbers Not Considered Real -5 18% Natural/Counting 26 Irrational 26
Rational -5 18% Integers 26 -5 Whole 26 26 Numbers Not Considered Real -5 18% Natural/Counting 26 Irrational 26
- Slides: 33