Classification Linear Models Oliver Schulte Machine Learning 726

Classification: Linear Models Oliver Schulte Machine Learning 726

Continuous Parents, Discrete Child Parent Node/ Child Node Discrete Continuous Discrete Maximum Likelihood Decision Trees logistic regression Continuous conditional Gaussian linear Gaussian (linear regression) 2/57

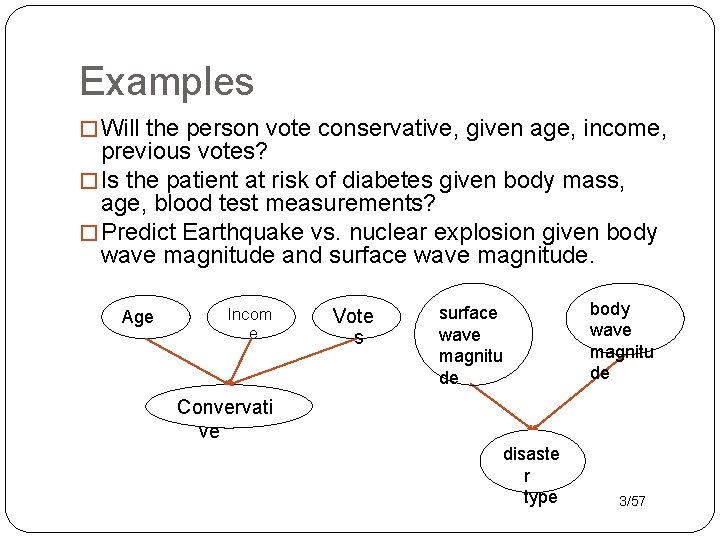
Examples � Will the person vote conservative, given age, income, previous votes? � Is the patient at risk of diabetes given body mass, age, blood test measurements? � Predict Earthquake vs. nuclear explosion given body wave magnitude and surface wave magnitude. Age Incom e Vote s surface wave magnitu de body wave magnitu de Convervati ve disaste r type 3/57

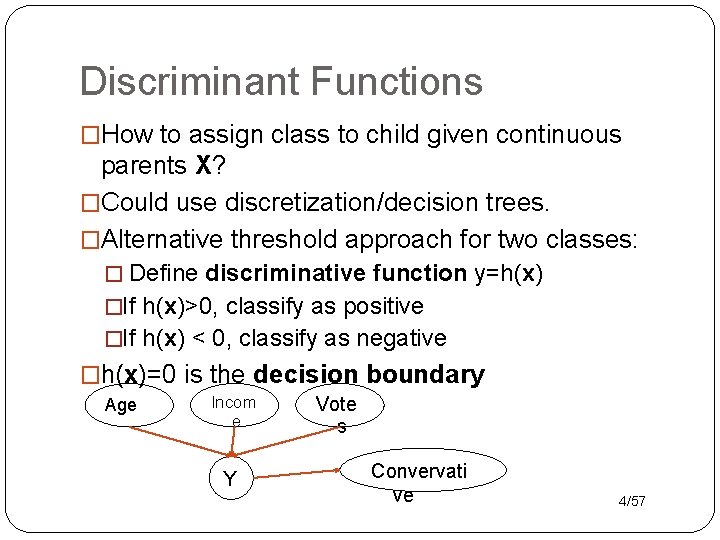
Discriminant Functions �How to assign class to child given continuous parents X? �Could use discretization/decision trees. �Alternative threshold approach for two classes: � Define discriminative function y=h(x) �If h(x)>0, classify as positive �If h(x) < 0, classify as negative �h(x)=0 is the decision boundary Age Incom e Y Vote s Convervati ve 4/57

Advantages �Can use regression ideas about predicting continuous quantities �E. g. regularization 5/57

Log-Odds Classifiers Discriminant Functions for Probabilistic Classifiers

Log-Odds Classifier � For a probabilistic classifier, a natural discriminative function are the log-odds h(x)=ln{P(class=1|x)/P(class=0|x)} � max probability classifier 0 log-odds threshold: �class =1 if P(class=1|x)> P(class=0|x) Ø P(class=1|x)/P(class=0|x)>1 Ø ln{P(class=1|x)/P(class=0|x)}>0 � Log-odds focus on features that discriminate the classes �e. g. P(x) in Bayes formula cancels out �in Naive Bayes, if P(xi|class=1)= P(xi|class=0), then ln{P(xi|class=1)/P(xi|class=0)}=0 Ø non-discriminative features are ignored 7/57

From Log-Odds to Probabilities �Given a class probability distribution, we can compute the class log-odds. �The converse is true as well: we can map class log-odds to class probabilities �Exercise: Show the following implication for the class odds: 8/57

The Logistic Sigmoid Function �Definition: �Squeezes the real line into [0, 1]. �Differentiable: (nice exercise) 9/57

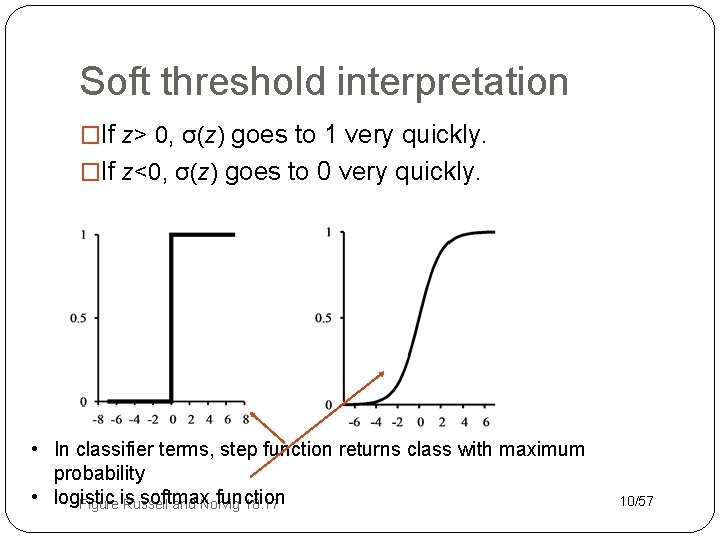
Soft threshold interpretation �If z> 0, σ(z) goes to 1 very quickly. �If z<0, σ(z) goes to 0 very quickly. • In classifier terms, step function returns class with maximum probability • logistic softmax function Figure is Russell and Norvig 18. 17 10/57

Linear Classifiers

Linear Discriminants �Simple linear model: �Can drop explicit w 0 if we assume fixed dummy bias. �Decision surface is line, orthogonal to w. �Can use basis functions 12/57

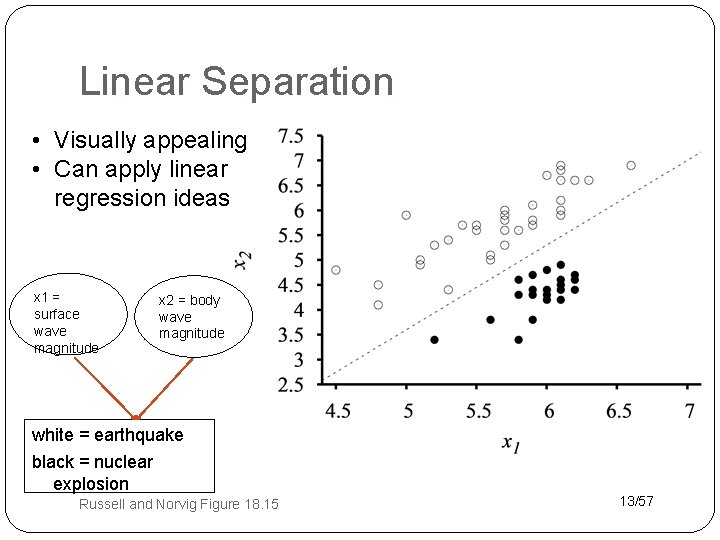
Linear Separation • Visually appealing • Can apply linear regression ideas x 1 = surface wave magnitude x 2 = body wave magnitude white = earthquake black = nuclear explosion Russell and Norvig Figure 18. 15 13/57

Example: Naive Bayes Classifier �Recall the log-odds version of Naive Bayes ln{P(class=1|x)/P(class=0|x)}= Σiln{P(xi|class=1)/P(xi|class=0)}+ln{P(class=1)/P(class=0 )} � Uses learned basis functions (which? ) but no weights Ø cannot weight the influence of different features 14/57

Logistic Regression �LR = linear classifier for log-odds �hw(x) = ln{P(class=1|x)/P(class=0|x)}= x w+w 0 15/57

Example logistic regression model probability of earth quake Figure Russell and Norvig 18. 17 16/57

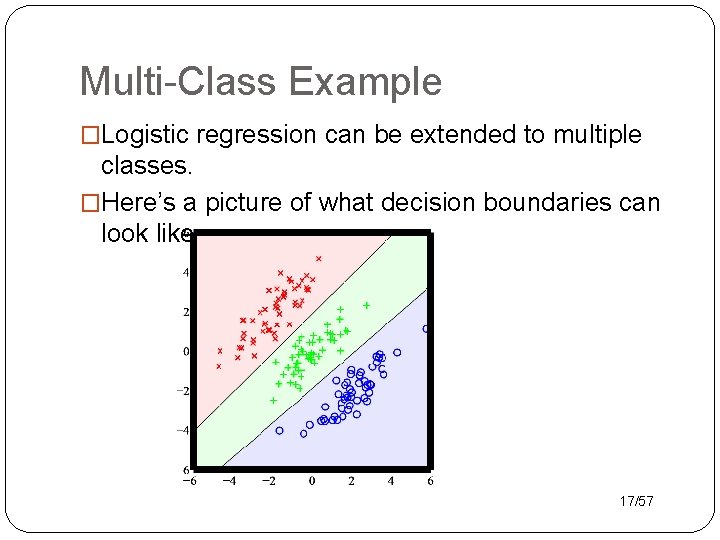
Multi-Class Example �Logistic regression can be extended to multiple classes. �Here’s a picture of what decision boundaries can look like. 17/57

Weight Optimization �Let g denote the logistic function and let y denote the class label. �The L 2 loss can then be defined as • Exercise: find the gradient of the L 2 loss • The bad news: No closed form minimum since g is non-linear function of input features. • The good news: Computer science has many methods to optimize functions without closed-form solutions Hint: recall that 18/57

Gradient Descent

Local Search �Local search method: start somewhere, keep improving, hope to hit on an optimal solution. �Start where? �Good question. The answer is often left up to the user. �Can also try random starting points. (more later) �Keep improving: how? �Simplest answer: follow the gradient of the objective function �Very general method, simple to compute �But usually not the best optimization method �Used extensively to train neural nets 20/57

Gradient Descent: Choosing a direction. �Intuition: think about trying to find street number 1000 on a block. You stop and see that you are at number 100. Which direction should you go, left or right? �You initially check every 50 houses or so where you are. What happens when you get closer to the goal 1000? �The fly and the window: the fly sees that the wall is darker, so the light gradient goes down: bad direction. 21/57

Gradient Descent in One Dimension � Update Rule x : = x – α f'(x) where α is a step size Example: � Try to find y that minimizes f(y) = y 2. � Your current location is y = -3. � What is f’(y)? � Answer: the derivative function is 2 y. � Evaluated at the location -3, the derivative is = -6. � To minimize, we move in the opposite direction -. � Letting the step size α= 1, your new location is -3 – (-6) = -3+6=3 22/57

Gradient Descent In Multiple Dimensions • Fairly Simple Visualization • More complicated examples. 23/57

Gradient Descent: Example. � Try to find x, y that minimizes f(x, y) = 3 x + y 2. � Your current location is x = 10, y = -3. � What is ? ? � Answer: the gradient vector is (3, 2 y). � Evaluated at the location (10, -3), the gradient is = (3, -6). � To minimize, we move in the opposite direction -. � Letting the step size α= 1, your new location is (10, -3) - (3, -6) = (7, 3). 24/57

Gradient Descent: Exercise � Try to find x, y that minimize f(x, y) = 3 x + y 2. � Your current location is x = 7, y = 3. � The gradient vector is (3, 2 y). � Letting the step size α= 1, what is your new location? � Excel Demo 25/57

Stochastic Gradient Descent Formula for Logistic Regression � Stochastic Gradient Descent: Update weights after each single example � Consider example with features x and class label y � General Update Rule for single weight � From exercise, the partial derivative is - xi (y-g(x w)) g(x w) (1 -g(x w)) � So wi : = wi + α xi (y-g(x w)) g(x w) (1 -g(x w)) 26/57

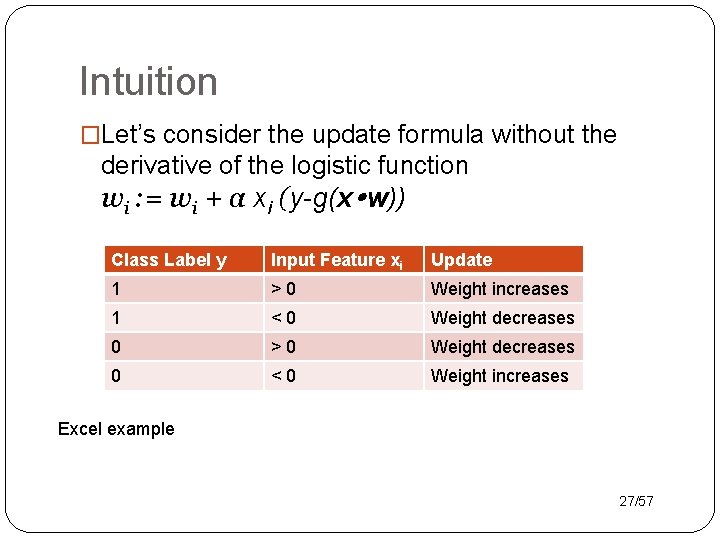
Intuition �Let’s consider the update formula without the derivative of the logistic function wi : = wi + α xi (y-g(x w)) Class Label y Input Feature xi Update 1 >0 Weight increases 1 <0 Weight decreases 0 >0 Weight decreases 0 <0 Weight increases Excel example 27/57

Linear Separability

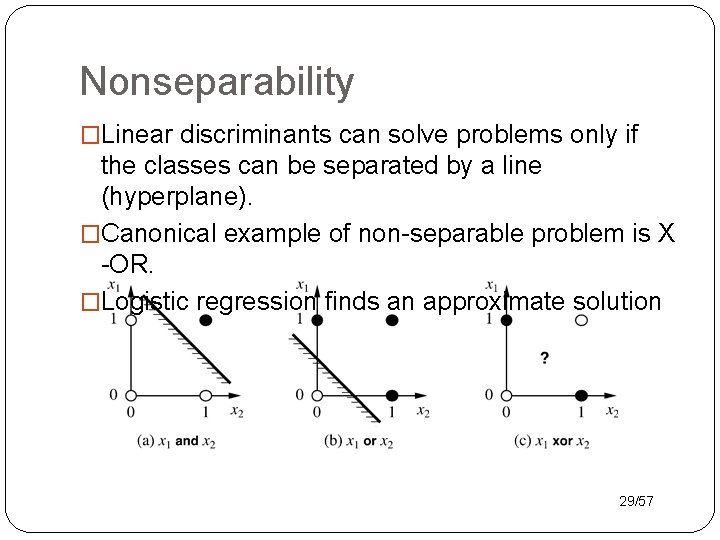
Nonseparability �Linear discriminants can solve problems only if the classes can be separated by a line (hyperplane). �Canonical example of non-separable problem is X -OR. �Logistic regression finds an approximate solution 29/57

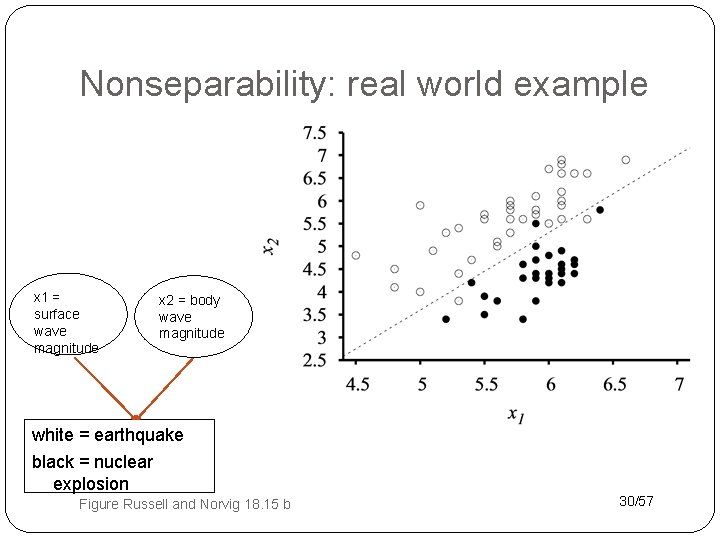
Nonseparability: real world example x 1 = surface wave magnitude x 2 = body wave magnitude white = earthquake black = nuclear explosion Figure Russell and Norvig 18. 15 b 30/57

Logistic Regression With Gaussian Basis Function 3 D version Figure Bishop 4. 12 31/57

Conclusion: Linear Classifiers �Linear Classifiers apply a threshold to a discriminant function to predict class labels �Perfect classification possible only for linearly separable problems �Non-linear basis functions can transform the data so they are linearly separable 32/57

Conclusion: Logistic Regression �If the discriminant function value y represents class log-odds, the logistic function converts y to class probabilities �Logistic regression: assume that class log-odds are a linear function of input features No closed form solution for optimal weight vector. �Can use gradient descent with L 2 loss �Better approaches: �Use likelihood instead of L 2 (see assignment). �Use Iterative Reweighted Least Squares instead of gradient descent. 33/57