CLASSIFICATION CHAPTER 15 Supervised Classification A Dermanis Supervised













- Slides: 20

CLASSIFICATION CHAPTER 15 Supervised Classification A. Dermanis

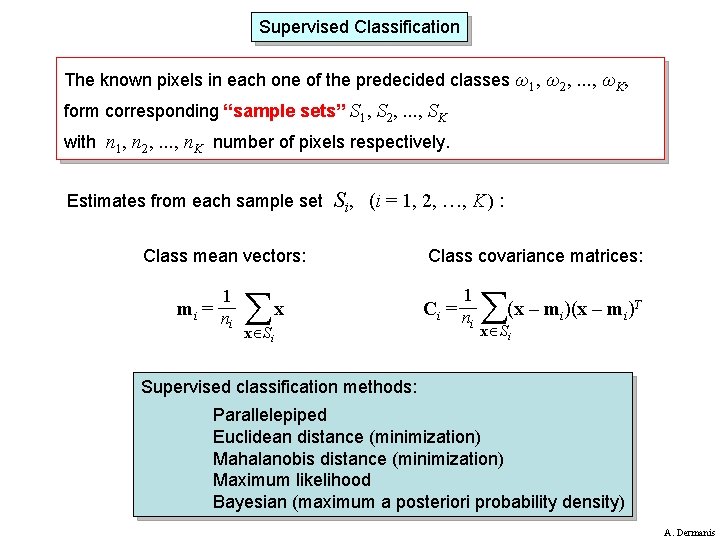
Supervised Classification The known pixels in each one of the predecided classes ω1, ω2, . . . , ωK, form corresponding “sample sets” S 1, S 2, . . . , SK with n 1, n 2, . . . , n. K number of pixels respectively. Estimates from each sample set Si, (i = 1, 2, …, K ) : Class mean vectors: 1 mi = n i x x Si Class covariance matrices: 1 Ci = n i (x – m ) x Si i i T Supervised classification methods: Parallelepiped Euclidean distance (minimization) Mahalanobis distance (minimization) Maximum likelihood Bayesian (maximum a posteriori probability density) A. Dermanis

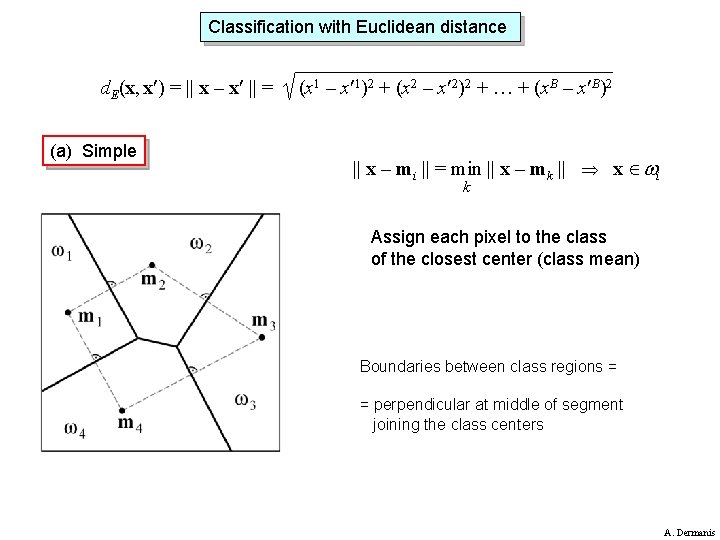
Classification with Euclidean distance d. E(x, x ) = || x – x || = (a) Simple (x 1 – x 1)2 + (x 2 – x 2)2 + … + (x. B – x B)2 || x – mi || = min || x – mk || x i k Assign each pixel to the class of the closest center (class mean) Boundaries between class regions = = perpendicular at middle of segment joining the class centers A. Dermanis

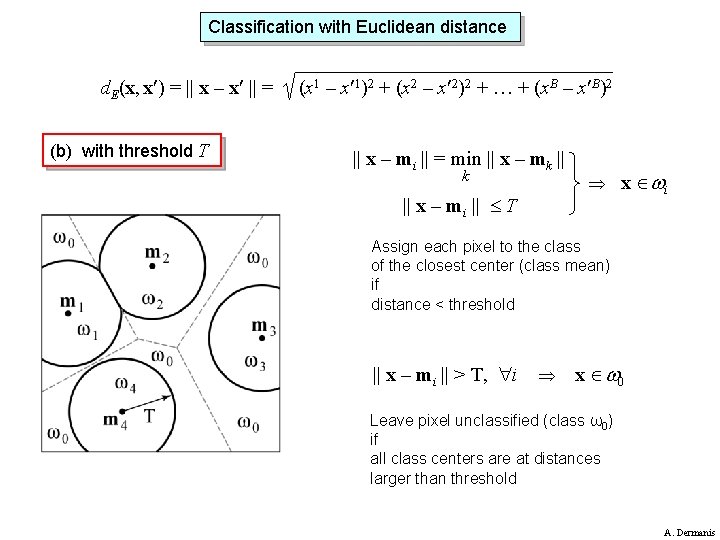
Classification with Euclidean distance d. E(x, x ) = || x – x || = (b) with threshold T (x 1 – x 1)2 + (x 2 – x 2)2 + … + (x. B – x B)2 || x – mi || = min || x – mk || x – mi || T x i Assign each pixel to the class of the closest center (class mean) if distance < threshold || x – mi || > T, i x 0 Leave pixel unclassified (class ω0) if all class centers are at distances larger than threshold A. Dermanis

Classification with Euclidean distance d. E(x, x ) = || x – x || = RIGHT (x 1 – x 1)2 + (x 2 – x 2)2 + … + (x. B – x B)2 WRONG The role of statistics (dispersion) in classification A. Dermanis

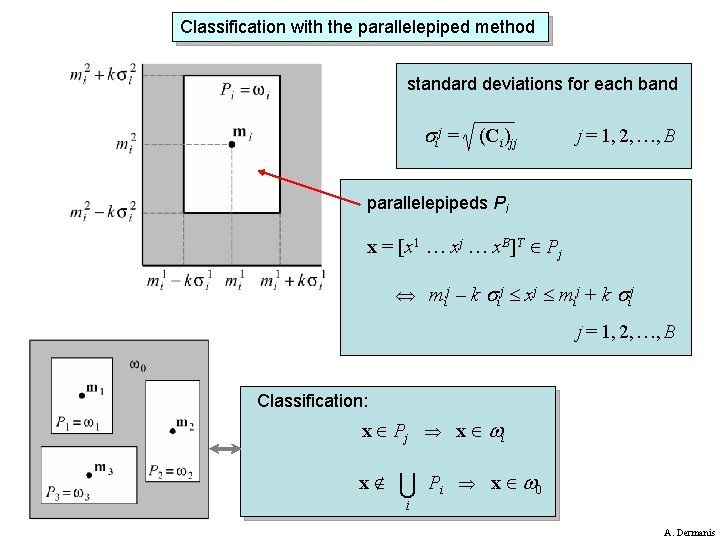
Classification with the parallelepiped method standard deviations for each band ij = (Ci)jj j = 1, 2, …, B parallelepipeds Pi x = [x 1 … xj … x. B]T Pj mij – k ij xj mij + k ij j = 1, 2, …, B Classification: x P j x i x P i x 0 i A. Dermanis

Classification with the Mahalanobis distance: C= 1 N i d. M(x, x ) = (x – mi)T = x Si Classification (simple): Classification with threshold: (x – x )T C– 1 (x – x ) 1 N n. C i i (total covariance matrix) i d. M(x, mi) < d. M(x, mk), k i d. M(x, mi) T, x i d. M(x, mi) > T, i x 0 A. Dermanis

Classification with the maximum likelihood method Probability distribution density function or likelihood function of class ωi: li(x) = 1 (2 )B/2 | Ci |1/2 Classification: exp [ – 1 (x – mi)T Ci– 1 (x – mi) ] 2 li(x) > lk(x) k i x i Equivalent use of decision function: di(x) = 2 ln[li(x)] + B ln(2 ) = – ln | Ci | – (x – mi)T Ci– 1 (x – mi) di(x) > dk(x) k i x i A. Dermanis

Classification using the Bayesian approach N: total number of pixels in the image (i. e. in each band) B: number of bands, ω1, ω2, …, ωK : the K classes present in the image Ni : number of image pixels belonging to the class ωi (i = 1, 2, …, K) nx : number of pixels with value x (= vector of values in all bands) nxi : number of pixels with value x which also belong to the class ωi A. Dermanis

Classification using the Bayesian approach N: total number of pixels in the image (i. e. in each band) B: number of bands, ω1, ω2, …, ωK : the K classes present in the image Ni : number of image pixels belonging to the class ωi (i = 1, 2, …, K) nx : number of pixels with value x (= vector of values in all bands) nxi : number of pixels with value x which also belong to the class ωi A. Dermanis

Classification using the Bayesian approach N: total number of pixels in the image (i. e. in each band) B: number of bands, ω1, ω2, …, ωK : the K classes present in the image Ni : number of image pixels belonging to the class ωi (i = 1, 2, …, K) nx : number of pixels with value x (= vector of values in all bands) nxi : number of pixels with value x which also belong to the class ωi Basic identity: A. Dermanis

Classification using the Bayesian approach N: total number of pixels in the image (i. e. in each band) B: number of bands, ω1, ω2, …, ωK : the K classes present in the image Ni : number of image pixels belonging to the class ωi (i = 1, 2, …, K) nx : number of pixels with value x (= vector of values in all bands) nxi : number of pixels with value x which also belong to the class ωi Basic identity: A. Dermanis

Classification using the Bayesian approach N: total number of pixels in the image (i. e. in each band) B: number of bands, ω1, ω2, …, ωK : the K classes present in the image Ni : number of image pixels belonging to the class ωi (i = 1, 2, …, K) nx : number of pixels with value x (= vector of values in all bands) nxi : number of pixels with value x which also belong to the class ωi Basic identity: A. Dermanis

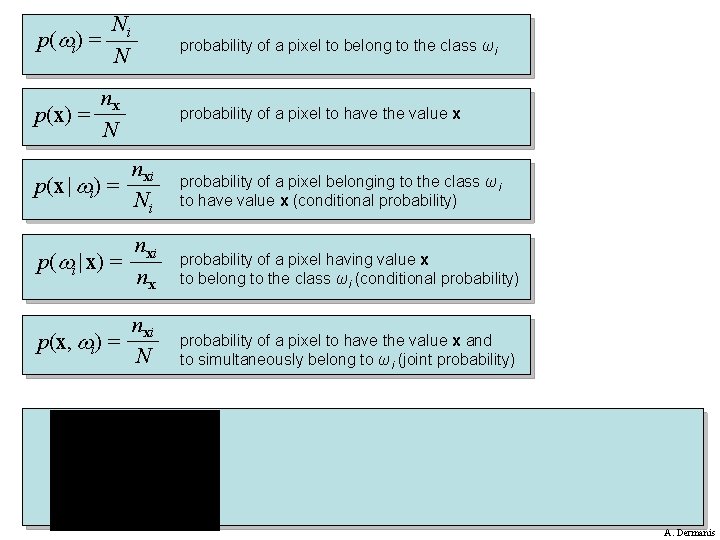
Ni p( i) = N probability of a pixel to belong to the class ωi nx p(x) = N probability of a pixel to have the value x nxi p(x | i) = Ni probability of a pixel belonging to the class ωi to have value x (conditional probability) nxi p( i | x) = nx probability of a pixel having value x to belong to the class ωi (conditional probability) nxi p(x, i) = N probability of a pixel to have the value x and to simultaneously belong to ωi (joint probability) A. Dermanis

Ni p( i) = N probability of a pixel to belong to the class ωi nx p(x) = N probability of a pixel to have the value x nxi p(x | i) = Ni probability of a pixel belonging to the class ωi to have value x (conditional probability) nxi p( i | x) = nx probability of a pixel having value x to belong to the class ωi (conditional probability) nxi p(x, i) = N probability of a pixel to have the value x and to simultaneously belong to ωi (joint probability) A. Dermanis

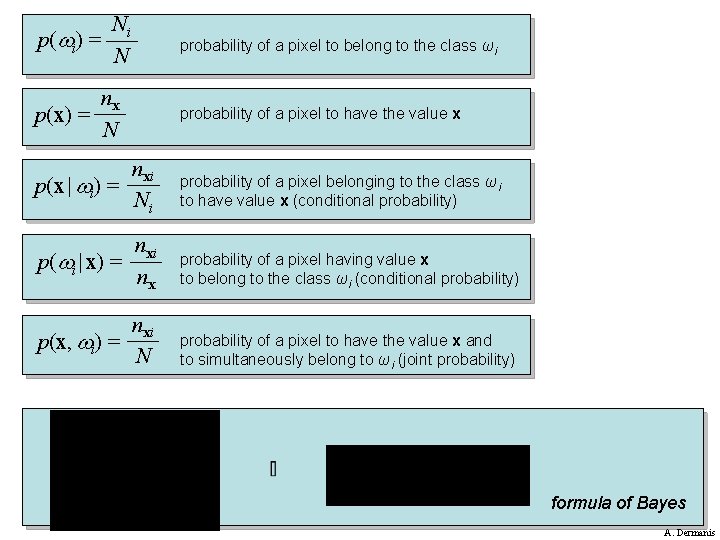
Ni p( i) = N probability of a pixel to belong to the class ωi nx p(x) = N probability of a pixel to have the value x nxi p(x | i) = Ni probability of a pixel belonging to the class ωi to have value x (conditional probability) nxi p( i | x) = nx probability of a pixel having value x to belong to the class ωi (conditional probability) nxi p(x, i) = N probability of a pixel to have the value x and to simultaneously belong to ωi (joint probability) formula of Bayes A. Dermanis

The Bayes theorem: Pr(A B) Pr(A | B) = Pr(B) Pr(A | B) Pr(B) = Pr(A B) = Pr(B | A) Pr(A | B) Pr(B | A) = Pr(A) event A = occurrence of the value x event B = occurence of the class ωi p(x| i) p( i|x) = p(x) Classification: p( i |x) > p( k |x) k i x i p(x) = not necessary (common constant factor) Classification: p(x | i) p( i) > p(x | k) p( k) k i A. Dermanis

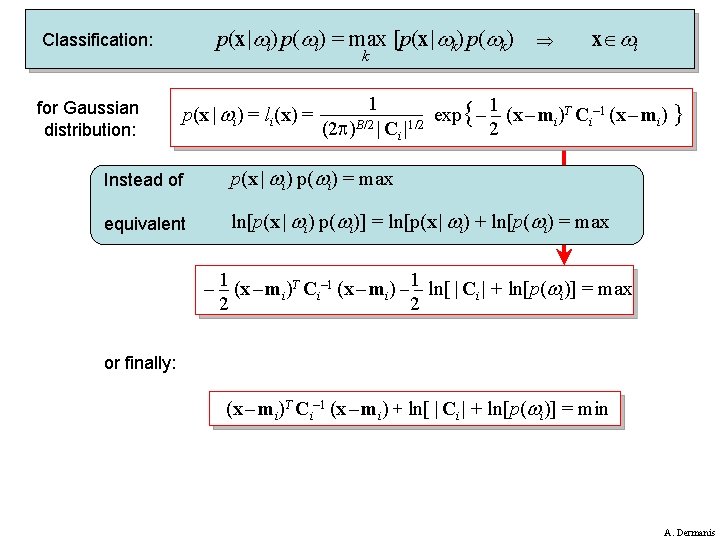
p(x| i) p( i) = max [p(x| k) p( k) Classification: for Gaussian distribution: k p(x | i) = li(x) = x i 1 1 T C – 1 (x – m ) } exp { – – (x – m ) i i i (2 )B/2 | Ci |1/2 2 Instead of p(x | i) p( i) = max equivalent ln[p(x | i) p( i)] = ln[p(x | i) + ln[p( i) = max – – 1 (x – mi)T Ci– 1 (x – mi) – 1– ln[ | Ci | + ln[p( i)] = max 2 2 or finally: (x – mi)T Ci– 1 (x – mi) + ln[ | Ci | + ln[p( i)] = min A. Dermanis

Bayesian Classification for Gaussian distribution : (x – mi)T Ci– 1 (x – mi) + ln[ | Ci | + ln[p( i)] = min SPECIAL CASES: p( 1) = p( 2) = … = p( K) (x – mi)T Ci– 1 (x – mi) + ln[ | Ci | = min Maximum Likelihood ! p( 1) = p( 2) = … = p( K) C 1 = C 2 = … = CK = C (x – mi)T Ci– 1 (x – mi) = min Mahalanobis distance ! p( 1) = p( 2) = … = p( K) C 1 = C 2 = … = CK = I (x – mi)T (x – mi) = min Euclidean distance ! A. Dermanis

Want to learn more ? A. Dermanis L. Biagi: Telerilevamento Casa Editrice Ambrosiana