CLASSIFICATION CHAPTER 13 Pattern Recognition and Classification A

Pattern Recognition: Identification of a particular object within a class of similar objects by

Decision functions A decision function for each class ω1, ω2, …, ωΚ : di(x)

Examples of boundaries for linear decision functions d(x) = w. T x + w

Classification by distance functions Replace di(x) = max with ρi(x) = ρi(mi, x) =

Classification by distance functions Euclidean distance function : (mi, x) = || x –

Non-linear decision functions Example of non-linear decision functions: 2 classes, 1 band Example of

Slides: 7

Download presentation

CLASSIFICATION CHAPTER 13 Pattern Recognition and Classification A. Dermanis

Pattern Recognition: Identification of a particular object within a class of similar objects by exploitation of object-related measurements and a-priori information (patterns) on all class elements Pattern Recognition = A collection of mathematical-statistical tools and algorithms independent from particular applications Examples of pattern recognition applications: Recognition of letters (scanning of texts – artificial reading) Speech recognition (artificial hearing) Voice recognition (identification of a person by his speech) Medical diagnosis (identification of decease) Classification of image pixels (Remote Sensing) A. Dermanis

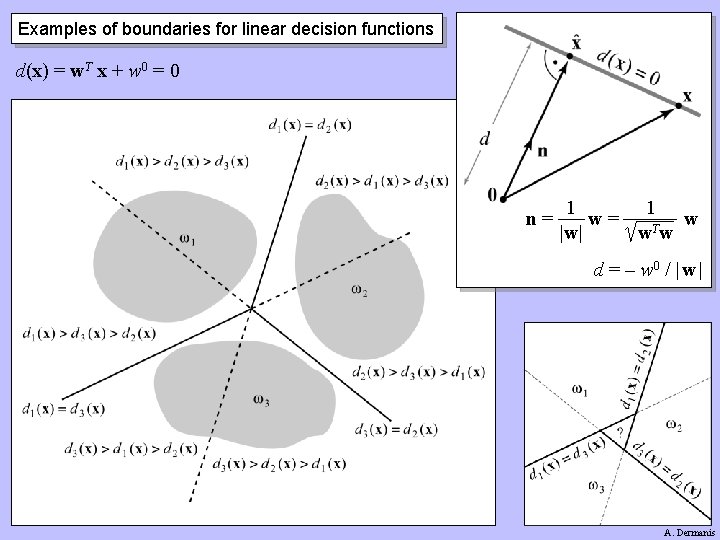
Decision functions A decision function for each class ω1, ω2, …, ωΚ : di(x) = di(x 1, x 2, …, x. B) Assign each pixel to the class with maximum value of decision function : x j: dj(x) > dk(x), k j Spectral space separated into class regions with boundaries : dj(x) = dk(x) Linear decision functions di(x) = wi 1 x 1 + wi 2 x 2 + … + wi. B x. B + wi 0 = wi. T x + wi 0 Boundary between any 2 classes ωi and ωj : dij(x) di(x) – dj(x) = wi. T x + wi 0 – wj. T x – wj 0 = (wi. T – wj. T) x + (wi 0 – wj 0) wij. T x + wij 0 = 0 simplified to : w. T x + w 0 = 0 A. Dermanis

Examples of boundaries for linear decision functions d(x) = w. T x + w 0 = 0 n= 1 1 w= w |w| w. T w d = – w 0 / | w | A. Dermanis

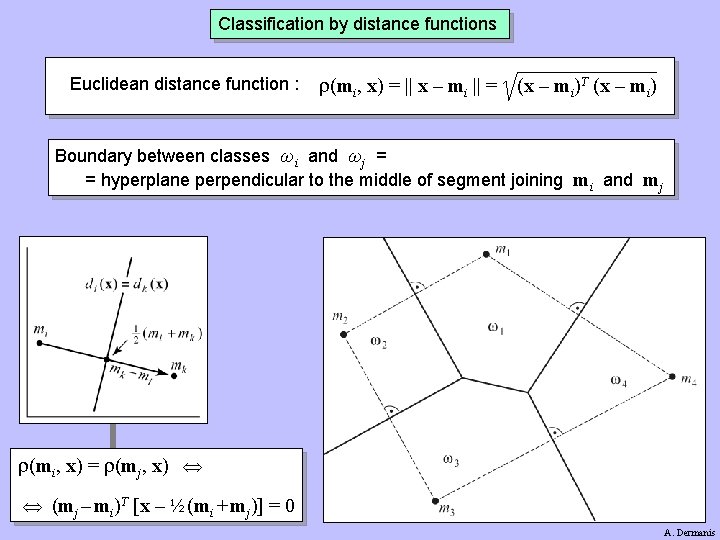
Classification by distance functions Replace di(x) = max with ρi(x) = ρi(mi, x) = min : di(x ) > di(x) i(x ) > i(x) mi = center of class ωi (usually mean of sample of class pixels) Assign each pixel to the class with minimum value of distance function : x j: j(x) > k(x), k j Decision functions derived from distance functions : di(x) = C – i(x), di(x) = C – [ i(x)]2, di(x) = C / i(x) A. Dermanis

Classification by distance functions Euclidean distance function : (mi, x) = || x – mi || = (x – mi)T (x – mi) Boundary between classes ωi and ωj = = hyperplane perpendicular to the middle of segment joining mi and mj (mi, x) = (mj, x) (mj – mi)T [x – ½ (mi + mj)] = 0 A. Dermanis

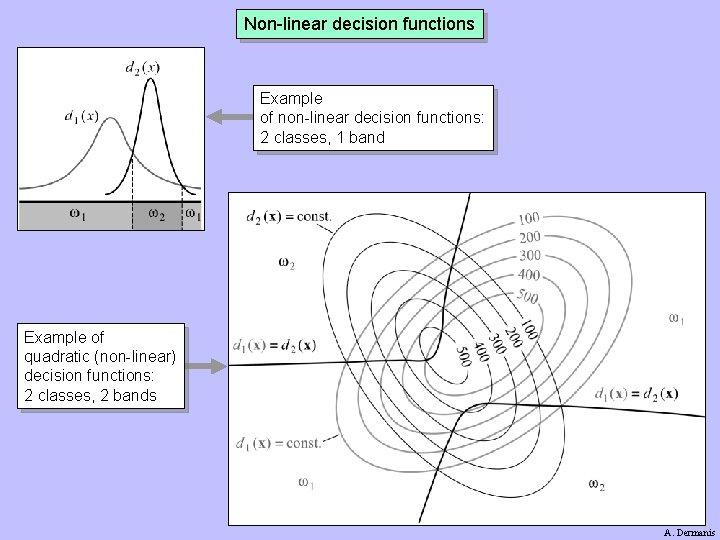
Non-linear decision functions Example of non-linear decision functions: 2 classes, 1 band Example of quadratic (non-linear) decision functions: 2 classes, 2 bands A. Dermanis