Classification Algorithms Decision Tree Algorithms The problem Given

Classification Algorithms Decision Tree Algorithms

The problem • Given a set of training cases/objects and their attribute values, try to determine the target attribute value of new cases. – Classification – Prediction

Why decision tree? • Decision trees are powerful and popular tools for classification and prediction. • Decision trees represent rules, which can be understood by humans and used in knowledge system such as database.

key requirements • Attribute-value description: object or case must be expressible in terms of a fixed collection of properties or attributes (e. g. , hot, mild, cold). • Predefined classes (target values): the target function has discrete output values (Boolean or multiclass) • Sufficient data: enough training cases should be provided to learn the model.

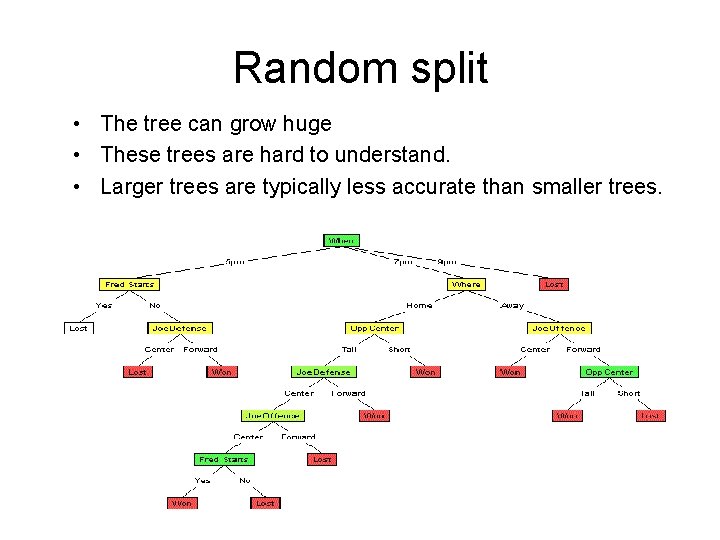
Random split • The tree can grow huge • These trees are hard to understand. • Larger trees are typically less accurate than smaller trees.

Principled Criterion • Selection of an attribute to test at each node - choosing the most useful attribute for classifying examples. • information gain – measures how well a given attribute separates the training examples according to their target classes – This measure is used to select among the candidate attributes at each step while growing the tree

Entropy • A measure of homogeneity of the set of examples. • Given a set S of positive and negative examples of some target concept (a 2 -class problem), the entropy of set S relative to this binary classification is E(S) = - p 1*log 2 p 1 – p 2*log 2 p 2

Example • Suppose S has 25 examples, 15 positive and 10 negatives [15+, 10 -]. Then the entropy of S relative to this classification is E(S)=-(15/25) log 2(15/25) - (10/25) log 2 (10/25)

Entropy • Entropy is minimized when all values of the target attribute are the same. – If we know that Joe always plays Center Offence, then entropy of Offence is 0 • Entropy is maximized when there is an equal chance of all values for the target attribute (i. e. the result is random) – If offence = center in 9 instances and forward in 9 instances, entropy is maximized

Information Gain • Information gain measures the expected reduction in entropy, or uncertainty. – Values(A) is the set of all possible values for attribute A, and Sv the subset of S for which attribute A has value v Sv = {s in S | A(s) = v}. – the first term in the equation for Gain is just the entropy of the original collection S – the second term is the expected value of the entropy after S is partitioned using attribute A

Information Gain • It is simply the expected reduction in entropy caused by partitioning the examples according to this attribute. • It is the number of bits saved when encoding the target value of an arbitrary member of S, by knowing the value of attribute A.

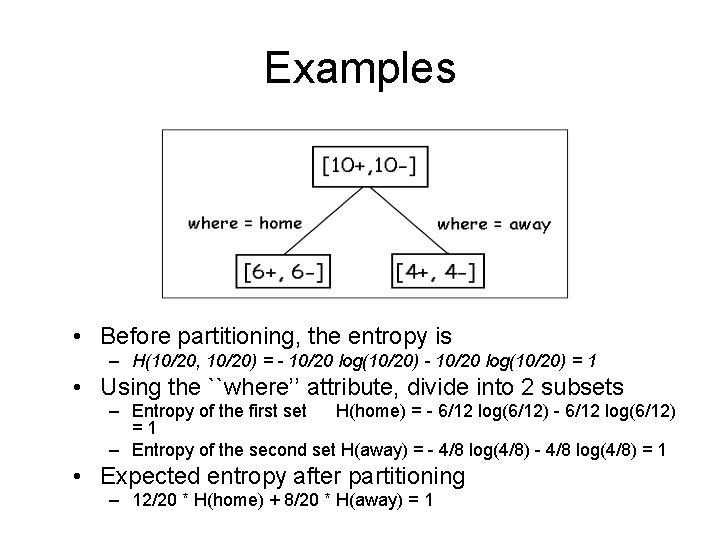
Examples • Before partitioning, the entropy is – H(10/20, 10/20) = - 10/20 log(10/20) = 1 • Using the ``where’’ attribute, divide into 2 subsets – Entropy of the first set H(home) = - 6/12 log(6/12) = 1 – Entropy of the second set H(away) = - 4/8 log(4/8) = 1 • Expected entropy after partitioning – 12/20 * H(home) + 8/20 * H(away) = 1

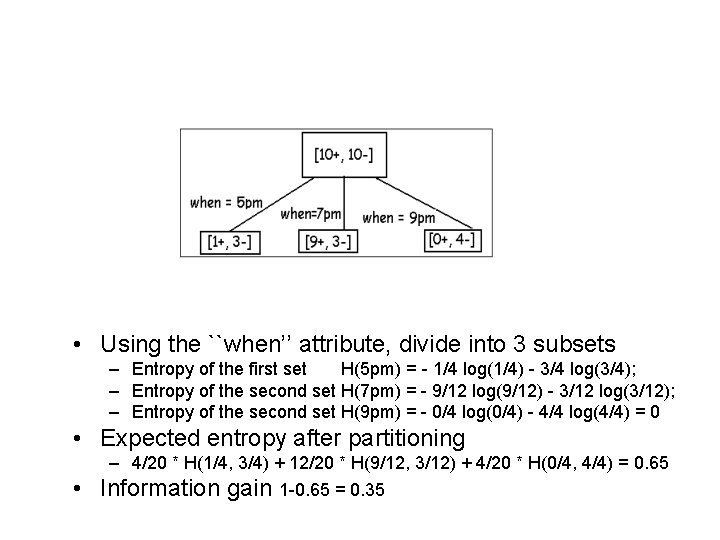
• Using the ``when’’ attribute, divide into 3 subsets – Entropy of the first set H(5 pm) = - 1/4 log(1/4) - 3/4 log(3/4); – Entropy of the second set H(7 pm) = - 9/12 log(9/12) - 3/12 log(3/12); – Entropy of the second set H(9 pm) = - 0/4 log(0/4) - 4/4 log(4/4) = 0 • Expected entropy after partitioning • – 4/20 * H(1/4, 3/4) + 12/20 * H(9/12, 3/12) + 4/20 * H(0/4, 4/4) = 0. 65 Information gain 1 -0. 65 = 0. 35

Decision • Knowing the ``when’’ attribute values provides larger information gain than ``where’’. • Therefore the ``when’’ attribute should be chosen for testing prior to the ``where’’ attribute. • Similarly, we can compute the information gain for other attributes. • At each node, choose the attribute with the largest information gain.

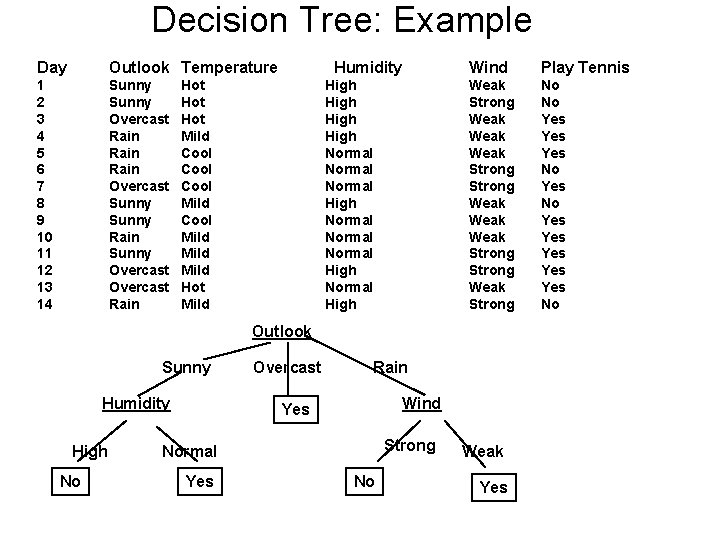
Decision Tree: Example Day Outlook Temperature 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Sunny Overcast Rain Overcast Sunny Rain Sunny Overcast Rain Humidity Hot Hot Mild Cool Mild Hot Mild High Normal Normal High Wind Play Tennis Weak Strong Weak Weak Strong Weak Strong No No Yes Yes Yes No Outlook Sunny Humidity High No Overcast Rain Wind Yes Strong Normal Yes No Weak Yes

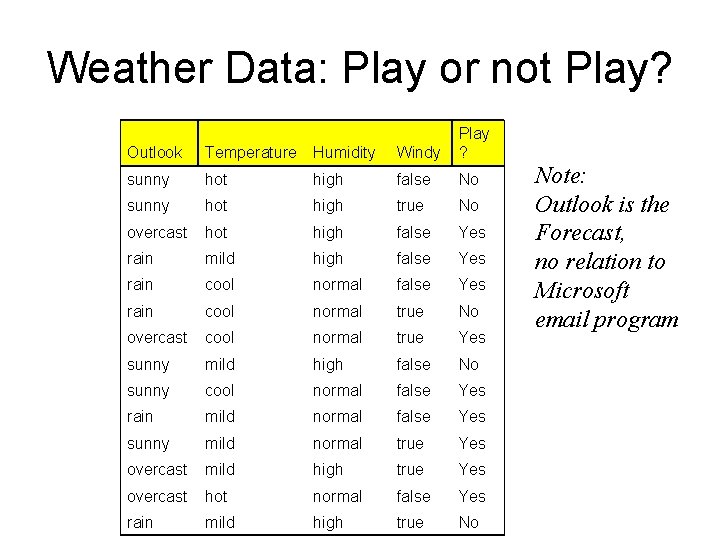
Weather Data: Play or not Play? Outlook Temperature Humidity Windy Play ? sunny hot high false No sunny hot high true No overcast hot high false Yes rain mild high false Yes rain cool normal true No overcast cool normal true Yes sunny mild high false No sunny cool normal false Yes rain mild normal false Yes sunny mild normal true Yes overcast mild high true Yes overcast hot normal false Yes rain mild high true No Note: Outlook is the Forecast, no relation to Microsoft email program

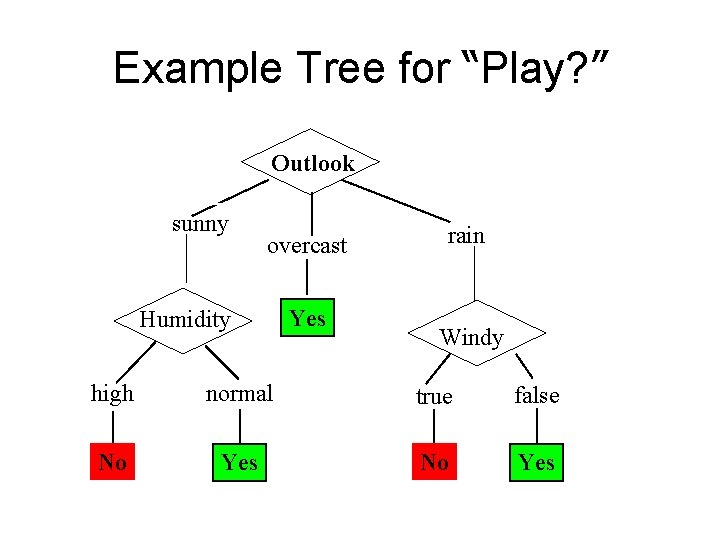
Example Tree for “Play? ” Outlook sunny overcast Humidity Yes rain Windy high normal true false No Yes

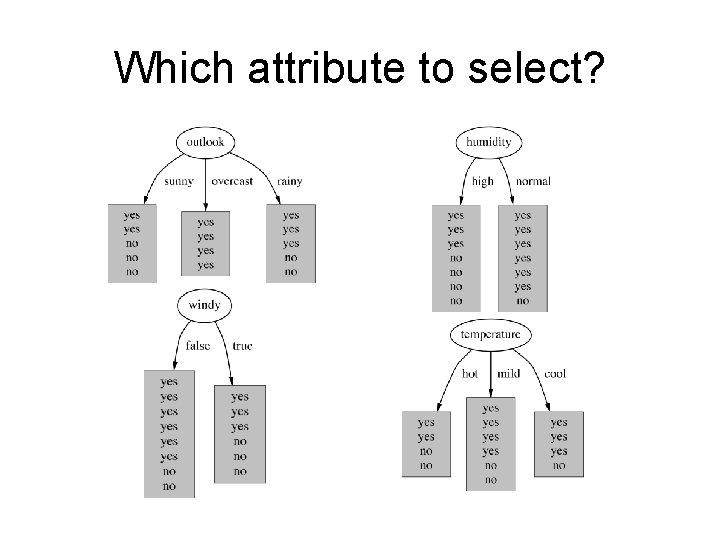
Which attribute to select?

Example: attribute “Outlook” • “Outlook” = “Sunny”: • “Outlook” = “Overcast”: • “Outlook” = “Rainy”: Note: log(0) is not defined, but we evaluate 0*log(0) as zero • Expected information for attribute:

Computing the information gain • Information gain: (information before split) – (information after split) • Information gain for attributes from weather data:

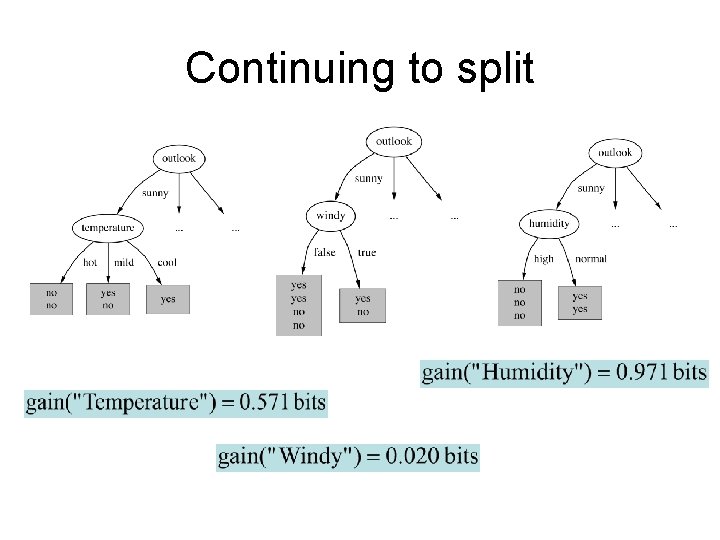
Continuing to split

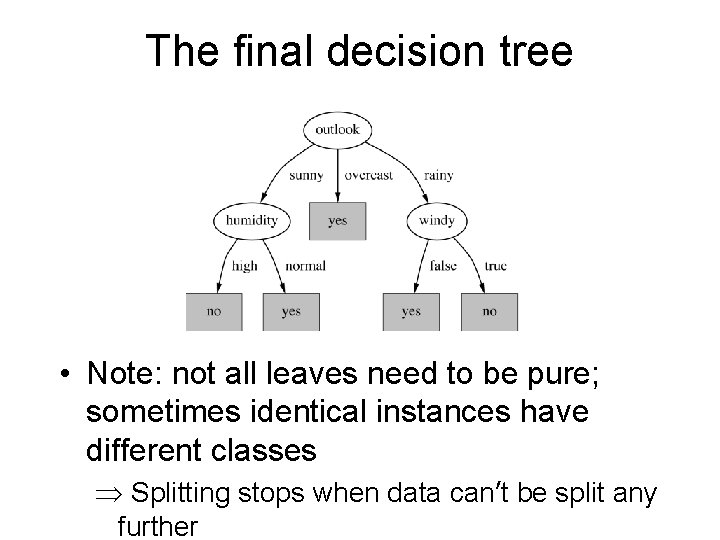
The final decision tree • Note: not all leaves need to be pure; sometimes identical instances have different classes Splitting stops when data can’t be split any further

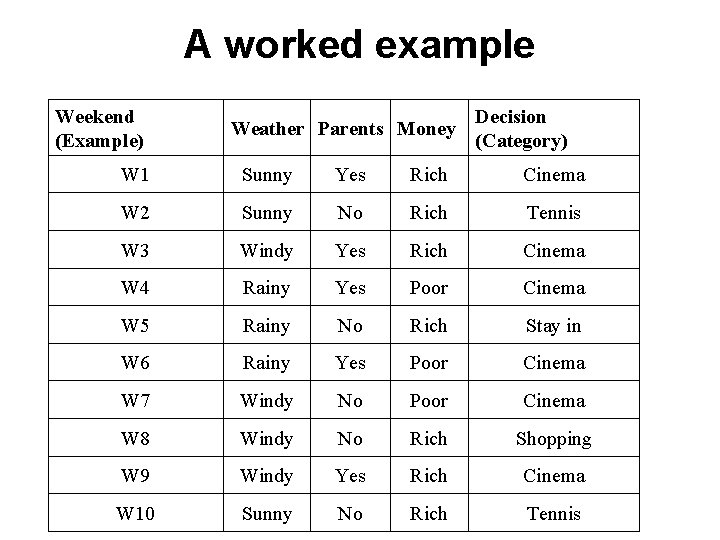
A worked example Weekend (Example) Weather Parents Money Decision (Category) W 1 Sunny Yes Rich Cinema W 2 Sunny No Rich Tennis W 3 Windy Yes Rich Cinema W 4 Rainy Yes Poor Cinema W 5 Rainy No Rich Stay in W 6 Rainy Yes Poor Cinema W 7 Windy No Poor Cinema W 8 Windy No Rich Shopping W 9 Windy Yes Rich Cinema W 10 Sunny No Rich Tennis

Determining the Best Attribute Entropy(S) = -pcinema log 2(pcinema) -ptennis log 2(ptennis) – pshopping log 2(pshopping) –pstay_in log 2(pstay_in) = -(6/10) * log 2(6/10) -(2/10) * log 2(2/10) -(1/10) * log 2(1/10) = -(6/10) * -0. 737 -(2/10) * -2. 322 -(1/10) * -3. 322 = 0. 4422 + 0. 4644 + 0. 3322 = 1. 571 and we need to determine the best of: Gain(S, weather) = 1. 571 - (|Ssun|/10)*Entropy(Ssun) – (|Swind|/10)*Entropy(Swind) – (|Srain|/10)*Entropy(Srain) = 1. 571 - (0. 3)*Entropy(Ssun) - (0. 4)*Entropy(Swind) – (0. 3)*Entropy(Srain) = 1. 571 - (0. 3)*(0. 918) - (0. 4)*(0. 81125) - (0. 3)*(0. 918) = 0. 70 Gain(S, parents) = 1. 571 - (|Syes|/10)*Entropy(Syes) - (|Sno|/10)*Entropy(Sno) = 1. 571 - (0. 5) * 0 - (0. 5) * 1. 922 = 1. 571 - 0. 961 = 0. 61 Gain(S, money) = 1. 571 - (|Srich|/10)*Entropy(Srich) - (|Spoor|/10)*Entropy(Spoor) = 1. 571 - (0. 7) * (1. 842) - (0. 3) * 0 = 1. 571 - 1. 2894 = 0. 2816

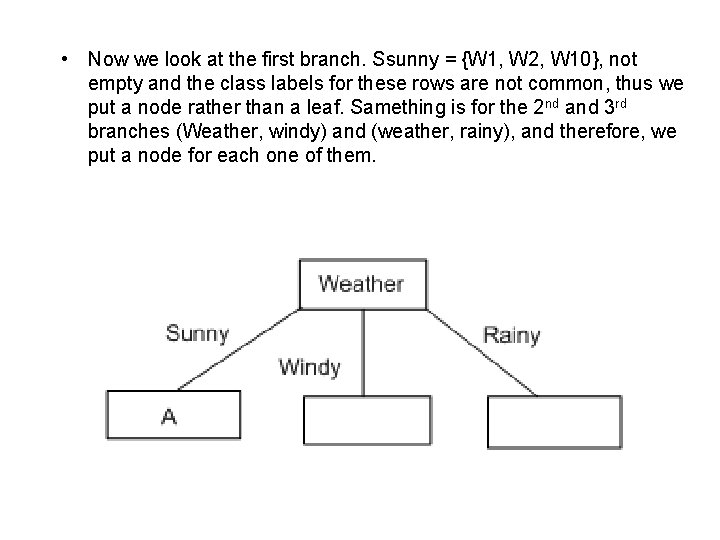
• Now we look at the first branch. Ssunny = {W 1, W 2, W 10}, not empty and the class labels for these rows are not common, thus we put a node rather than a leaf. Samething is for the 2 nd and 3 rd branches (Weather, windy) and (weather, rainy), and therefore, we put a node for each one of them.

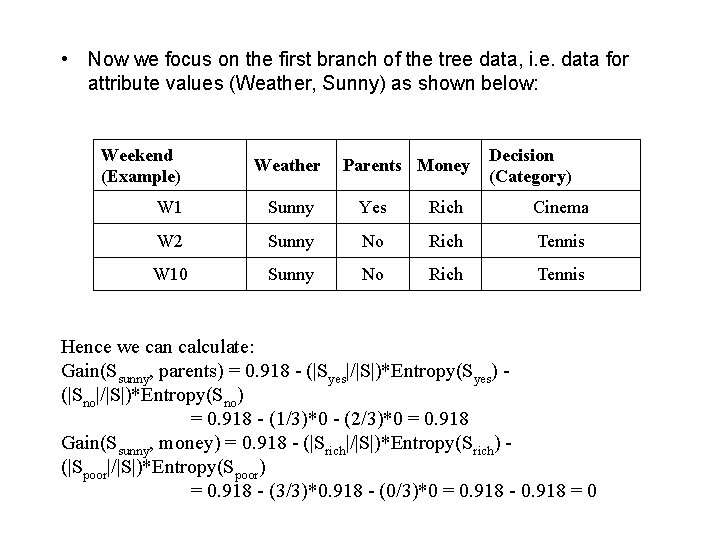
• Now we focus on the first branch of the tree data, i. e. data for attribute values (Weather, Sunny) as shown below: Weekend (Example) Weather Parents Money Decision (Category) W 1 Sunny Yes Rich Cinema W 2 Sunny No Rich Tennis W 10 Sunny No Rich Tennis Hence we can calculate: Gain(Ssunny, parents) = 0. 918 - (|Syes|/|S|)*Entropy(Syes) - (|Sno|/|S|)*Entropy(Sno) = 0. 918 - (1/3)*0 - (2/3)*0 = 0. 918 Gain(Ssunny, money) = 0. 918 - (|Srich|/|S|)*Entropy(Srich) - (|Spoor|/|S|)*Entropy(Spoor) = 0. 918 - (3/3)*0. 918 - (0/3)*0 = 0. 918 - 0. 918 = 0

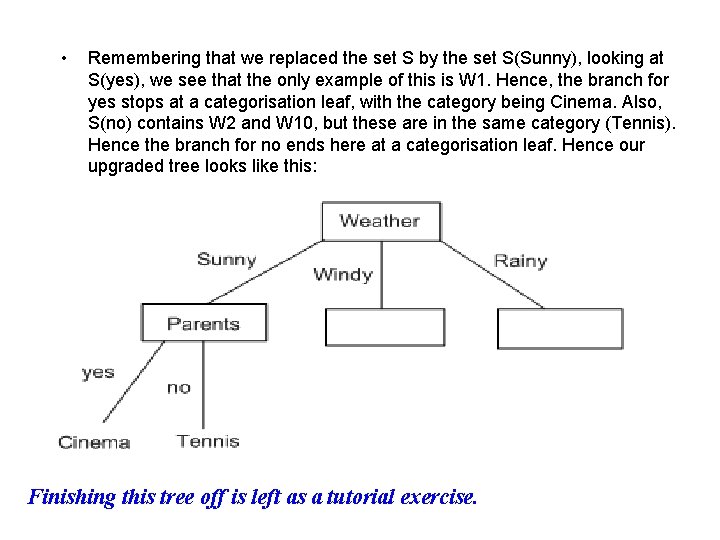
• Remembering that we replaced the set S by the set S(Sunny), looking at S(yes), we see that the only example of this is W 1. Hence, the branch for yes stops at a categorisation leaf, with the category being Cinema. Also, S(no) contains W 2 and W 10, but these are in the same category (Tennis). Hence the branch for no ends here at a categorisation leaf. Hence our upgraded tree looks like this: Finishing this tree off is left as a tutorial exercise.