Classification 1 Classification Task Given a set of

§Classification 1

Classification § Task: Given a set of pre-classified examples, build a model or classifier to classify new cases. § Supervised learning: classes are known for the examples used to build the classifier. § A classifier can be a set of rules, a decision tree, a neural network, etc. § Typical applications: credit approval, direct marketing, fraud detection, medical diagnosis, …. . 2

Simplicity first § Simple algorithms often work very well! § There are many kinds of simple structure, eg: § § One attribute does all the work § All attributes contribute equally & independently § A weighted linear combination might do § Instance-based: use a few prototypes § Use simple logical rules Success of method depends on the domain 3

Inferring rudimentary rules § 1 R: learns a 1 -level decision tree § § I. e. , rules that all test one particular attribute Basic version § One branch for each value § Each branch assigns most frequent class § Error rate: proportion of instances that don’t belong to the majority class of their corresponding branch § Choose attribute with lowest error rate (assumes nominal attributes) 4

Pseudo-code for 1 R For each attribute, For each value of the attribute, make a rule as follows: count how often each class appears find the most frequent class make the rule assign that class to this attribute-value Calculate the error rate of the rules Choose the rules with the smallest error rate § Note: “missing” is treated as a separate attribute value 5

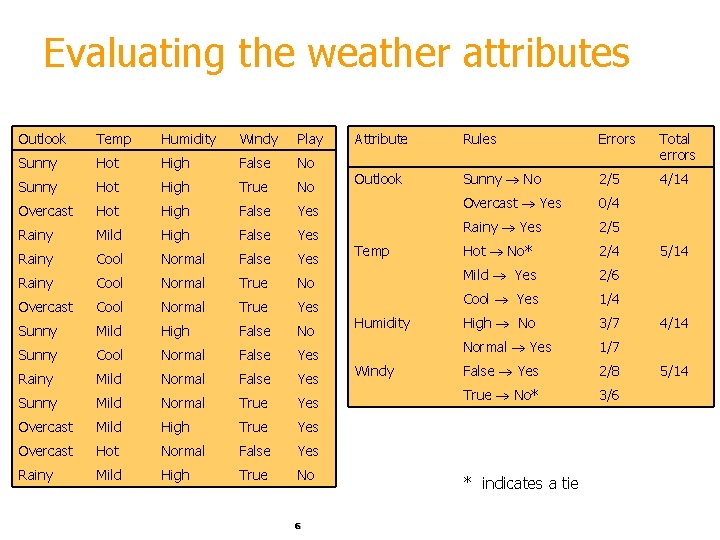
Evaluating the weather attributes Outlook Temp Humidity Windy Play Sunny Hot High False No Sunny Hot High True No Overcast Hot High False Yes Rainy Mild High False Yes Rainy Cool Normal True No Overcast Cool Normal True Yes Sunny Mild High False No Sunny Cool Normal False Yes Rainy Mild Normal False Yes Sunny Mild Normal True Yes Overcast Mild High True Yes Overcast Hot Normal False Yes Rainy Mild High True No 6 Attribute Rules Errors Total errors Outlook Sunny No 2/5 4/14 Overcast Yes 0/4 Rainy Yes 2/5 Hot No* 2/4 Mild Yes 2/6 Cool Yes 1/4 High No 3/7 Normal Yes 1/7 False Yes 2/8 True No* 3/6 Temp Humidity Windy * indicates a tie 5/14 4/14 5/14

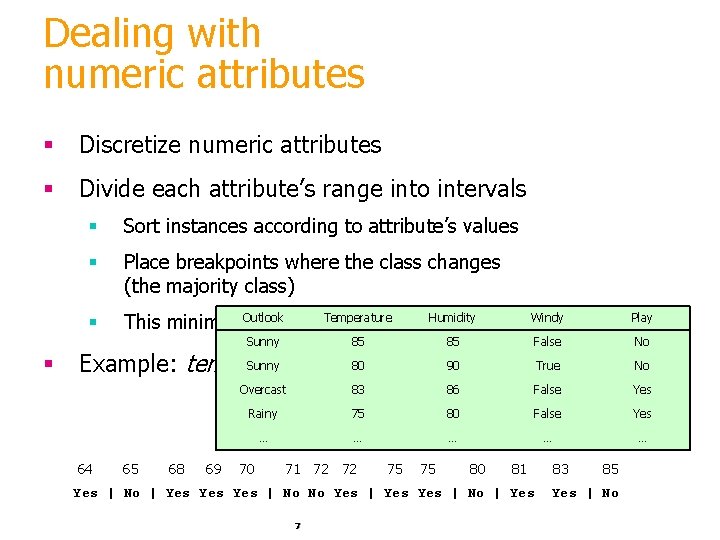
Dealing with numeric attributes § Discretize numeric attributes § Divide each attribute’s range into intervals § § Sort instances according to attribute’s values § Place breakpoints where the class changes (the majority class) § Outlook This minimizes the total. Temperature error Sunny Humidity Windy Play 85 False No True No 85 Sunny 80 weather 90 data Example: temperature from 64 65 68 69 Overcast 83 86 False Yes Rainy 75 80 False Yes … … … 70 71 72 72 75 75 80 81 Yes | No | Yes Yes | No No Yes | No | Yes 7 83 85 Yes | No

The problem of overfitting § This procedure is very sensitive to noise § One instance with an incorrect class label will probably produce a separate interval § Also: time stamp attribute will have zero errors § Simple solution: enforce minimum number of instances in majority class per interval 8

Discretization example Example (with min = 3): § 64 65 68 69 70 71 72 72 75 75 80 81 Yes | No | Yes Yes | No No Yes | No | Yes 83 85 Yes | No Final result for temperature attribute § 64 65 68 69 70 71 72 72 Yes No Yes Yes | No No Yes 9 75 75 80 Yes | No 81 83 85 Yes No

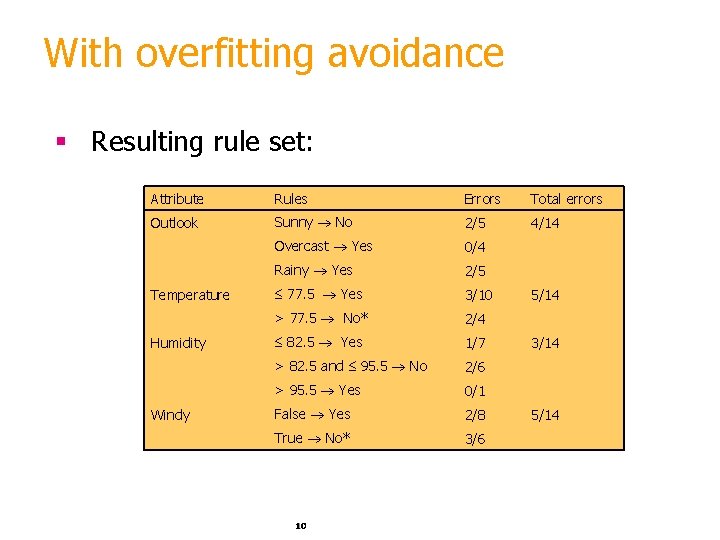
With overfitting avoidance § Resulting rule set: Attribute Rules Errors Total errors Outlook Sunny No 2/5 4/14 Overcast Yes 0/4 Rainy Yes 2/5 77. 5 Yes 3/10 > 77. 5 No* 2/4 82. 5 Yes 1/7 > 82. 5 and 95. 5 No 2/6 > 95. 5 Yes 0/1 False Yes 2/8 True No* 3/6 Temperature Humidity Windy 10 5/14 3/14 5/14

§Missing Values 11

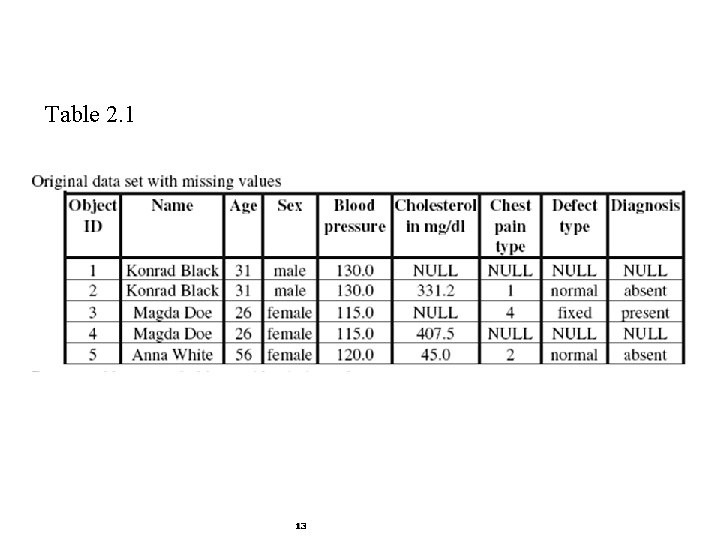
Missing Values Many data sets are plagued by the problem of missing values § missing values can be a result of manual data entry, incorrect measurements, equipment errors, etc. § they are usually denoted by special characters such as: NULL * 12

Table 2. 1 13

Missing Values § imputation (filling-in) of missing data We will use two ways of single imputation: § Single Imputation § Hot Deck Imputation 14

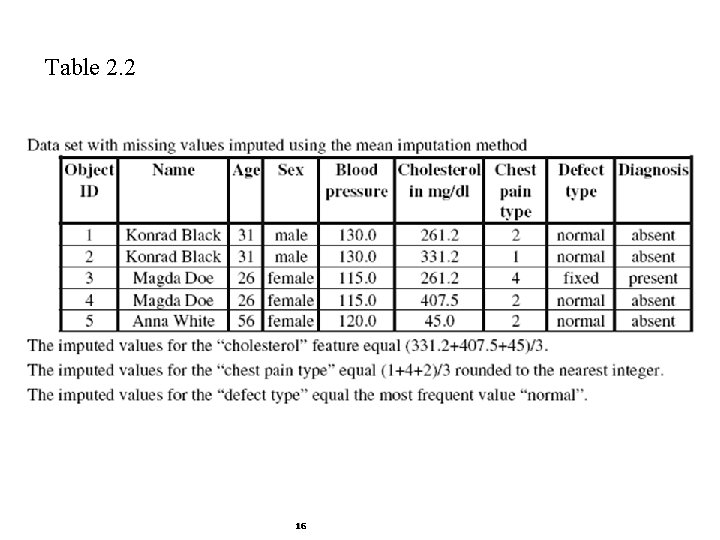
Missing Values § single imputation § mean imputation method uses the mean of values of a feature that contains missing data § in case of a symbolic/categorical feature, a mode (the most frequent value) is used § the algorithm imputes missing values for each attribute separately 15

Table 2. 2 16

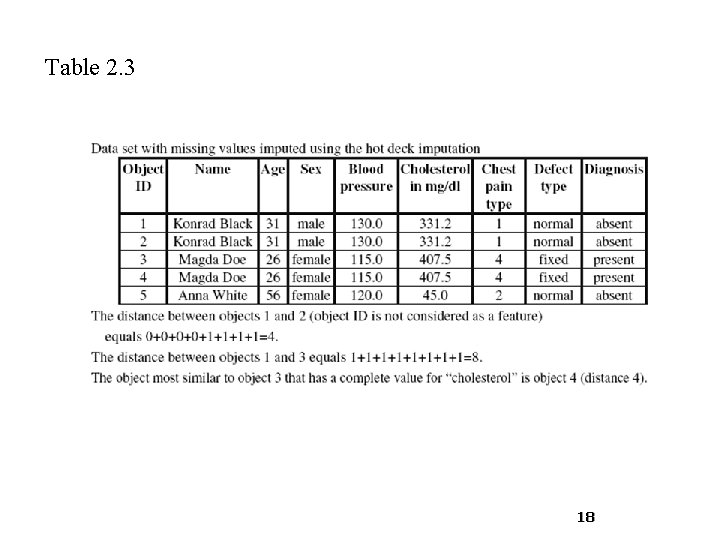
Missing Values - single imputation § hot deck imputation: for each object that contains missing values the most similar object (according to some distance function) is found, and the missing values are imputed from that object § if the most similar record also contains missing values for the same feature then it is discarded another closest object is found § the procedure is repeated until all the missing values are imputed § when no similar object is found, the closest object with the minimum number of missing values is chosen to impute the missing values 17

Table 2. 3 18

Noise 19

Noise Def. : Noise in the data is defined as a value that is a random error or variance in a measured feature § the amount of noise in the data can jeopardize the entire KDP results § the influence of noise on the data can be prevented by imposing constraints on features to detect anomalies when the data is entered § for instance, DBMS usually provides facility to define constrains for individual attributes 20

Noise Detection § In manual inspection, the user checks feature values against predefined constraints and manually detects the noise § For example, for object 5 in table 2. 3 , the cholesterol value is 45. 0, which is outside the predefined acceptable interval for this feature, namely, within [50. 0, 600. 0]. 21

Noise can be removed using § Binning § Requires ordering values of the noisy feature and then substituting the values with a mean or median value for predefined bins § In table 2. 3, the attribute of Cholesterol contains the value of “ 45” which is a noise. Binning first orders the values of the noisy feature and then replaces the values with a mean or median value for the predefined bins. As an example, let us consider the cholesterol feature, with its values 45. 0, 261. 2, 331. 2, and 407. 5. If the bin size equals two, two bins are created: bin 1 with 45. 0 and 261. 2, and bin 2 with 331. 2 and 407. 5. For bin 1 the mean value is 153. 1, and for bin 2 it is 369. 4. Therefore the values 45. 0 and 261. 2 would be replaced with 153. 1 and the values 331. 2 and 407. 5 with 369. 4. Note that the two new values are within the acceptable interval. 22