CLASSICAL RELATIONS AND FUZZY RELATIONS n n Cartesian

CLASSICAL RELATIONS AND FUZZY RELATIONS

報告流程 n n 卡氏積 (Cartesian Product) 明確關係 (Crisp Relations) ¡ ¡ n 模糊關係 (Fuzzy Relations) ¡ ¡ ¡ n n n Cardinality Operations Properties 合成 (Composition) Cardinality Operations Properties Fuzzy Cartesian Product and Compositon Noninteractive Fuzzy Sets Crisp Tolerance and Equivalence Relations Fuzzy Tolerance and Equivalence Relations Value Assignments ¡ ¡ ¡ Cosine Amplitude Max-min Method Other Similarity Methods

Cartesian Product n n n Producing ordered relationships among sets X × Y = {(x, y)│x∈X, y∈Y} All the Ar = A ¡ A 1 × A 2 × ……. × Ar = Ar

Crisp Relations n n Measure by characteristic function：χ X × Y = {(x, y)│x∈X, y∈Y} ¡ ¡ ¡ Binary relation χX×Y(x, y)= 1, (x, y) ∈ X × Y 0, (x, y) X × Y χR(x, y)= 1, (x, y) ∈ X × Y 0, (x, y) X×Y

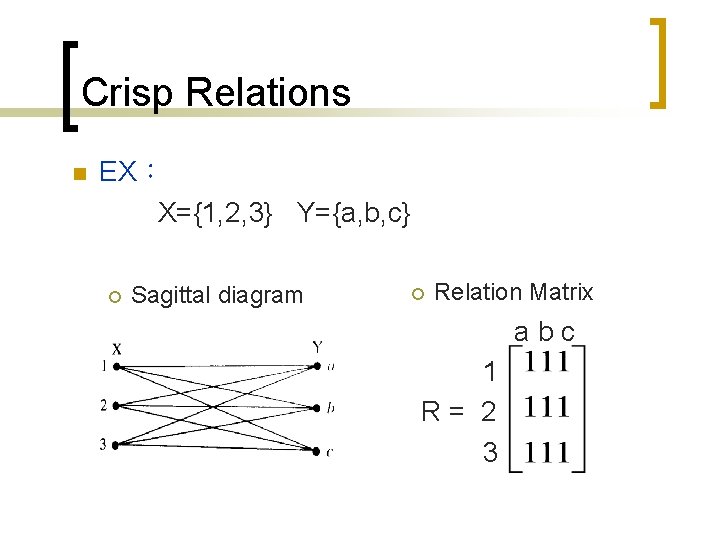
Crisp Relations n EX： X={1, 2, 3} Y={a, b, c} ¡ Sagittal diagram ¡ Relation Matrix abc 1 R= 2 3

Crisp Relations n Example 3. 2 ¡ (一) n n X={1, 2} Y={a, b} Locations of zero ¡ ¡ R={(1, a), (2, b)} 1 2 R a b X×Y (二) n n n A={0, 1, 2} UA：universal relation 以 A 2 為例 ¡ IA：identity relation UA = {(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)} IA = {(0, 0), (1, 1), (2, 2)}

Crisp Relations n Example 3. 3 ¡ ¡ ¡ Continous universes R={(x, y) | y ≥ 2 x, x∈X, y∈Y} χR(x, y)= 1, y ≥ 2 x 0, Y < 2 x

Cardinality of Crisp Relations n X：n elements Y：m elements n X ：the cardinality of X n Y ：the cardinality of Y ¡ Cardinality of the relation n ¡ n X × Y = n. X * n. Y power set n n The cardinality ：P(X × Y) n P(X × Y) = 2(n. Xn. Y)

Operations on Crisp Relations n Union n Intersection n Complement n Containment n Identity (Ø → O and X → E)

Properties of Crisp Relations n 交換律(Commutative law) n 結合律(Associative law) n 分配律(Distributive law) n n 乘方(Involution) 冪等律(Idempotence) n 狄摩根定律(De Morgan’s law) n 排中律(Low of Excluded Middle)

Composition n R={(X 1, Y 1), (X 1, Y 3), (X 2, Y 4)} S={(Y 1, Z 2), (Y 3, Z 2)} n Composition oeration ¡ Max-min composition n ¡ T=R。S Max-product comositon n T=R。S

Composition n Example 3. 4 ¡ Max-min composition y 1 y 2 y 3 y 4 z 1 z 2 R= x 1 S= y 1 x 2 y 2 x 3 y 4 z 1 z 2 T= x 1 x 2 x 3

Fuzzy Relations n Membership function ¡ ¡ n Interval [0, 1] Cartesian space X × Y => Cardinality of Fuzzy Relations ¡ Universe is infinity

Operations on Fuzzy Relations n Union ¡ n Intersection n Complement n Containment

Properties of Fuzy Relations n 排中律(Low of Excluded Middle)在 Fuzzy 集合中並不成立 !

Fuzzy Cartesian Product n Cartesian product space n Fuzzy relation n Example 3. 5 has membership function

Fuzzy Composition n Fuzzy max-min composition n Fuzzy max-product composition n 不論 crisp 或 fuzzy 的composition

Fuzzy Composition n Example 3. 6 X={x 1, x 2} Y={y 1, y 2} Z={z 1, z 2, z 3} ¡ Max-min composition ¡ Max-product compositon

Noninteractive Fuzzy Sets n Fuzzy set on the Cartesian space X =X 1 × X 2 noninteractive

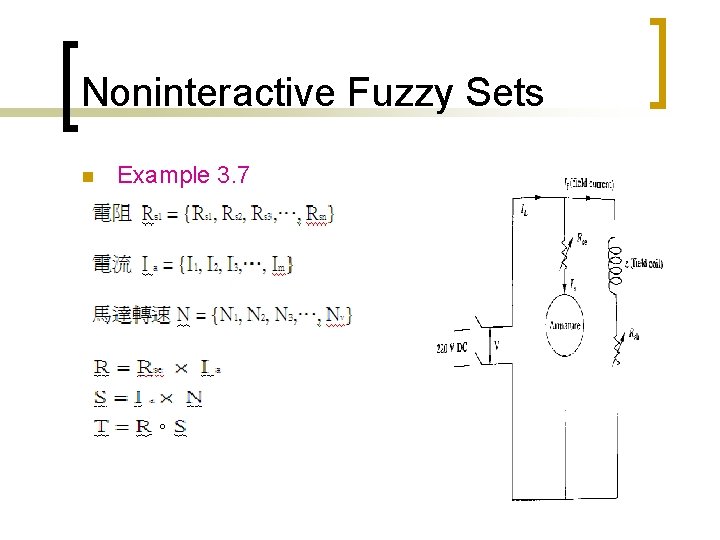
Noninteractive Fuzzy Sets n Example 3. 7

Noninteractive Fuzzy Sets n Example 3. 7(續) ¡ Cartesian product

Noninteractive Fuzzy Sets n Example 3. 7(續) ¡ n Max-min composition Example 3. 8 ¡ Max-min composition

Noninteractive Fuzzy Sets n Example 3. 9

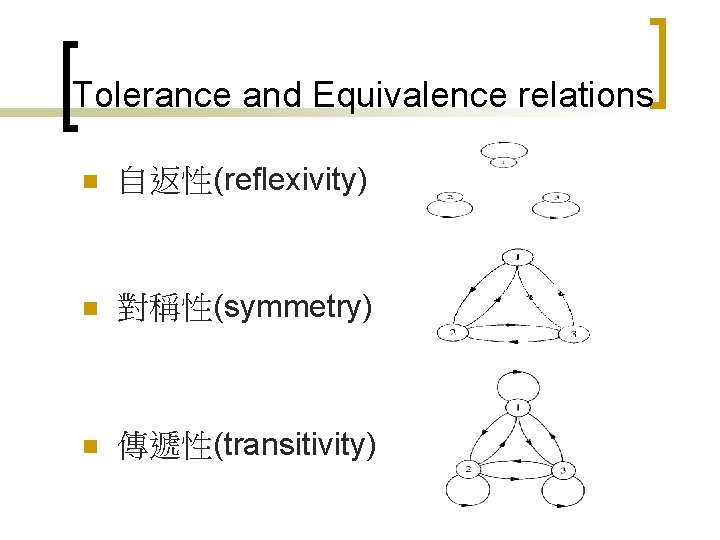
Tolerance and Equivalence relations n 自返性(reflexivity) n 對稱性(symmetry) n 傳遞性(transitivity)

Crisp Eqivalence Relation n 自返性(reflexivity) ¡ n R or 對稱性(symmetry) ¡ n (xi, xi) (xi, xj) or R (xj, xi) R 傳遞性(transitivity) ¡ (xi, xj) or R and (xj, xk) R (xi, xk) R

Crisp Tolerance Relation n Also called proximity relation Only the reflexivity and symmetry Can be reformed into an equivalence relation ¡ By at most (n-1) compositions with itself

Crisp Tolerance Relation n Example 3. 10 ¡ X={x 1, x 2, x 3, x 4, x 5}={Omaha, Chicago, Rome, London, Detroit} ¡ R 1 does not properties of transitivity n e. g. (x 1, x 2) R 1 (x 2, x 5) R 1 but (x 1, x 5) R 1

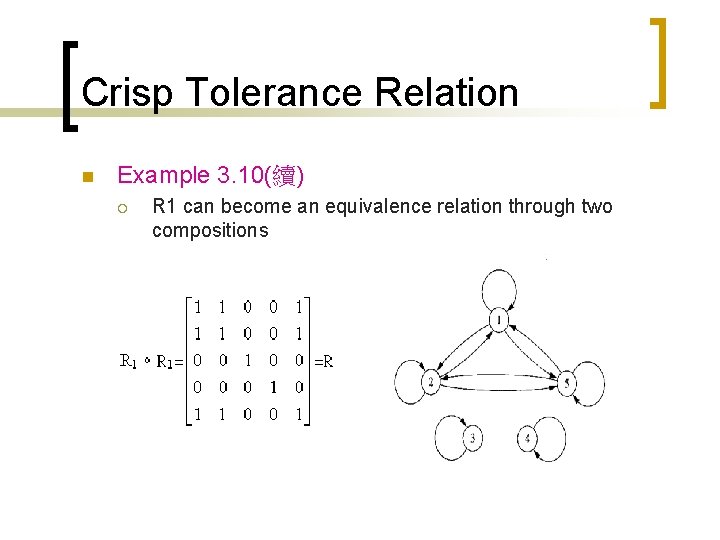
Crisp Tolerance Relation n Example 3. 10(續) ¡ R 1 can become an equivalence relation through two compositions

Fuzzy tolerance and equivalence relations n 自返性(reflexivity) n 對稱性(symmetry) n 傳遞性(transitivity)

Fuzzy tolerance and equivalence relations n Equivalence relations ¡ Fuzzy tolerance relation Can be reformed into an equivalence relation n By at most (n-1) compositions with itself

Fuzzy tolerance and equivalence relations n Example 3. 11 ¡ ¡ It is not transitive ¡ One composition Reflexive and symmetric

Fuzzy tolerance and equivalence relations n Example 3. 11(續)

Value assignments n n Cartesian product Closed-from expression ¡ ¡ Simple observation of a physical process No variation n Lookup table ¡ Variability exist n n Membership values on the interval [0, 1] Develop a fuzzy relation Linguistic rules of knowledge ¡ n model the process crisp relation Y= f(X) If-then rules Classification Similarity methods in data manipulation

Cosine Amplitude n X={x 1, x 2, …. , xn} xi={ }

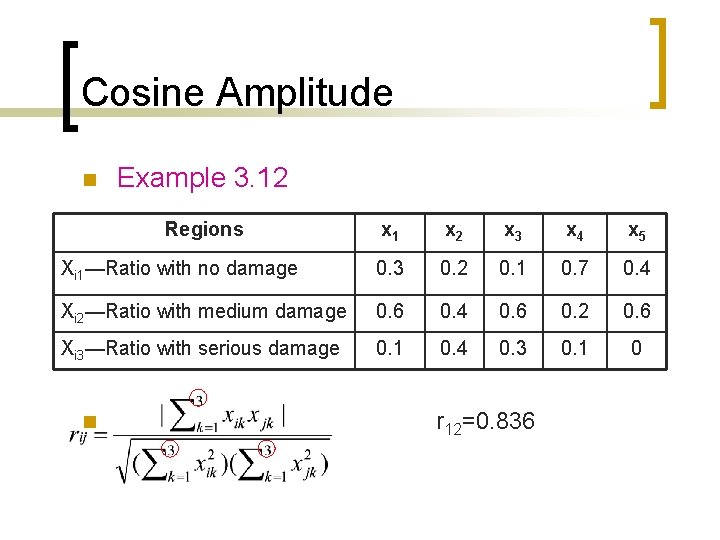
Cosine Amplitude n Example 3. 12 Regions x 1 x 2 x 3 x 4 x 5 Xi 1—Ratio with no damage 0. 3 0. 2 0. 1 0. 7 0. 4 Xi 2—Ratio with medium damage 0. 6 0. 4 0. 6 0. 2 0. 6 Xi 3—Ratio with serious damage 0. 1 0. 4 0. 3 0. 1 0 n r 12=0. 836

Cosine Amplitude n Example 3. 12(續) ¡ Tolerance relation ¡ Equivalence relation

Max-min Method n rij= n Example 3. 13 ¡ where i, j =1, 2, …n Reconsider Example 3. 12 n Tolerance relation

Summary Q&A