Classical Principles of Electromagnetism Electric and magnetic field

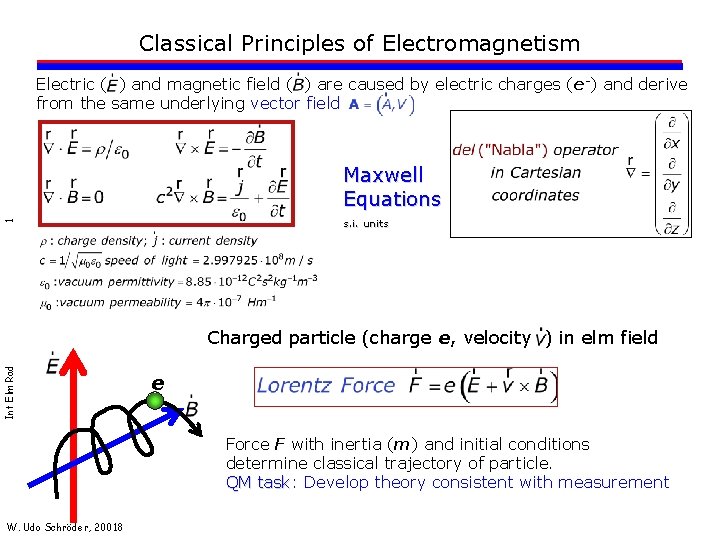
Classical Principles of Electromagnetism Electric ( ) and magnetic field ( ) are caused by electric charges (e-) and derive from the same underlying vector field Maxwell Equations 1 s. i. units Int Elm Rad Charged particle (charge e, velocity ) in elm field e Force F with inertia (m) and initial conditions determine classical trajectory of particle. QM task: task Develop theory consistent with measurement W. Udo Schröder, 20018

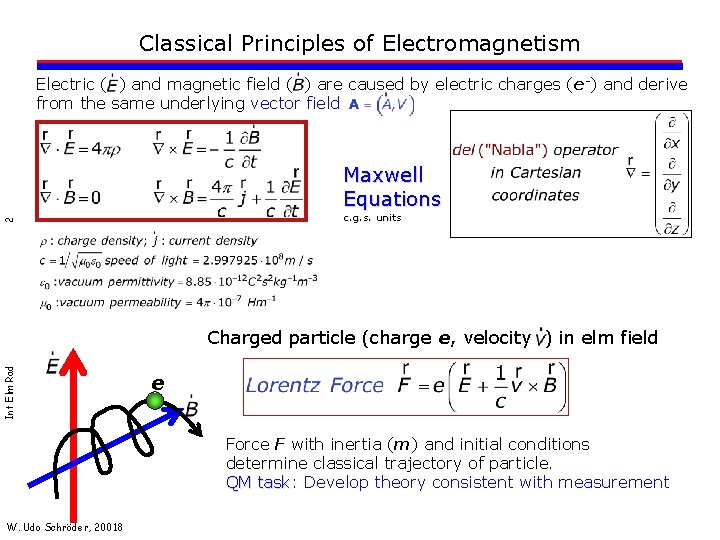
Classical Principles of Electromagnetism Electric ( ) and magnetic field ( ) are caused by electric charges (e-) and derive from the same underlying vector field Maxwell Equations 2 c. g. s. units Int Elm Rad Charged particle (charge e, velocity ) in elm field e Force F with inertia (m) and initial conditions determine classical trajectory of particle. QM task: task Develop theory consistent with measurement W. Udo Schröder, 20018

QM: Charged-Particle Coupling to Elm Field Int Elm Rad 3 e Larger task: task Derive an internally consistent quantum mechanical account of the properties of field quanta and interactions with particles. W. Udo Schröder, 20018

Charged Particles in Elm Fields Int Elm Rad 4 Explain, or model, Lorentz force on particle (mass m, charge e): Non-conservative, velocity (v) dependent force effective potential W. Udo Schröder, 20018

Int Elm Rad 5 Minimum Coupling to Field Schrödinger Equation for charged (e) particle in elm field W. Udo Schröder, 20018

1 st Order Interaction Hamiltonian Int Elm Rad 6 First term is kinetic energy of free, unperturbed particle. Last term is of second order in field A, neglect in first order estimate. Interaction Hamiltonian of particle (mass m, charge q, magnetic moment m) with time dependent elm. field. Add ad hoc spin magnetic interaction Make real by adding complex conjugate CC. W. Udo Schröder, 20018 Larmor frequency.

Int Elm Rad 7 More Degrees of Freedom Since mp ≈2000·me, electronic terms are dominant for atoms and molecules. W. Udo Schröder, 20018

Application in Perturbation Theory 8 Interaction Hamiltonian of particle (mass m, charge q, magnetic moment m) with time dependent elm. field. Int Elm Rad Use in perturbation theory, single-photon emission or absorption W. Udo Schröder, 20018

Int Elm Rad 9 Hint with spin and orbital mu W. Udo Schröder, 20018