Classical Model of Rigid Rotor A particle rotating
















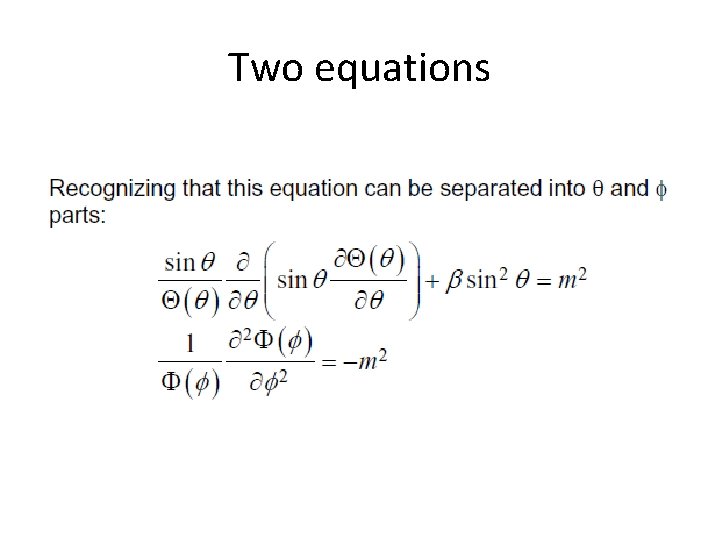

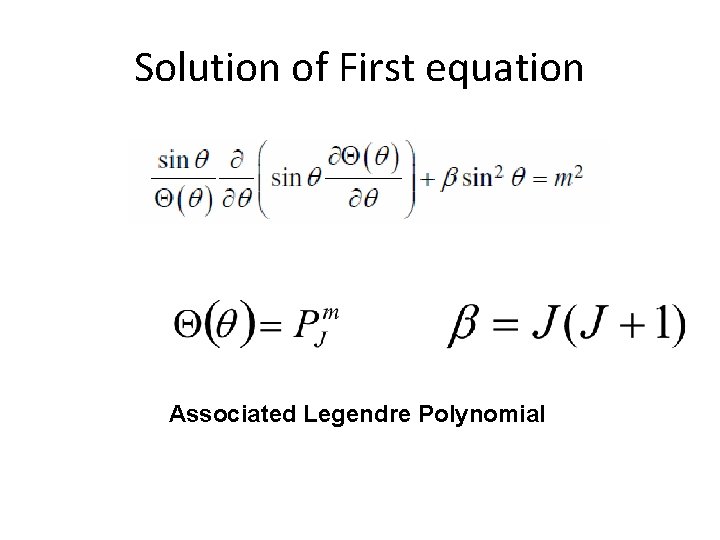



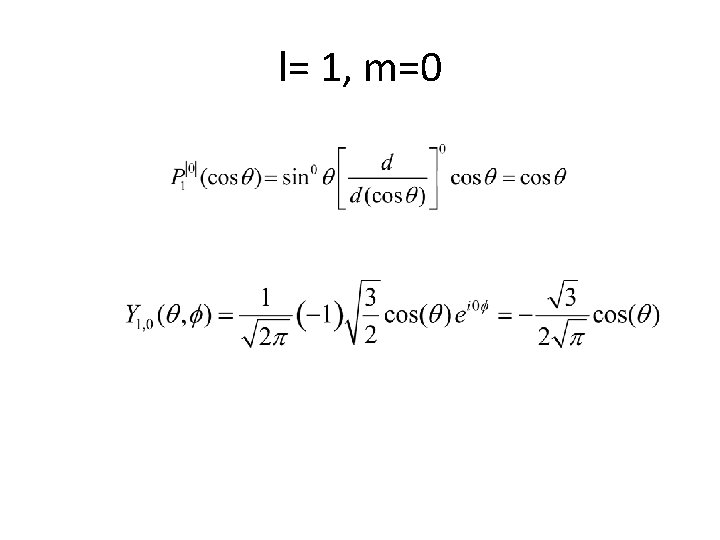








- Slides: 38

Classical Model of Rigid Rotor A particle rotating around a fixed point, as shown below, has angular momentum and rotational kinetic energy (“rigid rotor”) The classical kinetic energy is given by: If the particle is rotating about a fixed point at radius r with a frequency ʋ (s − 1 or Hz), the velocity o the particle is given by: where ω is the angular frequency (rad s− 1 or rad Hz). The rotational kinetic energy can be now expressed as: Also where

Consider a classical rigid rotor corresponding to a diatomic molecule. Here we consider only rotation restricted to a 2 -D plane where the two masses (i. e. , the nuclei) rotate about their center of mass. The rotational kinetic energy for diatomic molecule in terms of angular momentum Note that there is no potential energy involved in free rotation.

Momentum Summary Classical Linear Momentum Energy Rotational Momentum (Angular) Energy QM

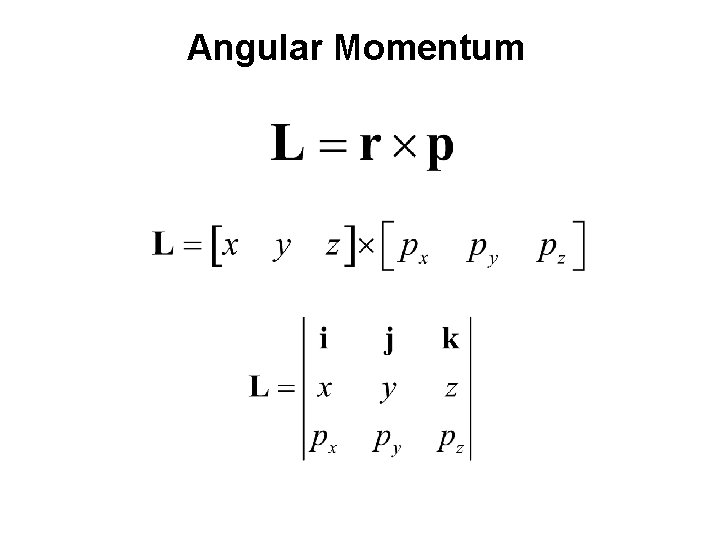
Angular Momentum

Angular Momentum

Angular Momentum

Angular Momentum

Two-Dimensional Rotational Motion Polar Coordinates y r f x

Two-Dimensional Rotational Motion

Two-Dimensional Rigid Rotor Assume r is rigid, ie. it is constant

Two-Dimensional Rigid Rotor

Solution of equation

Energy and Momentum As the system is rotating about the z-axis

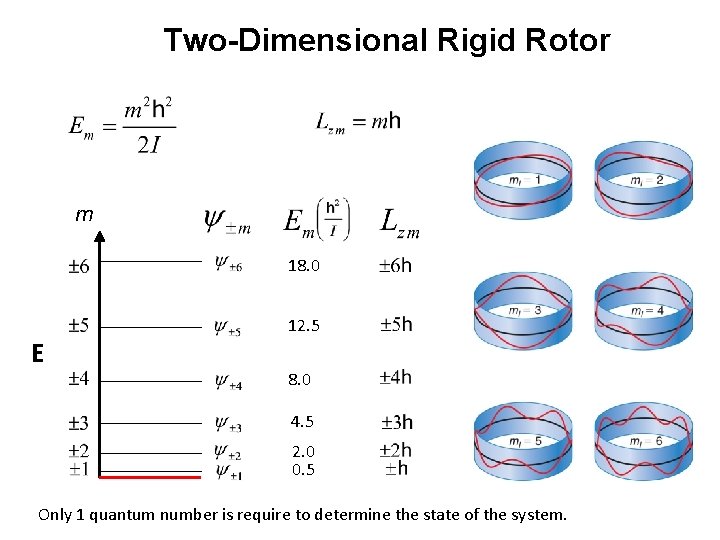
Two-Dimensional Rigid Rotor m 18. 0 12. 5 E 8. 0 4. 5 2. 0 0. 5 Only 1 quantum number is require to determine the state of the system.

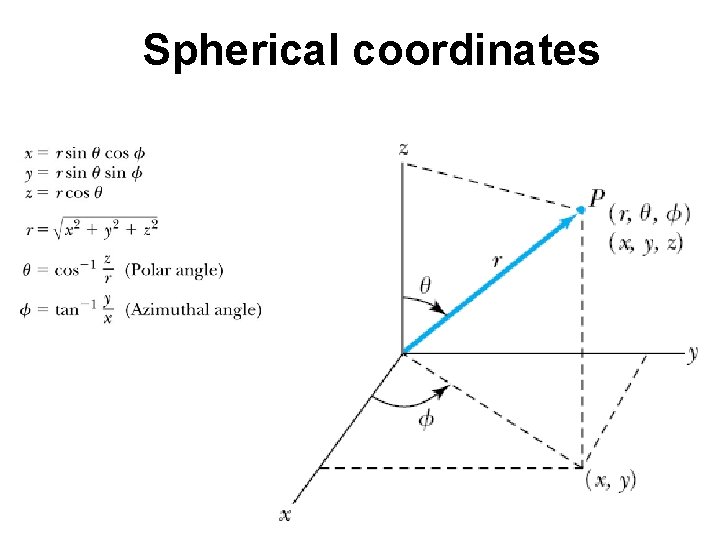
Spherical coordinates

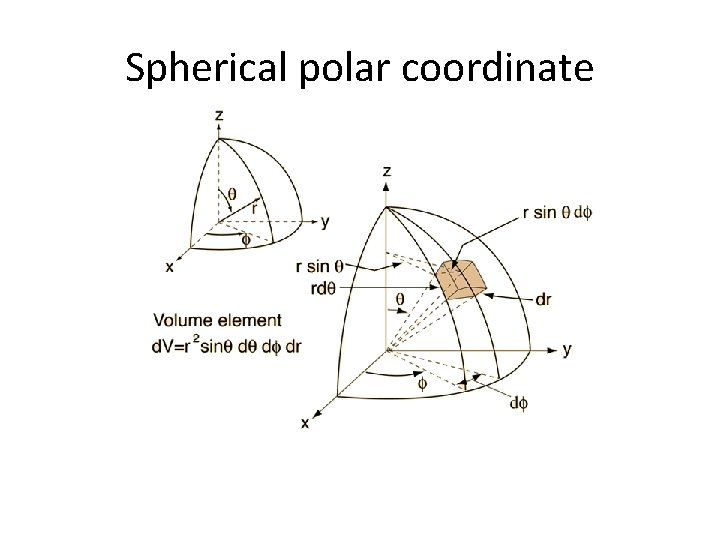
Spherical polar coordinate

Hamiltonian in spherical polar coordinate

Rigid Rotor in Quantum Mechanics Transition from the above classical expression to quantum mechanics can be carried out by replacing the total angular momentum by the corresponding operator: Wave functions must contain both θ and Φ dependence: are called spherical harmonics

Schrondinger equation

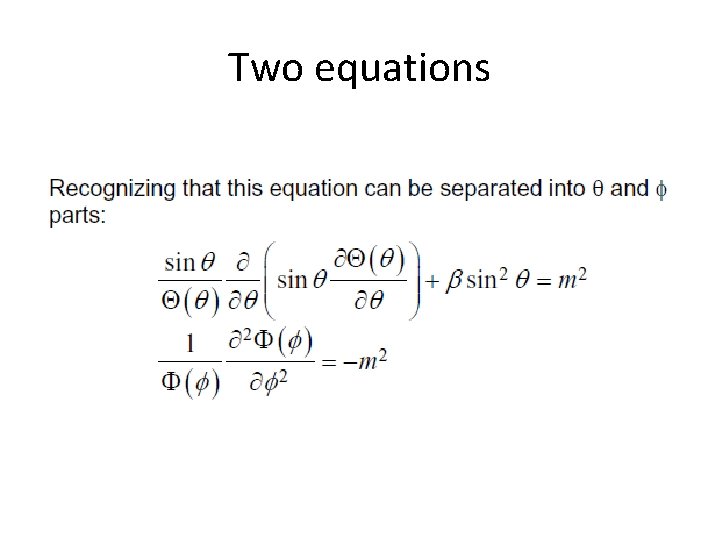
Two equations

Solution of second equation
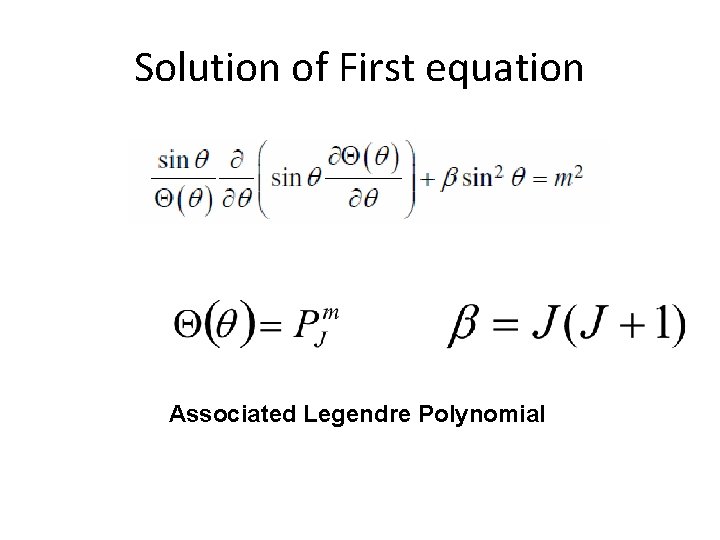
Solution of First equation Associated Legendre Polynomial

Associated Legendre Polynomial

For l=0, m=0

First spherical harmonics Spherical Harmonic, Y 0, 0
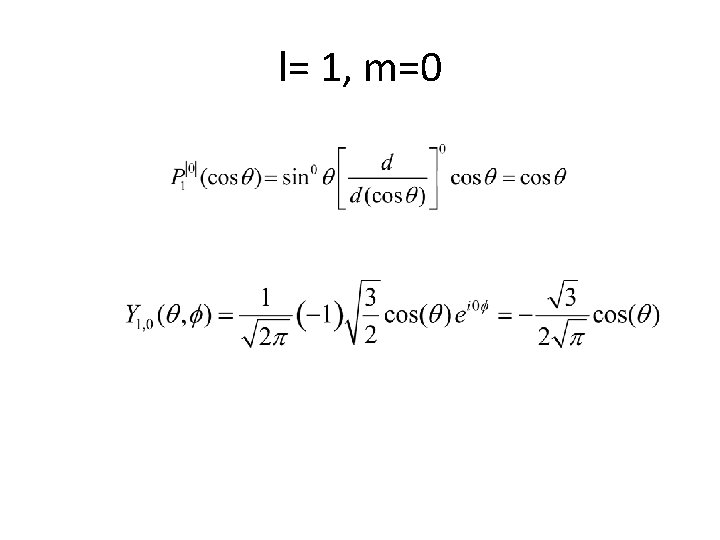
l= 1, m=0

l= 1, m=0 θ cos 2θ 0 1 30 3/4 45 1/2 60 1/4 90 0

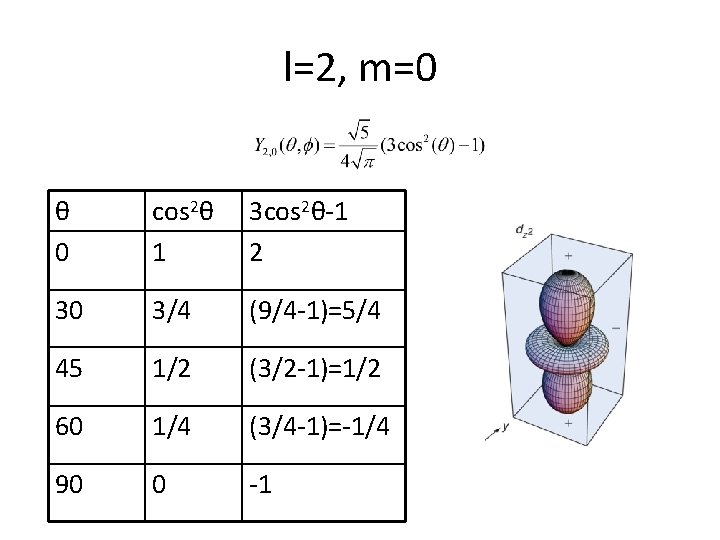
l=2, m=0 θ 0 cos 2θ 1 3 cos 2θ-1 2 30 3/4 (9/4 -1)=5/4 45 1/2 (3/2 -1)=1/2 60 1/4 (3/4 -1)=-1/4 90 0 -1

l = 1, m=± 1 Complex Value? ? If Ф 1 and Ф 2 are degenerateeigenfunctions, their linear combinations are also an eigenfunction with the same eigenvalue.

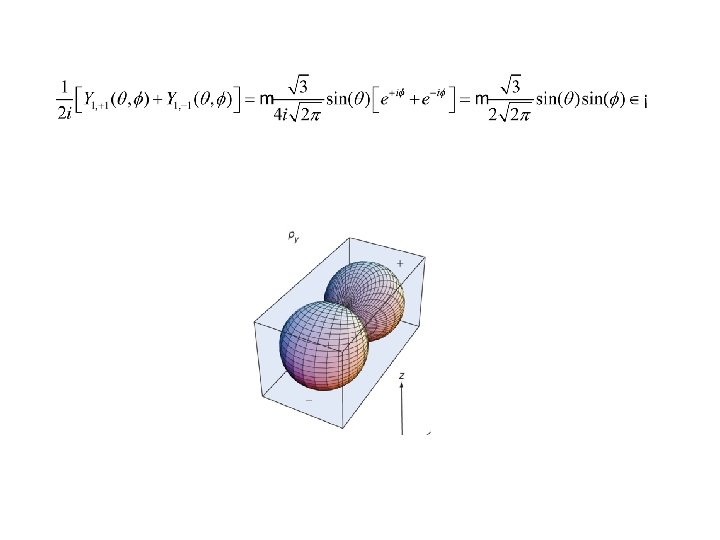
l=1, m=± 1 Along x-axis




E Three-Dimensional Rigid Rotor States l m 32 2 10 -1 -2 -3 6. 0 10 -1 -2 3. 0 1 0 -1 0 1. 0 0. 5 Only 2 quantum numbers are required to determine the state of the system.

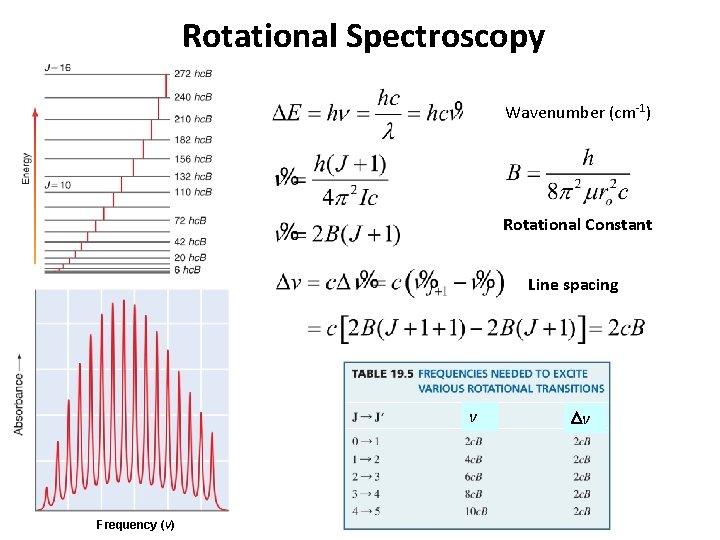
Rotational Spectroscopy J : Rotational quantum number Rotational Constant

Rotational Spectroscopy Wavenumber (cm-1) Rotational Constant Line spacing v Frequency (v) Dv

Bond length • To a good approximation, the microwave spectrum of H 35 Cl consists of a series of equally spaced lines, separated by 6. 26*1011 Hz. Calculate the bond length of H 35 Cl.