CLASSICAL EXAMPLE MATRIX MULTIPLICATION Run time On 3

CLASSICAL EXAMPLE: MATRIX MULTIPLICATION Run time: O(n 3) in the naïve implementation 1. n = A. rows 2. Let C be a new n by n matrix 3. for i=1 to n 4. for j=1 to n 5. cij = 0 6. for k=1 to n 7. cij = cij+ aik bkj 8. return C CSC 317 Can we do better? 1

CLASSICAL EXAMPLE: MATRIX MULTIPLICATION Divide and conquer? • Can’t break in half like array • But can break into 4 pieces CSC 317 2

CLASSICAL EXAMPLE: MATRIX MULTIPLICATION Divide and conquer? • Can’t break in half like array • But can break into 4 pieces CSC 317 3

CLASSICAL EXAMPLE: MATRIX MULTIPLICATION Now each capital A; B; C is a whole square matrix (need not be a single element) CSC 317 4

CLASSICAL EXAMPLE: MATRIX MULTIPLICATION • Now each capital A; B; C is a whole square matrix (need not be a single element) • Write out what the elements C 11, C 12, C 21, C 22 are in terms of A and B? CSC 317 5

How many recursive calls to matrix multiply? 8 total multiplications = 8 recursive calls CSC 317 6

How many recursive calls to matrix multiply? 8 total multiplications = 8 recursive calls Cost of combining recursions? 4 matrix additions, each matrix size n 2/4 CSC 317 7

• Divide: constant time • Conquer: 8 matrix multiplications of size • Combine: 4 matrix additions, each has size Total: CSC 317 8

• Divide: constant time • Conquer: 8 matrix multiplications of size • Combine: 4 matrix additions, each has size Total: Cost? Guess? Answer: Bad news! But how (will talk about it after recursions)? CSC 317 9

Strassen’s method Clever way to compute only 7 matrix multiplications and therefore 7 recursions By defining new matrices that are sums and differences of the original But how? CSC 317 10

Strassen’s method What is this clever solution? 1. ) Use the submatrices of A and B as before. 2. ) Define additions and subtractions of the submatrices 10 additions and subtractions CSC 317 11

Strassen’s method 3. ) Recursively, compute 7 matrices 7 multiplications instead of 8 CSC 317 12

Strassen’s method 4. ) Compute desired C 11, C 12, C 21, C 22 by adding and subtracting combinations of P matrices Example 0 CSC 317 13

Matrix multiplication – if recursion helps or hurts not always intuitive • Naïve • Simple divide and conquer • Strassen’s divide and conquer method Anybody confused now? We’d like to better understand what determines cost of divide and conquer approaches CSC 317 14

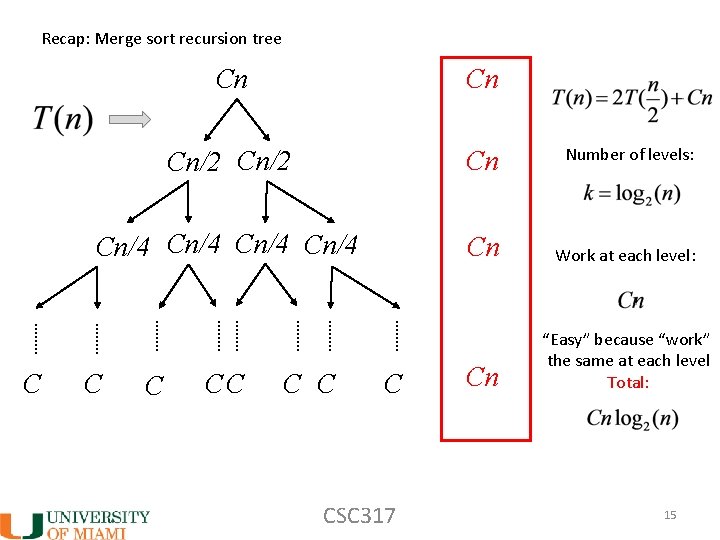
Recap: Merge sort recursion tree C Cn Cn Cn/2 Cn Number of levels: Cn/4 Cn Work at each level: Cn “Easy” because “work” the same at each level Total: C C C C CSC 317 15

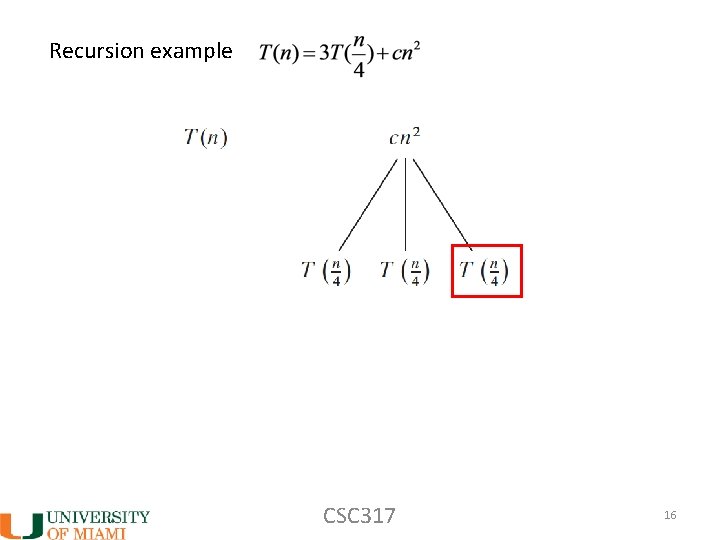
Recursion example CSC 317 16

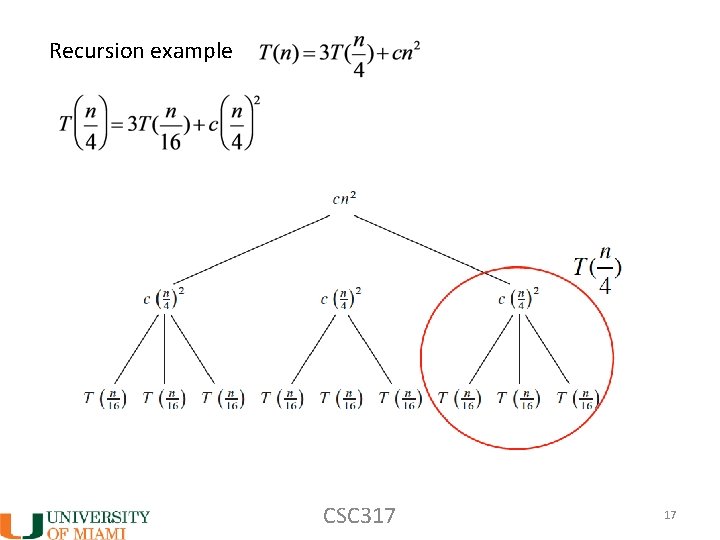
Recursion example CSC 317 17

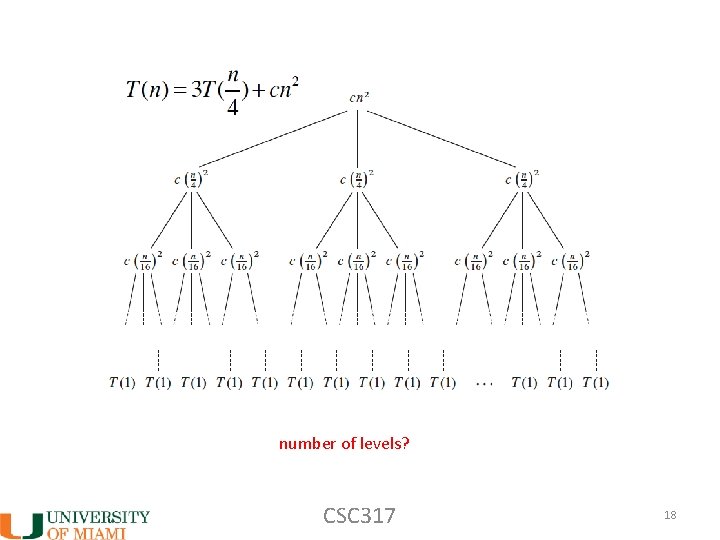
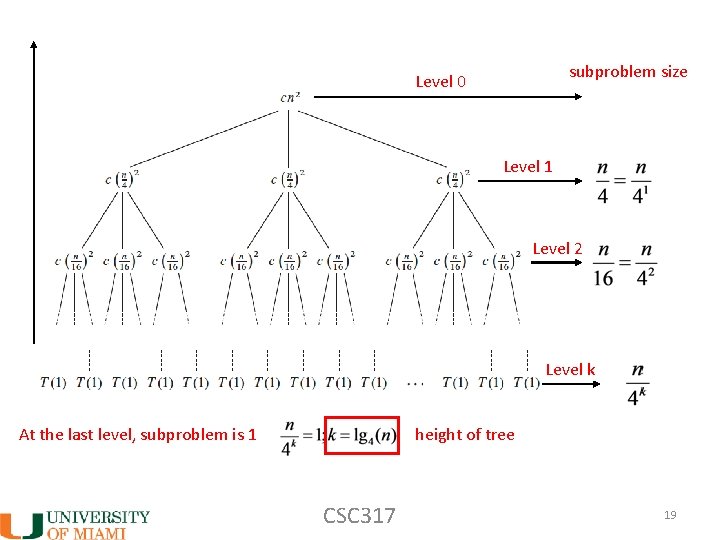
number of levels? CSC 317 18

subproblem size Level 0 Level 1 Level 2 Level k At the last level, subproblem is 1 height of tree CSC 317 19

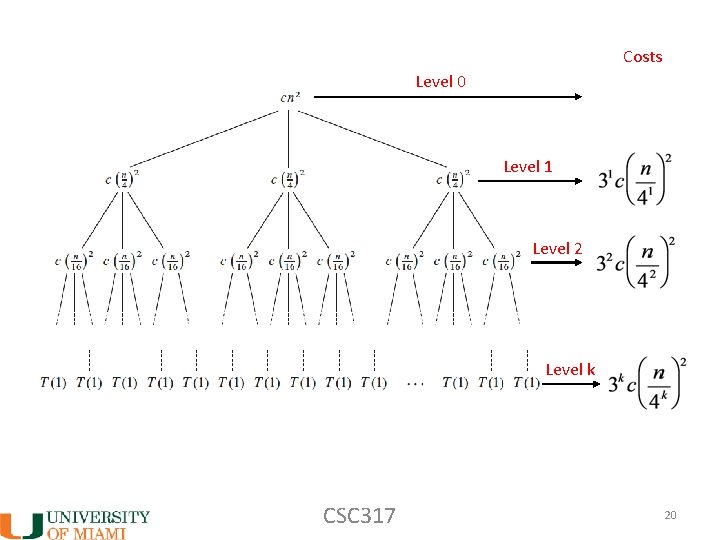
Costs Level 0 Level 1 Level 2 Level k CSC 317 20

Cost at level k: Cost at last level? We know we are down to subproblem size of 1. We just need to know the number of nodes Remember: since so: Cost at last level: CSC 317 21

Total work? last level all other levels This can be solved exactly (messy), but … CSC 317 22

… we also know that for an Infinite summation series and |x|<1 but our series does not go to ∞ … We could use it as an upper bound! CSC 317 23

Total work

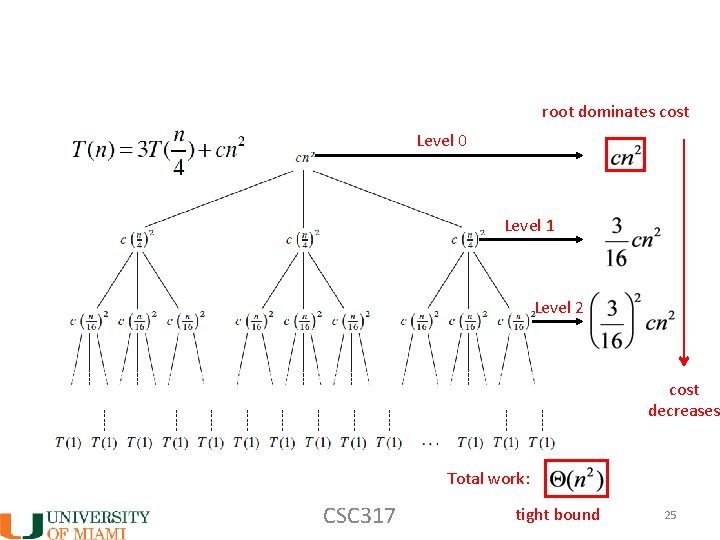
root dominates cost Level 0 Level 1 Level 2 cost decreases Total work: CSC 317 tight bound 25

Equal costs at all levels Root dominated Leave dominated CSC 317 26