Classical Density Functional Theory of Solvation in Molecular

Classical Density Functional Theory of Solvation in Molecular Solvents Daniel Borgis Département de Chimie Ecole Normale Supérieure de Paris daniel. borgis@ens. fr • Rosa Ramirez (Université d’Evry) • Shuangliang Zhao (ENS Paris)

Solvation: Some issues For a given molecule in a given solvent, can we predict efficiently and with « chemical accuracy: • The solvation free energy • The microscopic solvation profile A few applications: • Differential solvation (liquid-liquid extraction) • Solubility prediction • Reactivity • Biomolecular solvation, …. Explicit solvent/FEP

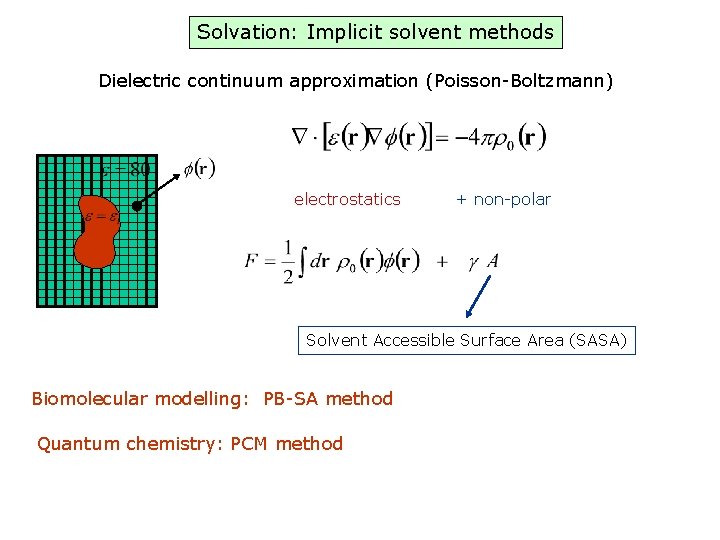
Solvation: Implicit solvent methods Dielectric continuum approximation (Poisson-Boltzmann) electrostatics + non-polar Solvent Accessible Surface Area (SASA) Biomolecular modelling: PB-SA method Quantum chemistry: PCM method

Improved implicit solvent models (based on « modern » liquid state theory) • Integral equations • Interaction site picture (RISM) (D. Chandler, P. Rossky, M. Pettit, F. Hirata, A. Kovalenko) Site-site OZ + closure • Molecular picture (G. Patey, P. Fries, …) Molecular OZ + closure • Classical Density Functional Theory This work: Can we use classical DFT to define an improved and well-founded implicit solvation approach?

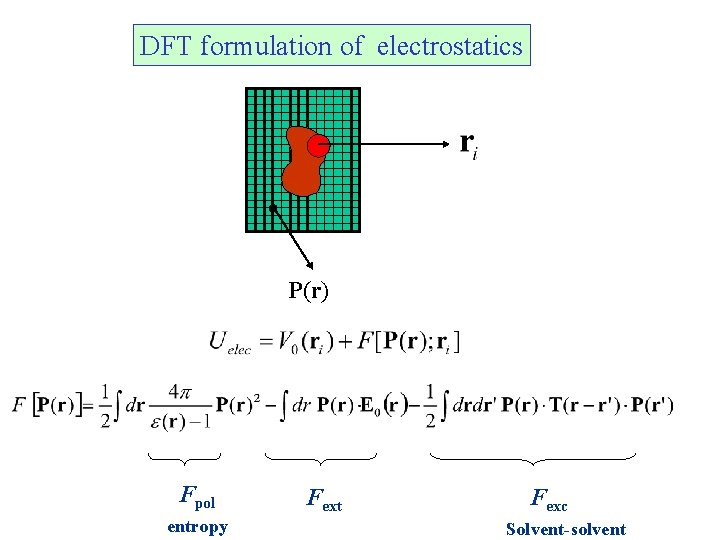
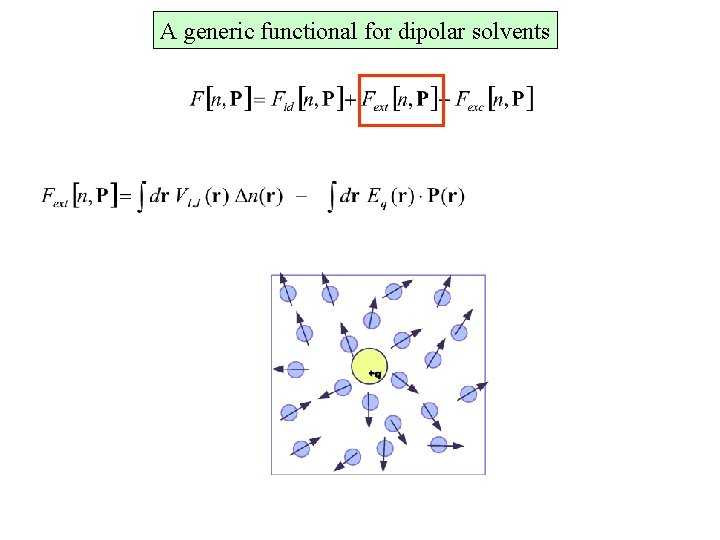
DFT formulation of electrostatics P(r) Fpol entropy Fext Fexc Solvent-solvent

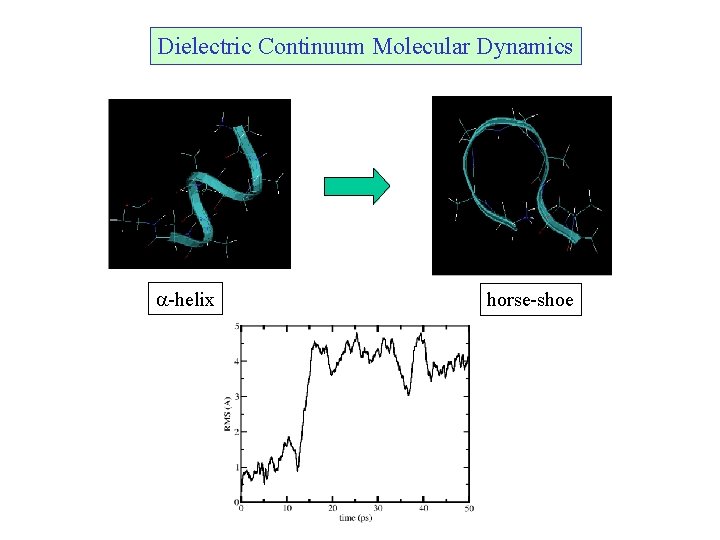
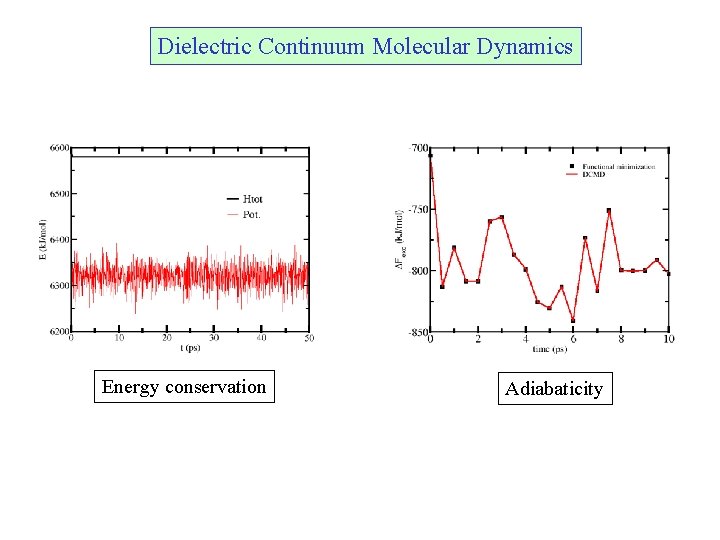
Dielectric Continuum Molecular Dynamics M. Marchi, DB, et al. , J. Chem Phys. (2001), Comp. Phys. Comm. (2003) Use analogy with electronic DFT calculations and CPMD method Plane wave expansion Soft « pseudo-potentials » On-the-fly minimization with extended Lagrangian

Dielectric Continuum Molecular Dynamics a-helix horse-shoe

Dielectric Continuum Molecular Dynamics Energy conservation Adiabaticity

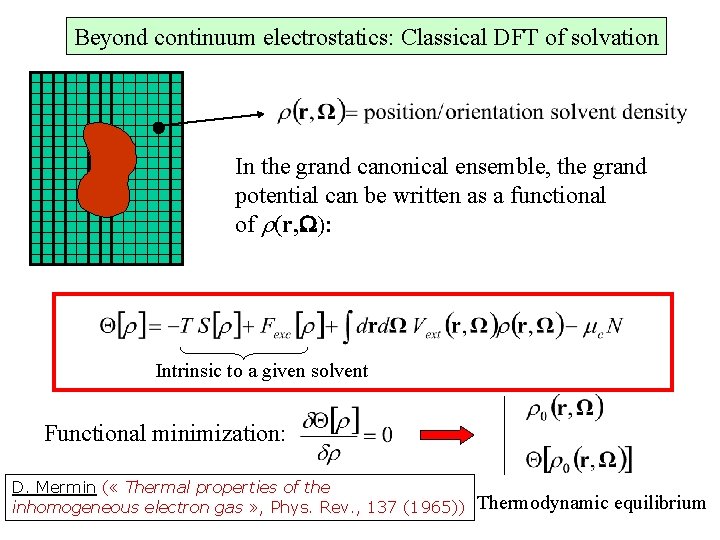
Beyond continuum electrostatics: Classical DFT of solvation In the grand canonical ensemble, the grand potential can be written as a functional of r(r, W): Intrinsic to a given solvent Functional minimization: D. Mermin ( « Thermal properties of the inhomogeneous electron gas » , Phys. Rev. , 137 (1965)) Thermodynamic equilibrium

In analogy to electronic DFT, how to use classical DFT as a « theoretical chemist » tool to compute the solvation properties of molecules, in particular their solvation free-energy ? But what is the functional ? ?

The exact functional

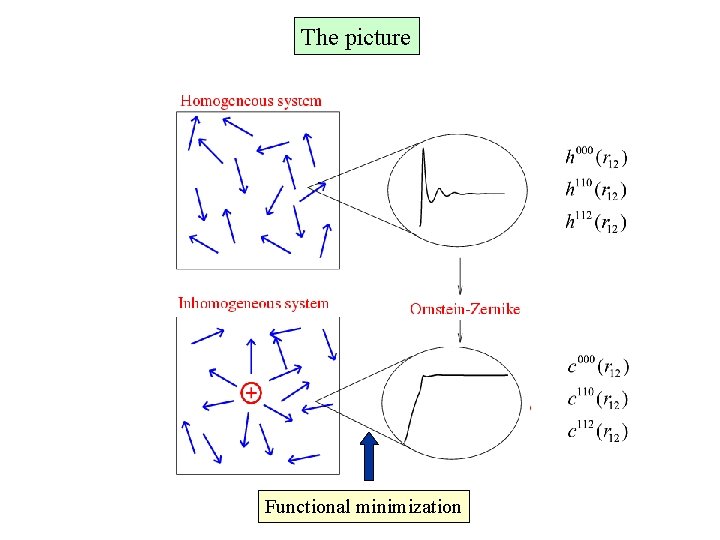
The homogeneous reference fluid approximation Neglect the dependence of c(2)(x 1, x 2, [ra]) on the parameter a, i. e use direct correlation function of the homogeneous system c(x 1, x 2) connected to the pair correlation function h(x 1, x 2) through the Ornstein-Zernike relation g(r) h(r)

The homogeneous reference fluid approximation Neglect the dependence of c(2)(x 1, x 2, [ra]) on the parameter a, i. e use direct correlation function of the homogeneous system c(x 1, x 2) connected to the pair correlation function h(x 1, x 2) through the Ornstein-Zernike relation g(r) h(r)

The picture Functional minimization

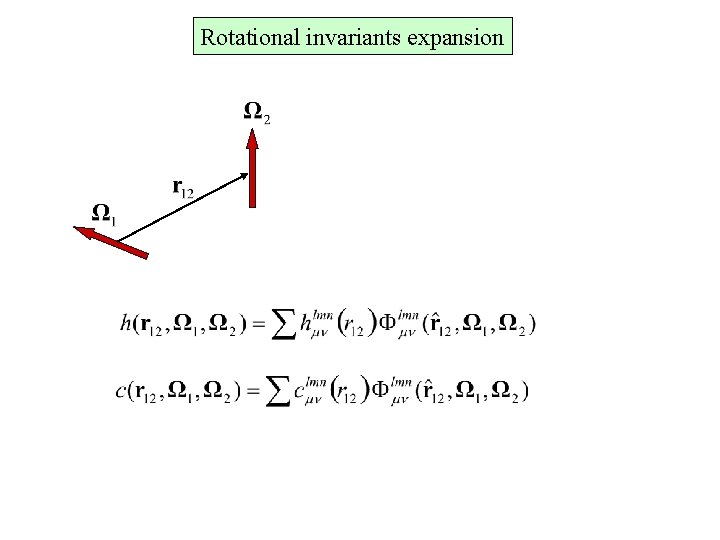
Rotational invariants expansion

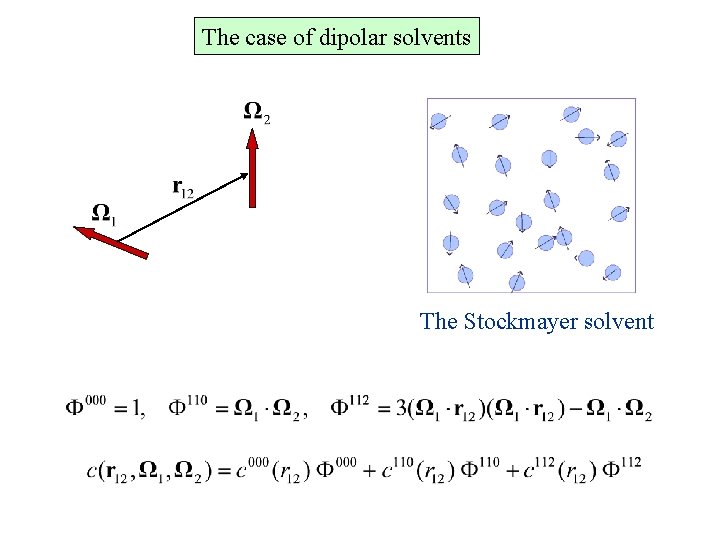
The case of dipolar solvents The Stockmayer solvent

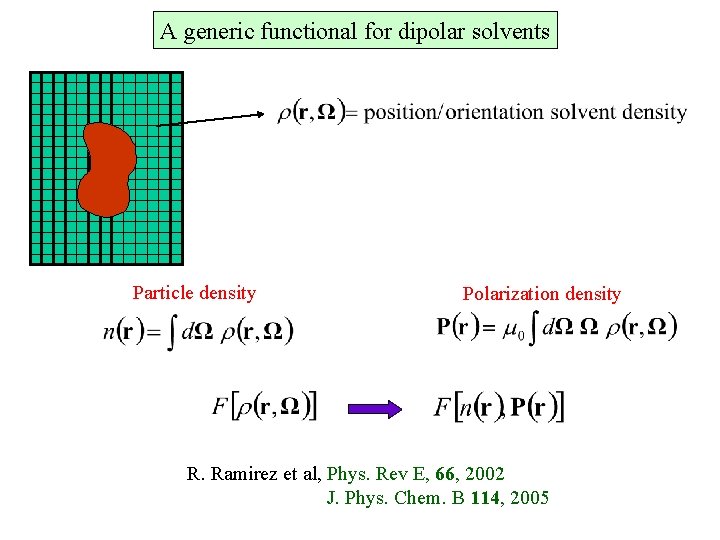
A generic functional for dipolar solvents Particle density Polarization density R. Ramirez et al, Phys. Rev E, 66, 2002 J. Phys. Chem. B 114, 2005

A generic functional for dipolar solvents

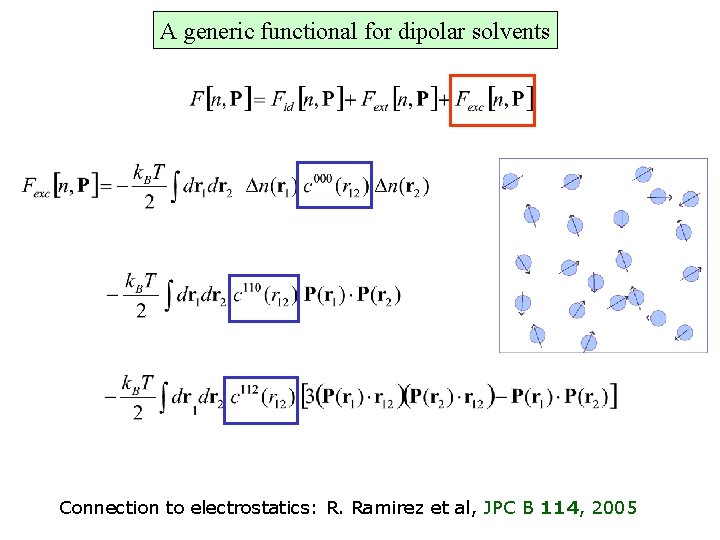
A generic functional for dipolar solvents

A generic functional for dipolar solvents

A generic functional for dipolar solvents Connection to electrostatics: R. Ramirez et al, JPC B 114, 2005

The picture Functional minimization

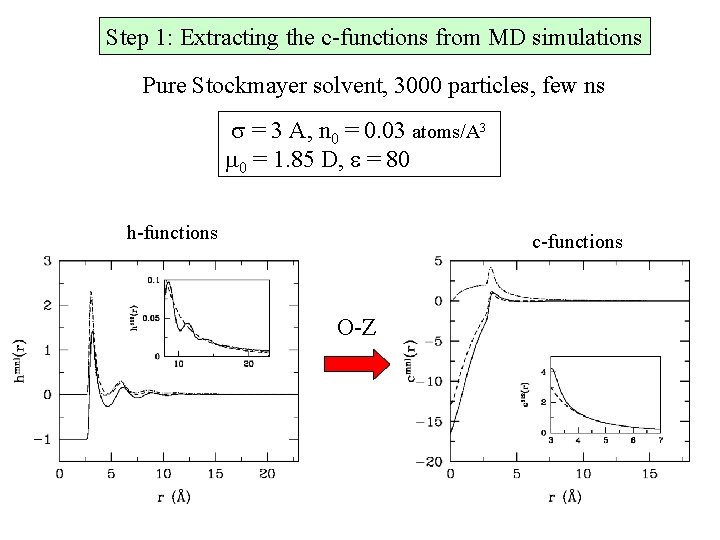
Step 1: Extracting the c-functions from MD simulations Pure Stockmayer solvent, 3000 particles, few ns s = 3 A, n 0 = 0. 03 atoms/A 3 m 0 = 1. 85 D, e = 80 h-functions c-functions O-Z

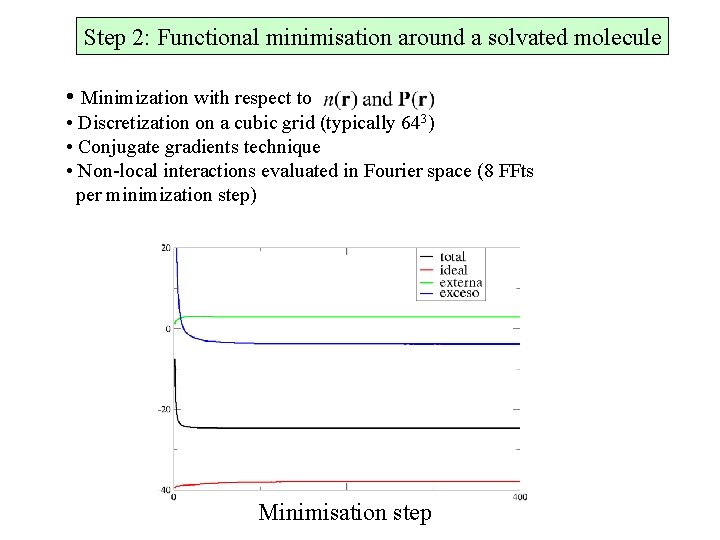
Step 2: Functional minimisation around a solvated molecule • Minimization with respect to • Discretization on a cubic grid (typically 643) • Conjugate gradients technique • Non-local interactions evaluated in Fourier space (8 FFts per minimization step) Minimisation step

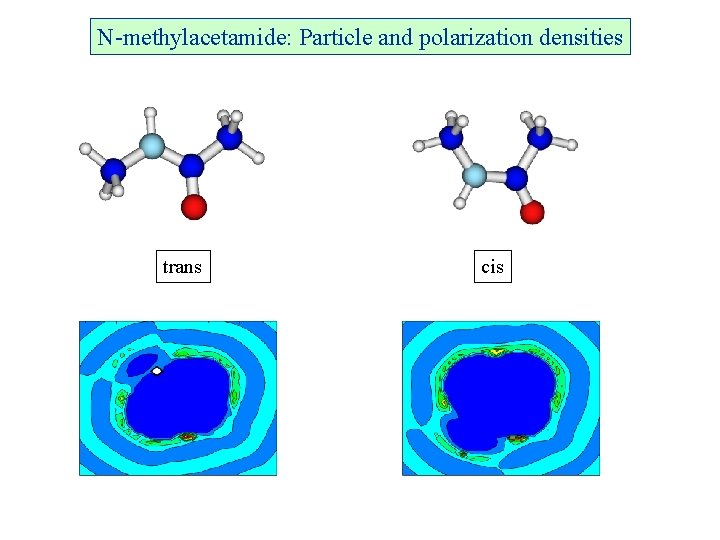
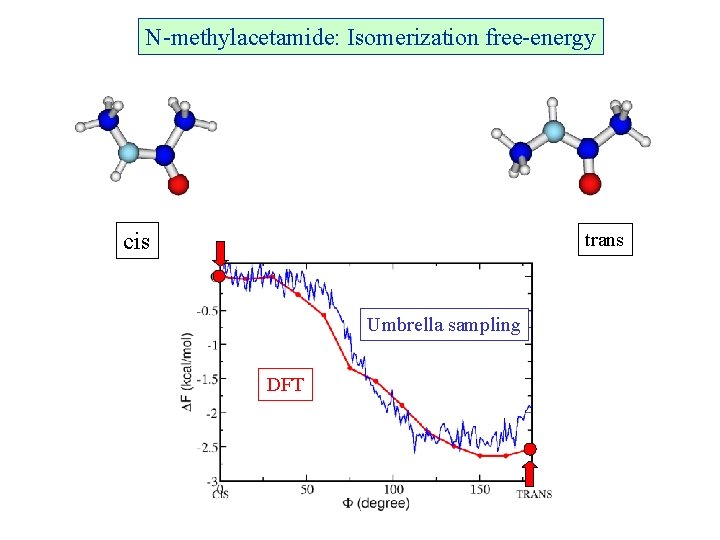
N-methylacetamide: Particle and polarization densities trans cis

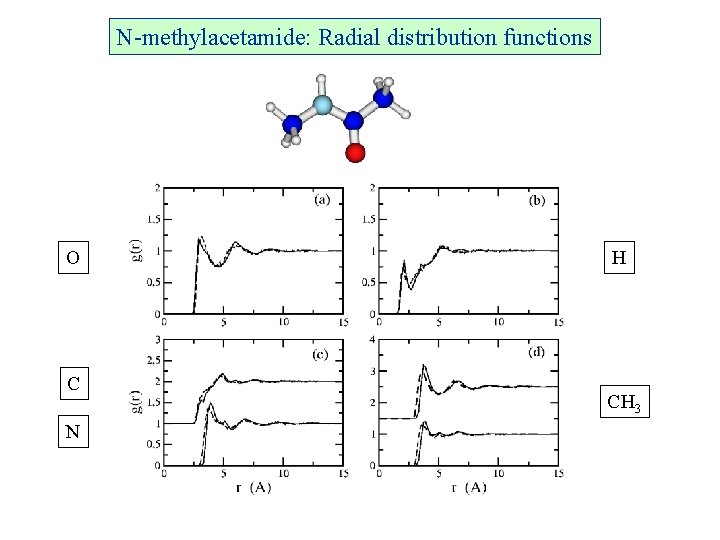
N-methylacetamide: Radial distribution functions O C N H CH 3

N-methylacetamide: Isomerization free-energy cis trans Umbrella sampling DFT

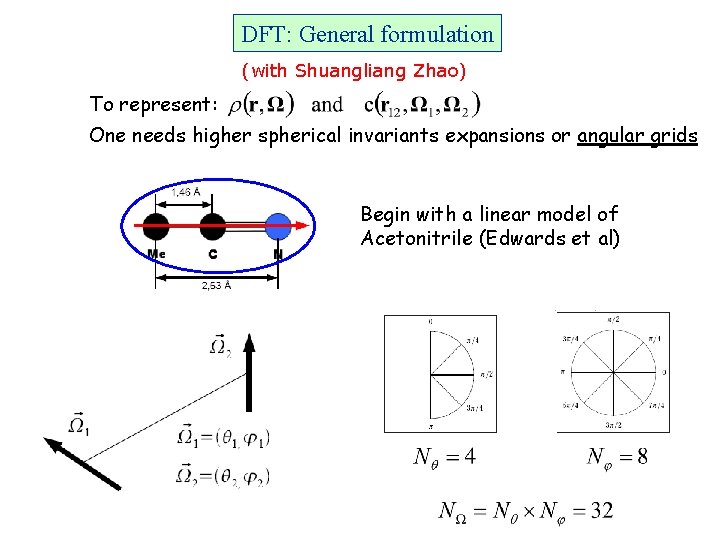
DFT: General formulation (with Shuangliang Zhao) To represent: One needs higher spherical invariants expansions or angular grids Begin with a linear model of Acetonitrile (Edwards et al)

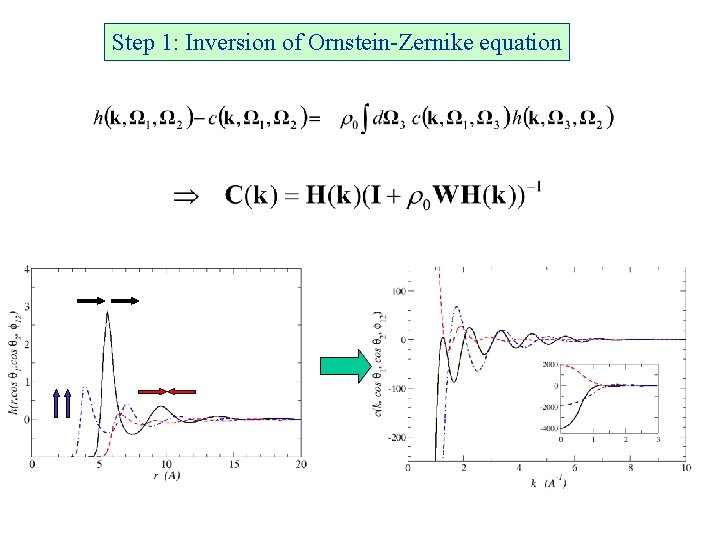
Step 1: Inversion of Ornstein-Zernike equation

Step 2: Minimization of the discretized functional Vexc(r 1, W 1)

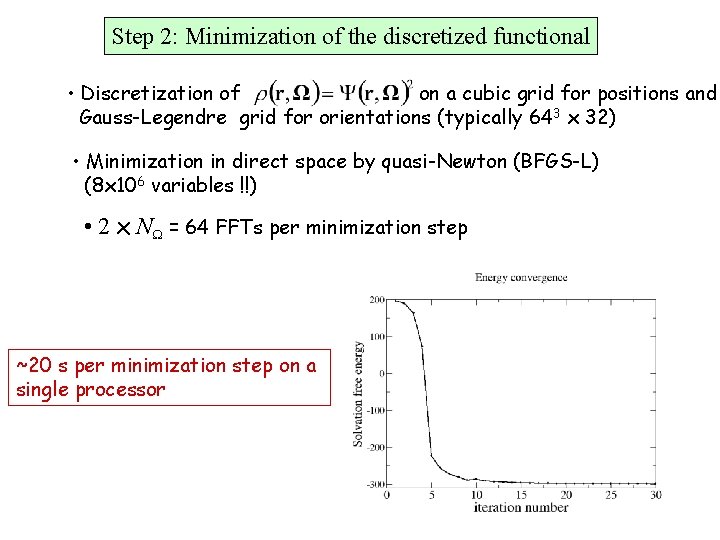
Step 2: Minimization of the discretized functional • Discretization of on a cubic grid for positions and Gauss-Legendre grid for orientations (typically 643 x 32) • Minimization in direct space by quasi-Newton (BFGS-L) (8 x 106 variables !!) • 2 x NW = 64 FFTs per minimization step ~20 s per minimization step on a single processor

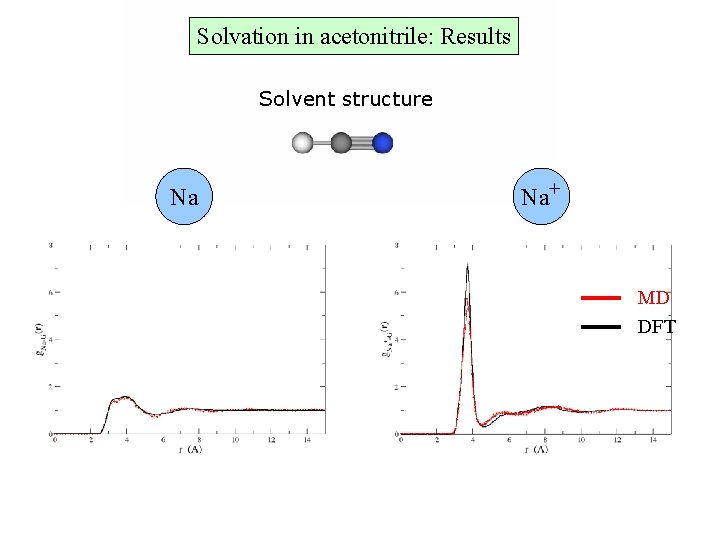
Solvation in acetonitrile: Results Solvent structure Na+ Na MD DFT

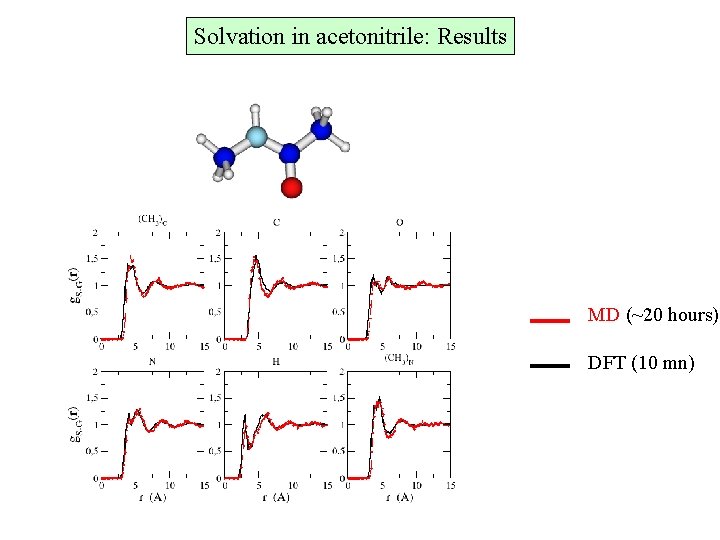
Solvation in acetonitrile: Results MD (~20 hours) DFT (10 mn)

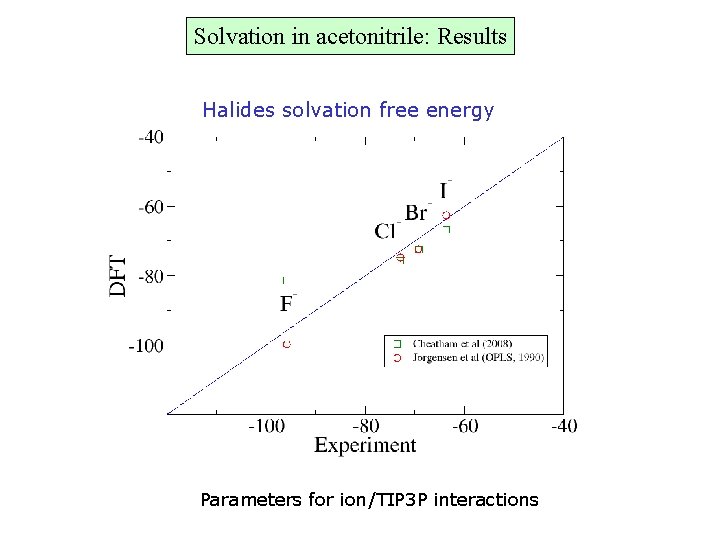
Solvation in acetonitrile: Results Halides solvation free energy Parameters for ion/TIP 3 P interactions

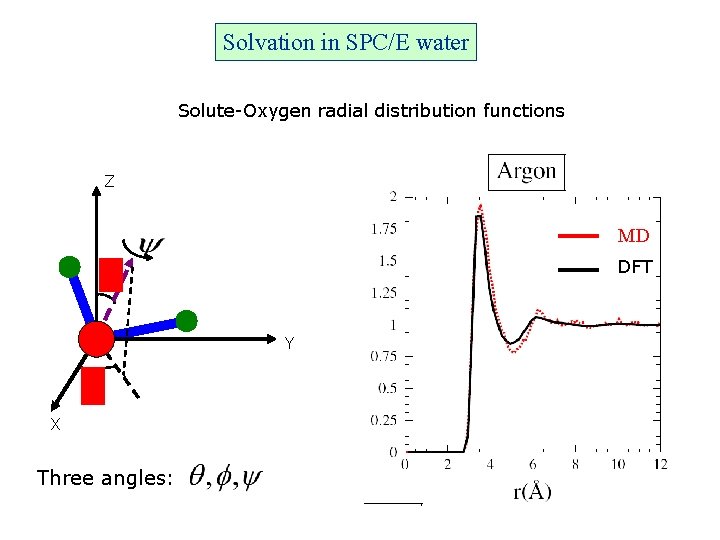
Solvation in SPC/E water Solute-Oxygen radial distribution functions Z MD DFT Y X Three angles:

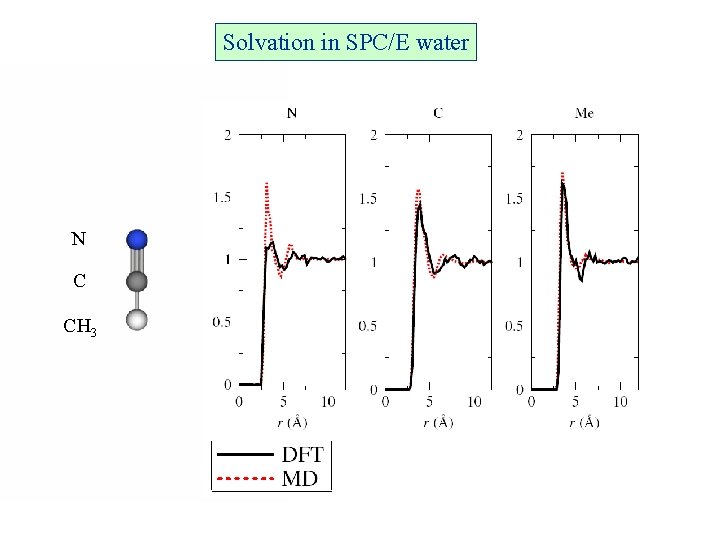
Solvation in SPC/E water N C CH 3

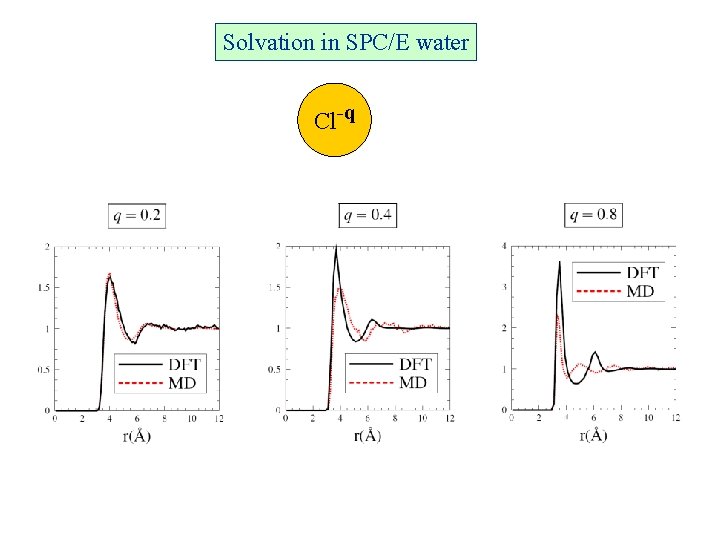
Solvation in SPC/E water Cl-q

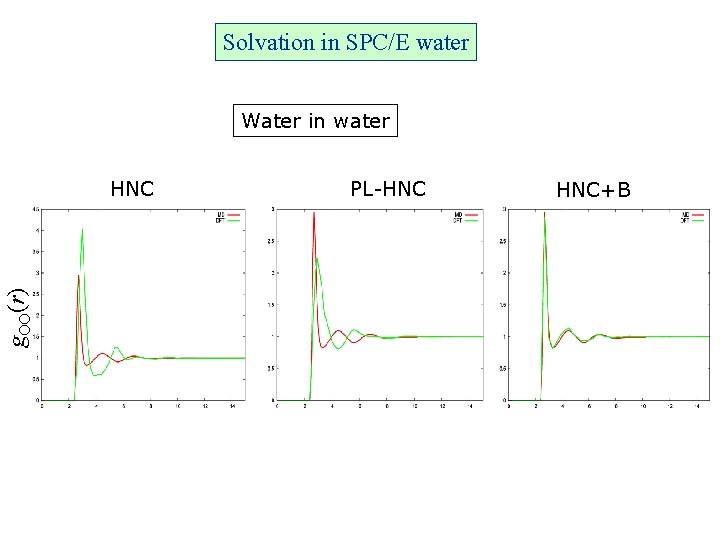
Solvation in SPC/E water Water in water g. OO(r) HNC PL-HNC HNC+B

Conclusion DFT • One can compute solvation free energies and microscopic solvation profiles using « classical » DFT • Solute dynamics can be described using CPMD-like techniques • For dipolar solvents, we presented a generic functional of • Direct correlation functions can be computed from MD simulations • For general solvents, one can use angular grids instead of rotational invariants expansion • BEYOND: -- Ionic solutions -- Solvent mixtures -- Biomolecule solvation or R. Ramirez et al, Phys. Rev E, 66, 2002 J. Phys. Chem. B 114, 2005 Chem. Phys. 2005 L. Gendre at al, Chem. Phys. Lett. S. Zhao et al, In prep.

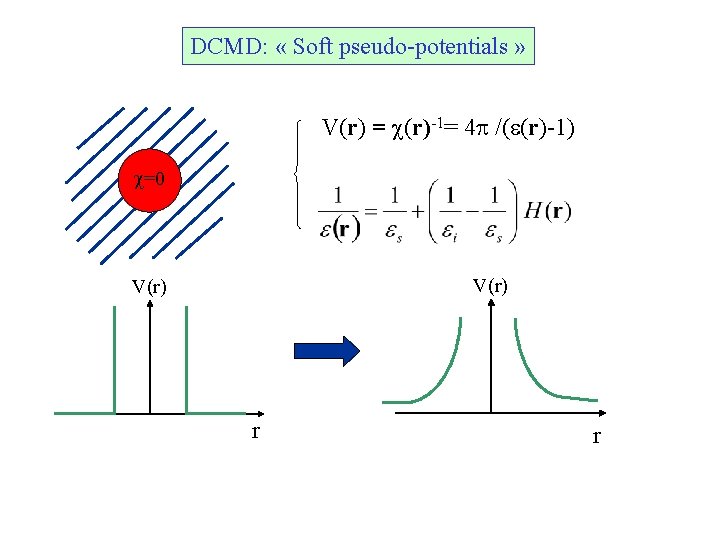
DCMD: « Soft pseudo-potentials » V(r) = c(r)-1= 4 p /(e(r)-1) c=0 V(r) r r

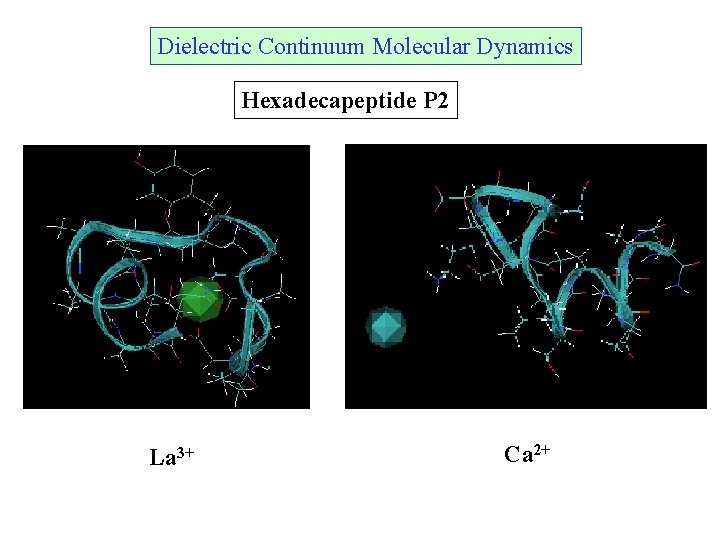
Dielectric Continuum Molecular Dynamics Hexadecapeptide P 2 La 3+ Ca 2+

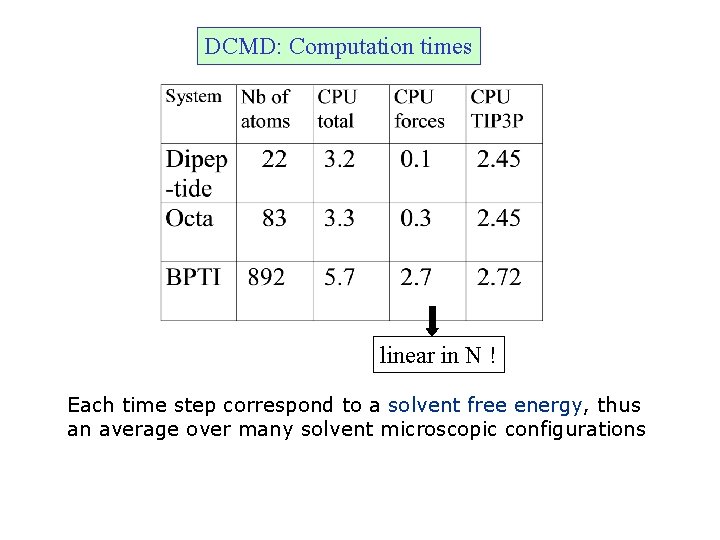
DCMD: Computation times linear in N ! Each time step correspond to a solvent free energy, thus an average over many solvent microscopic configurations