Classical Cryptosystems Shift Ciphers Caesar y xk mod

Classical Cryptosystems • • Shift Ciphers (Caesar) y= x+k (mod 26) Affine Ciphers y=ax+b (mod 26) Vigenere Ciphers codes=(02, 14, 03, 04, 18) Substitution Ciphers (26! Permutations) Sherlock Holmes P 27 (Visual Substitution) The Playfair and ADFG[V]X Ciphers Block Ciphers Pseudo. Random Number Generators

Shift Cipher y=x+k (mod 26) • attack XQQXZH (k=23 mod 26) • great ITGCV (k=2 mod 26) a b c d e f g h i j 00 01 02 03 04 05 06 07 08 09 k l m n o p q r s t 10 11 12 13 14 15 16 17 18 19 u v w x y z a b c d 20 21 22 23 24 25 00 01 02 03

Affine Cipher y=ax+b mod 26 • how are you QZNHOBXZD, (a, b)=(5, 7) • wo? ? er? u? NZUWBOGDK, (a, b)=(5, 7) gcd(a, 26)=1 is required Table for ax=1 mod 26 1(1) 7(15) 15( 7) 21(5) 3(9) 9( 3) 17(23) 23(17) 5(21) 11(19) 19(11) 25(25)

Frequencies of Letters in English a b c d e f g h i. 082. 015. 028. 043. 127. 022. 020. 061. 070 j k l m n o p q r. 002. 008. 040. 024. 067. 075. 019. 001. 060 s t u v w x y z. 063. 091. 028. 010. 023. 001. 020. 001

Vigenere Cipher The same letter need not be enciphered as the same letter Key: vector=(21, 4, 2, 19, 14, 17) h e r e i s h o wi t w o r k s v e c t o r v e c t C I TXWJCS YBHNJ VML Attacks according to the following information (1) The frequencies of letters in English A 0=[. 082, . 015, . 028, …, . 020, . 001] <A 0, A 0> is larger than <A 0, Aj>, j=1, 2, . . . , 25 (2) Key length (3) Digrams (e. g. , WX) or trigrams (e. g. , FHQ)

Sherlock Holmes A visual substitution (use a visual pattern to replace each English letter)

The Playfair p l a y f i r b c d e g h k m n o q s t u v w x z meet at the schoolhouse me et at th es ch ox ol ho us ex EG MN FQ QM KN BK SV VR GQ XN KU

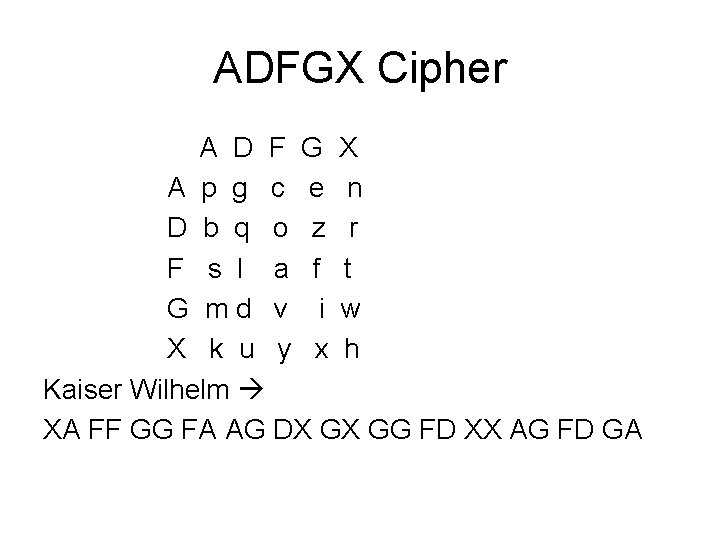
ADFGX Cipher A D F G X A p g c e n D b q o z r F s l a f t G md v i w X k u y x h Kaiser Wilhelm XA FF GG FA AG DX GX GG FD XX AG FD GA

Block Ciphers • Hill cipher, DES, AES, RSA, Electronic Codebook, Elliptic Curve cryptosystems • Find the inverse of A and B (mod 26) • A=3 4 inv-A=7 22 5 7 21 3 M = [1 2 3; 4 5 6; 11 9 8] inv-M=[22 5 1; 6 17 24; 15 13 1]

Hill Cipher • blockcipherx (1 11 14) (2 10 2) (8 15 7) (4 17 23) (1 11 14)M=(17 1 25) (mod 26) = RBZ (2 10 2)M =(12 20 4) (mod 26) = MUE blockcipher RBZMUEPYONOM

Binary Numbers and ASCII • ASCII – American Standard Code for Information Interchange • A=65=01000001 ~ Z=90=01011010 • a=97=01100001 ~ z=122=01111010 • [33~47] ! “ # $ % & ' ( ) * + , -. / • [48~64] 0 1 2 3 4 5 6 7 8 9 : ; ¡ = ¿ ? @

One-time Pads • By Gilbert Vernam and Joseph Mauborgne around 1918 • The key is a random sequence of 0’s and 1’s of the same length as the message. Once a key is used, it is discarded and never used again. • 00101001⊕ 10101100=10000101 • Used in “hot line” between USSR and US

Pseudo-random Bit Generation • Rand() based on a linear congruential generator xn=axn-1 + b (mod m) with gcd(a, m)=1, m=231 -1=2147483647 • x 0=seed, a=16847, b=314759 • Blum-Shub (BBS) bit generator • Select n=pq, the product of two primes • x 0=seed=x 2 (mod n), where gcd(x, n)=1 • xj=(xj-1)2 (mod n) and bj= xj ^ 1

Linear Feedback Shift Register (LFSR) Sequences (mod 2) • • • Plaintext 01000010 01011001 11110001 10111010 (x 1, x 2, x 3, x 4 , x 5)=(0, 1, 0, 0, 0) Xn+5 =Xn + X n+2 (mod 2) Xn+m=c 0 xn+c 1 xn+1+····+cm-1 xn+m-1 (mod 2) • Xn+31 =Xn + X n+3 (mod 2) has period 231 -1

Proposition • Let M be a matrix (mod 2) {x 1 x 2 x 3 ··· xm x 2 x 3 x 4 ··· xm+1 ︰ ︰ xm xm+1 xm+2 ··· x 2 m-1}={xj} If the sequence {xj} satisfies a linear recurrence of length less than m, then det(M)=0. Cinversely, if the sequence satisfies a linear recurrence of length m and det(M)=0, then the sequence also satisfies a linear recurrence of length than m.

• (plaintext) 1011001110001111 • (key) + 0100001001011001 • (ciphertext) 1111000111010110

Cryptanalysis • Suppose Xn+2=C 0 Xn+C 1 Xn+1

Cryptanalysis • If the linear recurrence of length is less than m, then

Irreducible Polynomial mod 2 • xn+m=c 0 xn+c 1 xn+1+····+cm-1 xn+m-1 (mod 2) • f(T)=Tm –cm-1 Tm-1 - ‥‥ - c 1 T 1 – c 0 • If f(T) is irreducible, then its period divides 2 m – 1, an interesting case is when 2 m – 1 is a prime (Mersenne primes) • 231 – 1 =2147483647 is a prime number • Further discuss this topic later

Enigma • A mechanical encryption device used by the Germans in World War II. • A rotor machine

Enigma

Schematic diagram of Enigma

Schematic diagram of Enigma

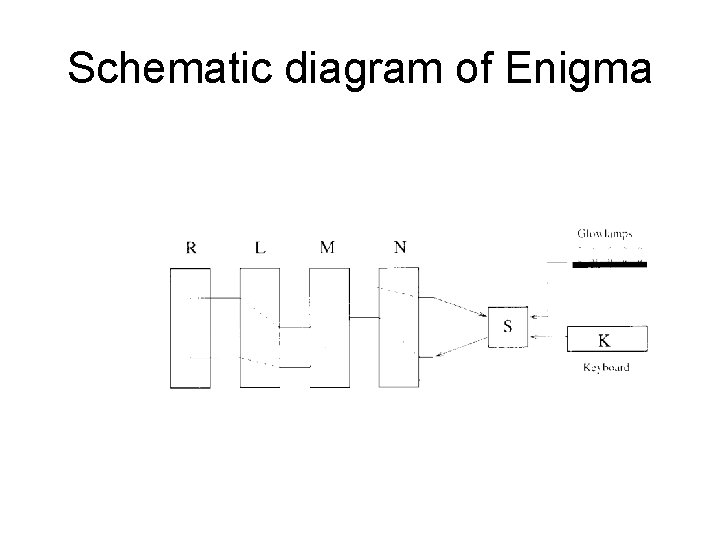
Schematic diagram of Enigma • • K: keyboard R: revering drum S: plugboard L, M, M: rotors

Single Rotor • • 26 substitution cipher A 1, A 27, A 53…. A 2, A 28, A 54…. Frequency analysis

Three Rotors • 26*26*26*6=105456 possibilities. • 100391791500 ways of interchanging six pairs of letters on the plugboard.

To Attack Enigma • A codebook containing the daily settings. • During a given day, every first letters in plaintexts is encrypted in the same substitution cipher.

To Attack Enigma • Message key: a sequence of three letters, for example, r, f, u. • rfurfu • Daily setting • Encrypting the message key • Reset

To Attack Enigma • • • dmqvbn vonpuy pucfmq AD=(dvpf. . )… AD=(dvpfkxgzyo)(eijmunqlht)(bc)(rw)(a)(s)

The Effect of the Plugboard • • AD has cycles of length 10, 2, 2, 1, 1. SADS-1 has cycles of length 10, 2, 2, 1, 1. The cycle lengths remain unchanged. Substitution cipher

Bletchley Park

Exercises • Problems from 2. 13 Exercises on p. 55~59 • Problems from 2. 14 Exercises • on p. 59~62