Classic Math Problems with Distance Rate and Time

Classic Math Problems with Distance, Rate, and Time

Today’s Learning Goal n n We will apply the steps to reading an algebra word problem to solving problems involving distance, rate, and time. We will learn how to use a picture and a rate-timedistance table to help us solve these problems.

Rate, Time, and Distance n In previous lessons, we worked a lot with rate, time, and distance. Consider the following two examples: A plane flies at 550 mph for 6 hours. D = 6*550 n n Jerome walks 2. 5 meters per second for 9 seconds. D = 9*2. 5 For each of these, how would you find the distance covered? Nice…multiply the rate times the time! We have seen that distance equals rate times time. In short, D = r*t.

Rate, Time, and Distance Problems n n n For rate, time, and distance problems, it is often convenient to draw a diagram because there are usually two moving objects. Consider the following example: One train leaves Chicago for Boston and at the same time another train leaves Boston for Chicago on the same track but traveling at different speeds. The sketch for this would look something like this: Train 1 n Train 2 Chicago Boston Notice that because the trains left at the same time, we drew the trains coming at each other.

Rate, Time, and Distance Problems n n Different problems will have different sketches that correspond to the direction and distance of each object that is moving. Consider this example: Mr. Nemuth leaves New York for a drive to Long Island. Later he returns to New York. What would the sketch of this look like? New York Long Island Because Mr. Nemuth traveled at different times, we did not draw his travel lines coming at each other.

Rate, Time, and Distance Problems n n Consider this example: Two planes leave New York at 10 am. One plane is heading for Europe and the other plane is heading in the opposite direction. What would the sketch of this look like? New York n Because the planes left at the same time, we drew the travel lines on the same line.

Rate, Time, and Distance Problems n n Consider this last example: One train leaves Los Angeles for Chicago at 40 mph. Two hours later, a second train leave Los Angeles for Chicago at 75 mph. What would the sketch of this look like? Los Angeles n Chicago (2 hours later) Chicago Again, because the trains left at different times, we did not draw the travel lines on the same line.

Rate, Time, and Distance Problems n n Now that we have seen how to draw diagrams for each type of problem, let’s look at a real problem: A car leaves San Francisco for Los Angeles traveling an average of 60 mph. At the same time, another car leaves Los Angeles for San Francisco traveling 50 mph. If it is 440 miles between San Francisco and Los Angeles, how long before the two cars meet? First, let’s draw a sketch of the movement in the problem. What will the sketch look like? San Francisco Car 1 Car 2 440 miles Los Angeles

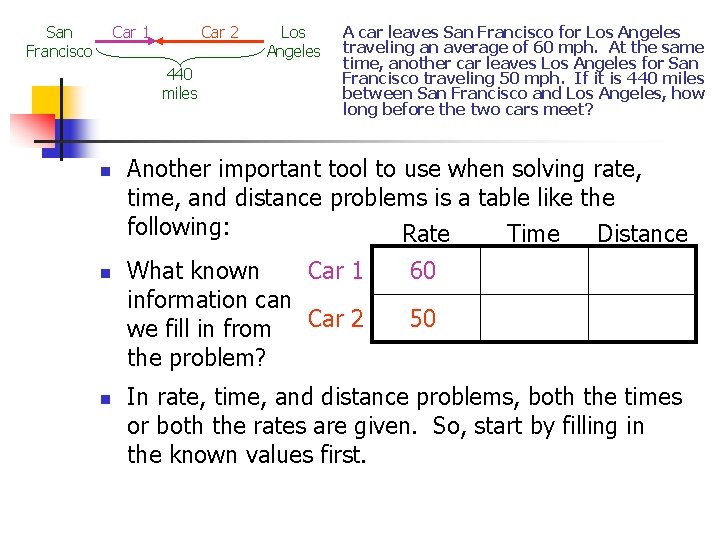
San Francisco Car 1 Car 2 440 miles n n n Los Angeles A car leaves San Francisco for Los Angeles traveling an average of 60 mph. At the same time, another car leaves Los Angeles for San Francisco traveling 50 mph. If it is 440 miles between San Francisco and Los Angeles, how long before the two cars meet? Another important tool to use when solving rate, time, and distance problems is a table like the following: Rate Distance Time What known Car 1 information can we fill in from Car 2 the problem? 60 50 In rate, time, and distance problems, both the times or both the rates are given. So, start by filling in the known values first.

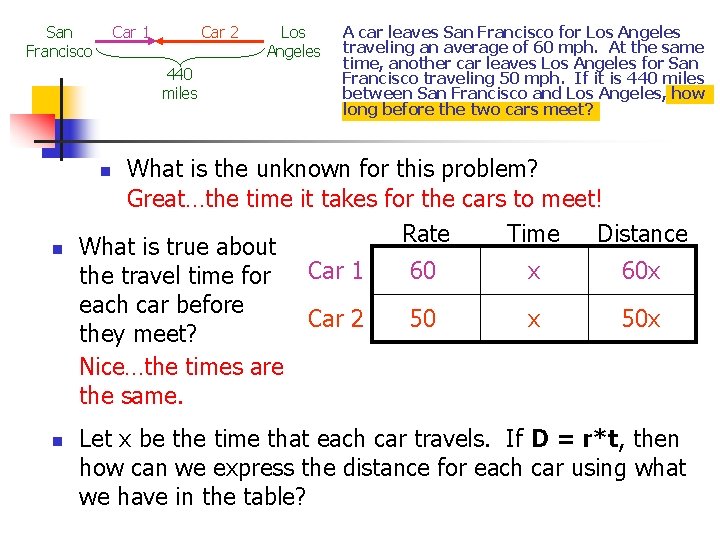
San Francisco Car 1 Car 2 440 miles Los Angeles A car leaves San Francisco for Los Angeles traveling an average of 60 mph. At the same time, another car leaves Los Angeles for San Francisco traveling 50 mph. If it is 440 miles between San Francisco and Los Angeles, how long before the two cars meet? What is the unknown for this problem? Great…the time it takes for the cars to meet! Rate Distance Time What is true about Car 1 60 x 60 x the travel time for each car before Car 2 50 x 50 x they meet? Nice…the times are the same. n n n Let x be the time that each car travels. If D = r*t, then how can we express the distance for each car using what we have in the table?

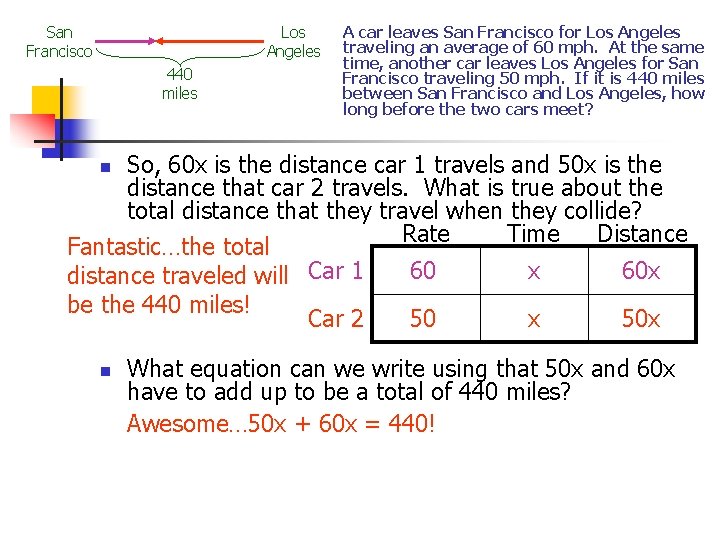
San Francisco 60 x Car 1 50 x 2 Car 440 miles Los Angeles A car leaves San Francisco for Los Angeles traveling an average of 60 mph. At the same time, another car leaves Los Angeles for San Francisco traveling 50 mph. If it is 440 miles between San Francisco and Los Angeles, how long before the two cars meet? So, 60 x is the distance car 1 travels and 50 x is the distance that car 2 travels. What is true about the total distance that they travel when they collide? Rate Distance Time Fantastic…the total 60 x 60 x distance traveled will Car 1 be the 440 miles! Car 2 50 x 50 x n n What equation can we write using that 50 x and 60 x have to add up to be a total of 440 miles? Awesome… 50 x + 60 x = 440!

San Francisco 60 x Car 1 50 x 2 Car 440 miles n n n Los Angeles A car leaves San Francisco for Los Angeles traveling an average of 60 mph. At the same time, another car leaves Los Angeles for San Francisco traveling 50 mph. If it is 440 miles between San Francisco and Los Angeles, how long before the two cars meet? Now that we have our equation, we can solve the problem. What would you do first? Yes…combine the x-terms 50 x + 60 x = 440 together! 110 x = 440 When we divide both 110 sides by 110, what is x=4 the x-value? What does the solution of x = 4 mean in terms of this situation? Super…after four hours, the two cars would have met!

Rate Time Distance Rate, Time, and Distance Problems n n n For rate, time, and distance problems, if it says that the two object leave at the same time or meet at the same time, then the times are both the same. For these problems, do not put anything in the distance box until all other information is filled in. The distance box can be filled in using the D = r*t relationship. Every rate, time, and distance problem has some kind of relationship between the distances. For the last problem, both distances added up to be the total of 440 miles. You have to watch for this relationship!

Rate, Time, and Distance Problems n n Let’s try another problem: Mr. Derbyshire makes a business trip from his house to Loganville in 2 hours. One hour later, he returns home in traffic at a rate 20 mph less than his rate going. If Mr. Derbyshire is gone a total of 6 hours, how fast did he travel on each leg of the trip? First, let’s draw a sketch of the movement in the problem. What will the sketch look like? House (1 hour later) Loganville

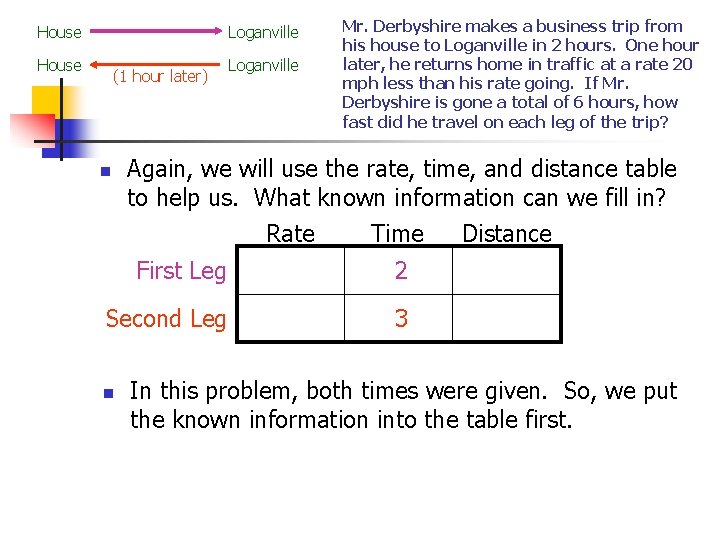
House Loganville House (1 hour later) n Loganville Mr. Derbyshire makes a business trip from his house to Loganville in 2 hours. One hour later, he returns home in traffic at a rate 20 mph less than his rate going. If Mr. Derbyshire is gone a total of 6 hours, how fast did he travel on each leg of the trip? Again, we will use the rate, time, and distance table to help us. What known information can we fill in? Rate Distance Time First Leg 2 Second Leg 3 n In this problem, both times were given. So, we put the known information into the table first.

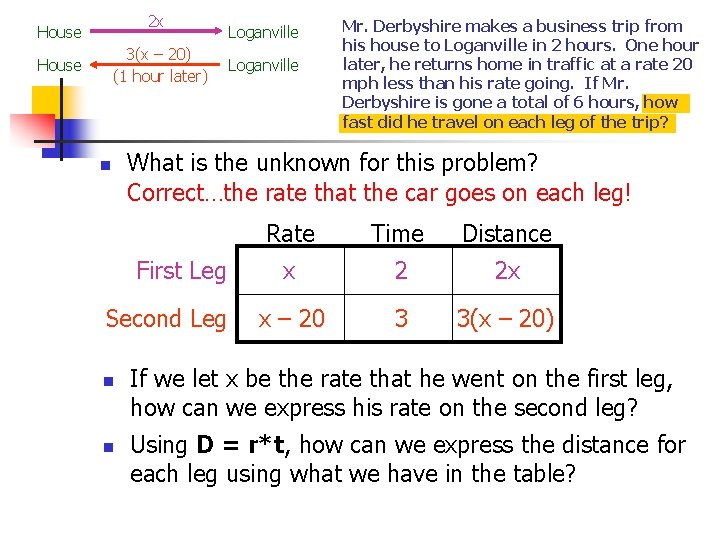
2 x House 3(x – 20) (1 hour later) House n Second Leg n Loganville Mr. Derbyshire makes a business trip from his house to Loganville in 2 hours. One hour later, he returns home in traffic at a rate 20 mph less than his rate going. If Mr. Derbyshire is gone a total of 6 hours, how fast did he travel on each leg of the trip? What is the unknown for this problem? Correct…the rate that the car goes on each leg! First Leg n Loganville Rate Time Distance x 2 2 x x – 20 3 3(x – 20) If we let x be the rate that he went on the first leg, how can we express his rate on the second leg? Using D = r*t, how can we express the distance for each leg using what we have in the table?

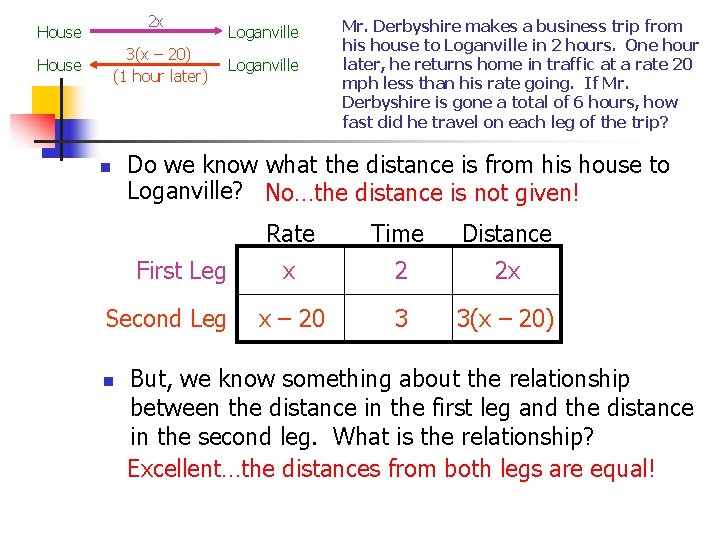
2 x House 3(x – 20) (1 hour later) House n Loganville Mr. Derbyshire makes a business trip from his house to Loganville in 2 hours. One hour later, he returns home in traffic at a rate 20 mph less than his rate going. If Mr. Derbyshire is gone a total of 6 hours, how fast did he travel on each leg of the trip? Do we know what the distance is from his house to Loganville? No…the distance is not given! First Leg Second Leg n Loganville Rate Time Distance x 2 2 x x – 20 3 3(x – 20) But, we know something about the relationship between the distance in the first leg and the distance in the second leg. What is the relationship? Excellent…the distances from both legs are equal!

2 x House 3(x – 20) (1 hour later) House n n Loganville Mr. Derbyshire makes a business trip from his house to Loganville in 2 hours. One hour later, he returns home in traffic at a rate 20 mph less than his rate going. If Mr. Derbyshire is gone a total of 6 hours, how fast did he travel on each leg of the trip? Because the distances are equal on both legs of the trip, what is the equation we can write? 2 x = 3(x – 20) Now, we just need to solve the equation. If we used the 2 x = 3 x – 60 -2 x distributive property first, what would be the resulting equation? 0 = x – 60 +60 If we subtracted 2 x from both 60 = x sides, what will be the resulting equation? What is the last step to solve the equation? Perfect…add 60 to both sides.

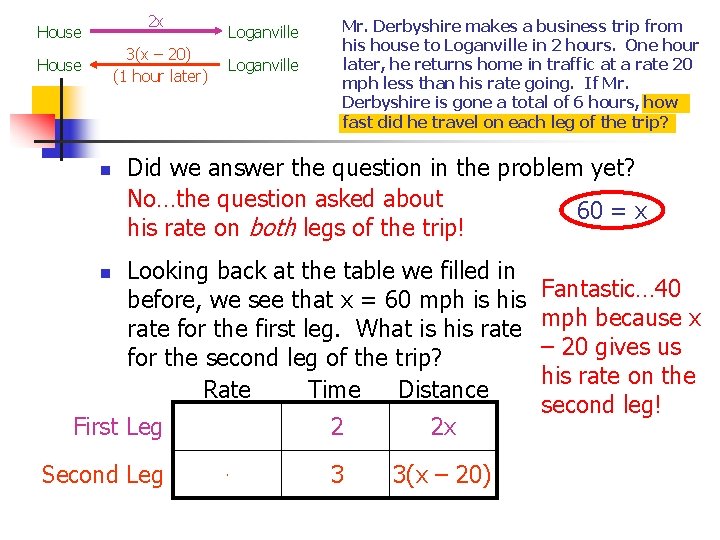
2 x House Loganville 3(x – 20) (1 hour later) House n n Loganville Mr. Derbyshire makes a business trip from his house to Loganville in 2 hours. One hour later, he returns home in traffic at a rate 20 mph less than his rate going. If Mr. Derbyshire is gone a total of 6 hours, how fast did he travel on each leg of the trip? Did we answer the question in the problem yet? No…the question asked about 60 = x his rate on both legs of the trip! Looking back at the table we filled in before, we see that x = 60 mph is his rate for the first leg. What is his rate for the second leg of the trip? Rate Distance Time First Leg Second Leg x 2 2 x x – 20 3 3(x – 20) Fantastic… 40 mph because x – 20 gives us his rate on the second leg!

Partner Work n You have 20 minutes to work on the following questions with your partner.

For those that finish early Solve the following problems: 1. Two planes leave New York at 10 am, one heading for Europe at 600 mph and one heading in the opposite direction at 150 mph (so it isn’t a jet). At what time will they be 900 miles apart? How far has each traveled? 2. A freight train starts from Los Angeles and heads for Chicago at 40 mph. Two hours later, a passenger train leaves the same station for Chicago traveling 60 mph. How long before the passenger train overtakes the freight train?

Big Ideas from Today’s Lesson n n With rate, time, and distance problems, usually both rates or both times are given in the problem. Use D = r*t to express the distances of each object as algebraic expressions. The relationship between the distances has to be discovered by you through reading the problem. Use a picture and the rate-time-distance table to help you solve the problem.

Homework n Complete Homework Worksheet.